Vuoden 2020 ylioppilaskokeet ja pientä vertailua vuoden 2021 tehtäviin

Tämä teksti on kovin myöhässä vuoden 2020 tehtävien osaamisanalyysin osalta. Tällä hidastelulla voitetaan onneksi se, että nyt vuoden 2020 ja 2021 tehtäviä voi hiukan vertailla keskenään. Tässä vaiheessa ei tietenkään vielä tiedetä miten 2021 kokeet ovat oikeasti menneet, mutta sehän ei estä etsimästä samankaltaisuuksia tehtävistä.

Tämän tekstin tarkoitus ei ole tarjota kaikenkattavaa analyysia, vaan enemmänkin highlighteja ylioppilaskoetehtävistä ja yksittäisiä havaintoja hyvin tai heikosti osatuista tehtävistä.

Tarkastellaan nyt vielä edellisen vuoden matematiikan ylioppilaskokeita, vaikka kevään 2021 kirjoituksetkin ovat jo ohi. Sekä kevään että syksyn 2020 kokeet olivat poikkeuksellisissa olosuhteissa. On hyvin hankala arvioida vaikuttivatko olosuhteet kokeiden tuloksiin, mutta joka tapauksessa karkeasti voi arvioida kevään pitkän matematiikan kokeen olleen hyvin hankala ja syksyn kokeen taas paljon leppoisampi. Lyhyessä kevään koe oli pistemääristä päätellen suurinpiirtein yhtä haastava kuin yleensäkin, ehkä hieman haastavampi, mutta syksyn koe osoittaui varsin haastavaksi.

Taustaa

Kevään 2019 pitkän matematiikan kokeet olivat olleet hankalat. Niiden jälkeen esimerkiksi MAOL oli todennut, että alakohdat olisivat hyviä, koska tällöin vaikeassakin tehtävässä kokelas voisi osoittaa osaamistaan vastaamalla edes alakohtaan. Lisäksi kokelas voisi näin päästä tehtävän kanssa vauhtiin. Kevään 2020 kokeessa olikin hankalissa tehtävissä alakohtia enemmän kuin keväällä 2019. Ehkäpä tämän vaikutuksesta tai sitten vain muuten tehtävien vaikeusasteen vuoksi kaikkein vaikeimmista tehtävistä tulikin enemmän pisteitä kuin keväällä 2019.

Kaikkien tehtävien pistekeskiarvot ovat oheisessa taulukossa:

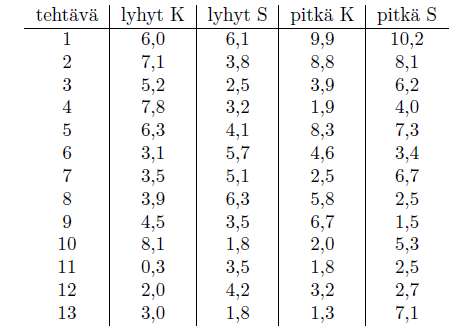
Kevään 2020 pitkän matematiikan kokeessa positiivista oli se, että helpoimmat tehtävät olivat antaneet melko paljon pisteitä. Keskitason tehtävissä pistemäärä jäi ehkä yleisesti ottaen hieman matalaksi, ja todennäköisyyslaskennassa (tehtävä 7) todella matalaksi. Vaikeimpien tehtävien keskiarvot eivät myöskään keväällä 2020 olleet huippuluokkaa.

Kevään 2019 vaikeimmiksi osoittautuivat tehtävät 12 ja 13. Tehtävän 12 pistekeskiarvo oli 0,4 ja tehtävän 13 0,9. Keväällä 2020 heikoimmat pistekeskiarvot olivat tehtävissä 13 (1,3) ja tehtävässä 11 (1,8). Tehtävässä 11 oli alakohtia, tehtävässä 13 puolestaan ei.

Näistä luvuista on noustu syksyllä 2020 selvästi: tällöin heikoiten osattiin huonon onnen lukuteorian tehtävää, jossa pistekeskiarvo oli 1,5 ja toiseksi heikoiten tehtävää 11, jossa pistekeskiarvo oli 2,5. Kaikkien muiden vaikeidenkin tehtävien pistekeskiarvo oli vähintään 2,5, tehtävän 13 peräti 7,1.

Lyhyessä matematiikassa keväällä 2020 ei tapahtunut mitään kovin ihmeellistä. Tehtävän 11 pistekeskiarvo jäi kovin pieneksi, mutta muita tehtäviä osattiin varsin hyvin. Sen sijaan syksyn 2020 pisteet ovat karua luettavaa. Parhaiten on osattu tehtävää 1. Siitä on saatu keskimäärin 6,1 pistettä. B1-osion tehtäväkohtaiset keskiarvot ovat kohtuullisia, joskin jonkin verran matalia. Valitettavasti se ei riitä pitämään kokonaispisteitä tyypillisellä tasolla, jos A-osiosta on tullut kovin vähän pisteitä.

Lopulta kuitenkin ehkä mielenkiintoisinta suurten joukkojen osaamisen kannalta ei ole niinkään vertailla miten eri kokeiden B2-osia on osattu vaan enemmänkin miten niitä perustehtäviä on osattu.

Todennäköisyyslaskenta pitkässä matematiikassa

Keväällä 2020 pitkän matematiikan kokeessa oli todennäköisyyslaskennan tehtävä B1-osiossa:

Tehtävä. Yatzy-noppapelissä pelaaja heittää viittä noppaa. Tutkitaan tarkemmin heittoja, joiden tuloksena saadaan täyskäsi tai neliluku yhdellä viiden nopan heitolla. Täyskädellä tarkoitetaan tulosta, jossa yksi silmäluku esiintyy kolme kertaa ja joku toinen silmäluku kaksi kertaa. Neliluvussa esiintyy neljä samaa silmälukua ja yksi muu silmäluku.

1. Määritä todennäköisyys sille, että saadaan täyskäsi, jossa esiintyy kolme kuutosta ja kaksi viitosta. (3 p.)

2. Määritä todennäköisyys sille, että saadaan täyskäsi. (6 p.)

3. Määritä todennäköisyys sille, että saadaan neliluku. (3 p.)

Tämä tehtävä oli B1-osiossa ja tätä tehtävää yritti ratkaista lähes 8800 kokelasta. Tehtävän pistekeskiarvo oli 2,5 pistettä. Ongelmaksi osoittautuivat binomikertoimet. Siinä missä esimerkiksi ensimmäinen kohta olisi pitänyt ratkaista näin: Tarvitaan kolme kuutosta ja kaksi viitosta. Lasketaan tavat miten kuutoset voivat sijoittua viiteen noppaan. Tämä voi tapahtua $\binom{5}{3}=10$ tavalla. Kuutosen todennäköisyys on $\frac{1}{6}$, joka on myös viitosen todennäköisyys, joten kysytty todennäköisyys on $\frac{10}{6^5}=\frac{5}{3888}$. Hyvin monessa ratkaisussa oli unohdettu binomikerroin, jolloin kolmen kuutosen ja kahden viitosen todennäköisyys oli sama kuin olisi ollut esimerkiksi viiden kuutosen todennäköisyys. Sama virhe toistui kaikissa kohdissa. Tämä ei tietenkään ollut ainoa virhe ratkaisuissa, mutta hyvin tyypillinen esimerkki.

Syksyllä 2020 oli täsmälleen samassa kohdassa koetta todennäköisyyslaskennan tehtävä:

Tehtävä. Pitkäaikaisten tilastojen perusteella erään koripalloilijan todennäköisyys heittää pallo vapaaheitolla koriin on $p$ ($0 \leq p \leq 1$). Rautahermoisena pelaajana hänen heittojensa onnistumistodennäköisyydet ovat riippumattomia aikaisempien heittojen tuloksista ja pelitilanteesta.

Eräässä ottelussa kyseinen pelaaja saa kaksi vapaaheittoa, jotka on heitettävä peräkkäin. Merkitään

1. Laske $P ( 2 )$ , kun $p = 0 \mathrm{,} 82$ . (3 p.)

2. Määritä $P ( 2 )$ , $P ( 1 )$ ja $P ( 0 )$ todennäköisyyden $p$ avulla lausuttuina. (6 p.)

3. Millä todennäköisyyden $p$ arvoilla on $P ( 1 ) = P ( 2 )$ ? (3 p.)

Tämän tehtävän keskiarvo oli peräti 6,7, eli kaiken kaikkiaan tätä oli osattu melko hyvin. Melko tyypillinen virhe oli unohtaa todennäköisyytta $P(1)$ määritettäessä, että kumpikin tapaus on mahdollinen: ensimmäinen koriin, toinen ei tai toinen koriin, ensimmäinen ei. Tästä lähti lopulta hyvin vähän pisteitä, ja ennen kaikkea kolmannen kohdan saattoi ratkaista täysien pisteiden arvoisesti väärälläkin todennäköisyydellä kunhan tehtävän luonne säilyi.

Vaihtoehtojen unohtaminen on hyvin inhimillinen virhe. Se käytännössän toistui sekä keväällä että syksyllä. Se myös sopii mainiosti yhteen sen kanssa, että välillä jopa matematiikkaa opiskelleet ihmiset väittävät, että kaksilapsisessa perheessä on kolme yhtä todennäköistä tapausta: kaksi tyttöä, kaksi poikaa, yksi tyttö ja yksi poika, jolloin siis unohdetaan täysin se, että tyttö ja poika voivat syntyä kummassa tahansa järjestyksessä.

Kuvien piirtäminen ja pienten erikoistapausten miettiminen huolella läpi ei olisi haitaksi koetilanteessa tai koskaan muulloinkaan todennäköisyyslaskentaa harrastaessa.

Alkuluvut osana kokonaislukuja – tai sitten ei

Syksyn 2020 pitkän matematiikan kokeessa heikoin tehtäväkohtainen pistekeskiarvo osui B1-osion lukuteorian tehtävälle:

Tehtävä. Osoita lukua $1\, 000\, 001 ! + 2$ käyttämällä, että on olemassa miljoona peräkkäistä kokonaislukua, joista yksikään ei ole alkuluku.

Tehtävän ratkaisu on varsin suoraviivainen: Koska $1\, 000\, 001 !$ on jaollinen luvuilla $2,3,\dots ,1\, 000\, 001$, on luku $1\, 000\, 001!+k$ jaollinen luvulla $k$, kun $2\leq k \leq 1\, 000\, 001$ ja $k$ on kokonaisluku. Siispä $1\, 000\, 001!+k$ ei voi olla alkuluku. Koska mahdollisia luvun $k$ arvoja on miljoona, on löydetty miljoona peräkkäistä lukua, joista mikään ei voi olla alkuluku.

Tätä tehtävää ei edes yrittänyt kovin moni kokelas. Osa syystä saattoi olla se, että tässä tehtävässä kaavaeditori ei toiminut. Surullista tietysti on, että kaavaeditori ei toiminut, mutta onneksi ongelma tuli juuri tämän tehtävän kanssa. Ratkaisun pystyi kirjoittamaan ilman kaavaeditoria paljon sujuvammin kuin moneen muuhun tehtävään.

Ratkaisuissa hieman hämmensi se, että tätä oli selvästi lähdetty ratkomaan tietämättä mikä on alkuluku (tai onko alkuluku edes kokonaisluku) tai mikä on kertoma.

Ymmärrys algoritmeista

Syksyn 2020 pitkän matematiikan tehtävää 13 osattiin yllättävän hyvin. Tehtävä ei sinänsä ollut erityisen vaikea, mutta varmasti tyypillisestä tai totutusta poikkeava:

Tehtävä. Tason monikulmio voidaan esittää järjestettynä listana $[(x_1, y_1) , \dots , ( x_n , y_n )]$ kärkipisteitä niin, että monikulmion reuna saadaan yhdistämällä peräkkäiset kärkipisteet sekä ensimmäinen ja viimeinen kärkipiste janoilla. Oletetaan, että monikulmion reuna ei leikkaa itseään. Käytössä on menetelmä, joka laskee annetun kolmion pinta-alan, ja se halutaan yleistää monikulmioille.

1. Piirrä tarkka kuva monikulmiosta, joka vastaa listaa $[ ( 2 , 2 ) , ( 3 , -1 ) , ( 5 , 2 ) , ( 7 , 3 ) , ( 4 , 6 ) ]$. (2 p.)

2. Terje ehdottaa seuraavaa algoritmia monikulmion pinta-alan määrittämiseksi:

i Valitaan satunnainen kärkipiste.

ii Piirretään siitä janat kaikkiin muihin kärkiin, jolloin muodostuu joukko kolmioita.

iii Lasketaan näiden kolmioiden pinta-alat yhteen.

Anna esimerkki monikulmiosta, jolle algoritmi antaa väärän pinta-alan ja toinen esimerkki sellaisesta monikulmioista, jonka pinta-alan algoritmi antaa oikein. (5 p.)

3. Aale ehdottaa seuraavaa toimintaohjetta monikulmion pinta-alan määrittämiseksi:

i Jaetaan monikulmio kolmioihin yhdistämällä sopivasti kärkipisteitä.

ii Lasketaan yhteen näiden kolmioiden pinta-alat.

Mitä puutteita Aalen ehdotuksessa on, eli miksi tämä ei ole algoritmi? (5 p.)

Kahta ensimmäistä kohtaa osattiin todella hyvin. Viimeinen kysymys oli haastavin ja siinä horjumista olikin entinen. Osa osasi täsmällisesti selittää miksi kyseessä ei ole algoritmi, mutta myös paljon näkyi virheellisiä yritelmiä.

Algoritmista ajattelua on mitattu pitkän matematiikan kokeissa muulloinkin: Kevään 2020 kokeessa tehtävänä 12 oli selvittää lukuja, joiden geometrinen keskiarvo on kokonaisluku:

Tehtävä. Kahden positiivisen luvun $a$ ja $b$ geometrinen keskiarvo on $\sqrt{ab}$.

1. Anna esimerkki välin 2–100 kahdesta eri kokonaisluvusta $a$ ja $b$, joille $\sqrt{ab}$ on kokonaisluku. (3 p.)

2. Satunnaislukugeneraattori arpoo toisistaan riippumatta kaksi kokonaislukua väliltä 1–100 niin, että jokaisen luvun todennäköisyys on 1-100 . Mikä on todennäköisyys sille, että arvottujen lukujen geometrinen keskiarvo on kokonaisluku? Voit laskea tapahtuman klassisen todennäköisyyden tarkasti tai esittää sille simulointiin perustuvan arvion. (9 p.)

Keväällä 2021 taas piti simuloida pinta-alaa Monte Carlon algoritmilla, jonka saattoi toteuttaa taulukkolaskennalla tai vaikka pseudokoodina.

Syksyn 2020 tehtävä oli näistä jossain mielessä teoreettisin: siinä selvitettiin hahmottaako kokelas mikä oikeasti on algoritmi tai millaisia algoritmit ovat. Kevään 2020 tehtävä oli periaatteessa ratkaistavissa klassisesti todennäköisyyslaskennalla, mutta tämä ratkaisu on melkoisen työläs. Vähemmällä pääsee taulukkolaskennan kanssa. Tämän kevään tehtävä pyytää suoraan konkreettista algoritmia, mutta sen toteuttamistapoja on useita. Esimerkiksi taulukkolaskennalla se on (minun mielestäni) helpompi kuin geometrisen keskiarvon tehtävä, sillä se vaati vain pisteiden arpomisen taulukkolaskentaohjelman valmiilla kommennolla, suuruusehdon tarkistamisen ja kirjanpidon ehdon toteuttavista pisteistä.

Lyhyen matematiikan yhtälöt ja peruslaskutoimitukset

Lyhyen matematiikan kokeen A-osiossa mitattiin sekä keväällä että syksyllä 2020 peruslaskutoimitustaitoja. Keväällä painopiste oli polynomilausekkeiden sievennyksissä ja murtolukulaskutoimituksissa, syksyllä puolestaan yhtälöissä. Kevään tehtävät menivät selvästi paremmin kuin syksyn tehtävät. Keväällä 1. tehtävän pistekeskiarvo oli 6,0, ja toisen tehtävän 7,1, kun taas syksyllä 2. tehtävän pistekeskiarvo oli 3,8. Syksyn 2. tehtävä näytti tältä:

Tehtävä. Ratkaise seuraavat yhtälöt. Anna vastausten likiarvot kahden desimaalin tarkkuudella.

1. $x^2= 7$ (3 p.)

2. $7x^5+ 2 = -3 x^5+4$ (3 p.)

3. $(3x )^3 \cdot 3^4=3^{11}$ (3 p.)

4. $13^x= 147$ (3 p.)

Tätä tehtävää kritisoitiin siitä, että toisen kohdan ratkaiseminen vaatii viidennen juuren ottamista ja että kokeessa funktiolaskimesta ei saa viidettä juurta kulkematta murtopotenssien kautta. Myös editorissa olleesta ongelmasta viidennen juuren kirjoittamisen kanssa tuli palautetta. Yksittäinen palaute tuli myös siitä, että tarkkojen arvojen olisi pitänyt riittää.

Tässä tehtävässä olisin todella onnellinen, jos ainoat ongelmat olisivat ylläolevat kritiikkiä saaneet. Käytännössä kuitenkin hyvin moni ratkaisuyritys toiseen alakohtaan kaatui jo paljon ennen viidennen juuren ottamista. Samanlaiset termit usein yritettiin yhdistää, mutta lopputuloksen aste ei aina ollut se mitä sen olisi pitänyt olla, vaan mahdollisestei myös eksponentit laskettiin yhteen tai tehtiin muuta vastaavaa. Tämä kuvaamani ongelma ei varmasti ole yllätys kovinkaan monelle. Hieman häiritsevämpää on ehkä se, että ensimmäisessä tehtävässä yllättävän yleinen vastaus oli 3,5, eli neliöjuuri oli samaistettu kahdella jakamiseen. Hyvin loogisesti sama ongelma näkyi myös viimeisessä kohdassa: logaritmi oli korvautunut jakolaskulla, eli viimeisen kohdan $x$ ei ollutkaan $x=\frac{\lg 147}{\lg 13}\approx 1\mathrm{,}95$ vaan $x\approx 11\mathrm{,}31$.

Vastaavia asioita A-osassa on jälleen: keväällä 2021 tehtävässä 1 on peruslaskutoimituksia, tehtävässä 3 annetusta yhtälöstä tietyn tuntemattoman ratkaisemista muiden avulla ja tehtävässä 4 pitää tunnistaa suoria ja niiden yhtälöitä.

Keväällä 2020 A-osion neljättä tehtävää oli osattu oikein hyvin: pistekeskiarvo oli parempi kuin missään muussa A-osion tehtävässä. Tehtävä oli seuraava:

Tehtävä. Nations League -jalkapalloturnaus järjestettiin ensimmäisen kerran vuonna 2018. Turnauksessa pelataan seuraavien sääntöjen mukaan:

• Joukkueet on jaettu neljään liigaan: A, B, C ja D.
• Molemmissa liigoissa A ja B on 12 joukkuetta, jotka on jaettu neljään kolmen joukkueen lohkoon.
• Molemmissa liigoissa C ja D on 15 joukkuetta, jotka on jaettu yhteen kolmen joukkueen ja kolmeen neljän joukkueen lohkoon.
• Jokaisessa lohkossa kukin joukkue pelaa lohkon kaikkia muita joukkueita vastaan kaksi kertaa: yhden kotipelin ja yhden vieraspelin.
• Liigan A neljä lohkovoittajaa pelaavat lopputurnauksen, jossa on kaksi välieräottelua, yksi pronssiottelu sekä loppuottelu.

Kuinka monta ottelua pelataan yhdessä Nations League -turnauksessa?

Tämä tehtävä ei ollut miellyttävin mahdollinen sensoroida. Monessa ratkaisussa oli paljon hyvää, mutta selitysten aste vaihteli huomattavasti, lisäksi oikeisiin johtopäätöksiin saattoi päästä hyvin vaihtelevilla tavoilla, mikä tehtävän kannalta on hyvä, mutta tarkoittaa usein sitä, että sensorointi voi olla hyvinkin hidasta varsinkin hieman pielessä olevien tai hieman puutteellisten ratkaisujen kanssa.

Hyvin positiivista tämän osaamisessa on se, että tehtävän ratkaiseminen vaati tiettyjen kombinaatioiden lukumäärien laskemista ja sen jälkeen yhdistelyä. Tämä kombinatorinen laskeminen osattiin melko hyvin. Tämä tuo ainakin minulle toivoa, sillä kombinatoriikka ja todennäköisyyslaskenta liittyvät läheisesti yhteen. Näin konkreettisessa tehtävässä vaihtoehtojen laskeminen selvästi hallittiin varsin hyvin.

Neuleyritys ja ALV:n maksaminen

Lyhyen matematiikan kokeessa keväällä 2020 tehtävässä 10 annettiin taulukko aloittavan neuleyrityksen kuluista ja kysyttiin seuraavia asioita:

Tehtävä. Naapurukset Pauli ja Johanna päättävät perustaa lasten neuleita valmistavan yrityksen.

1. Yritys myy neuleita 70 euron kappalehinnalla. Kuinka monta tilausta tarvitaan kuukaudessa, jotta tulot kattavat taulukossa 10. A luetellut kulut? (4 p.)

2. Pauli ja Johanna miettivät, että yrityksen olisi hyvä tehdä voittoa, ja tuumaavat, että tähän voisi päästä, jos kuukausittain valmistetaan ja myydään 100 neuletta. Riittävätkö kuukauden tarpeisiin varatut langat tähän, kun merinovillalanka maksaa 39 euroa kilolta ja yhteen neulepaitaan tarvitaan 250 grammaa lankaa? (4 p.)

3. Aloittelevina yrittäjinä Paulilta ja Johannalta on jäänyt laskuissaan arvonlisävero sekä lomat huomioimatta. Kerro, miten näiden seikkojen ottaminen huomioon vaikuttaa siihen, kuinka paljon myyntituloja yritys tarvitsee ollakseen kannattava. Tietoa arvonlisäveron laskemisesta löytyy tekstistä 10. B. (4 p.)

Tehtävän pistekeskiarvo on oikein hyvä: 8,1, eli korkein koko kokeessa. Ensimmäistä kahta kohtaa osattiinkin todella hyvin. Viimeisessä kohdassa selitysten taso oli melko vaihteleva. Tämä ei ole yllättävää, sillä perustelut, analysoinnit ja ilmiöiden selitykset ovat usein haastavia. Sen sijaan hieman yllättäviä olivat melko yleiset vastaukset, joissa kerrottiin ALV:n unohtamisen itse asiassa parantavan yrityksen taloustilannetta, ja tämä perusteltiin sillä, että ALV maksetaan yritykselle.

Pohdiskelemaan pääsi B2-osiossa sekä syksyllä 2020 että jälleen keväällä 2021. Syksyllä 2020 piti antaa esimerkki todellisesta tilanteesta, jossa kahdella muuttujalla ei ole syy-yhteyttä, mutta ne kuitenkin korreloivat selvästi keskenään. Keväällä 2021 tehtävässä 11 kirjaviisauteen kyllästynyt dosentti myy kirjansa pois ja yrittää kahdella eri menetelmällä arvioida kirjojensa määrää. Näistä arviointimenetelmistä pitäisi perustellen valita parempi. Kevään 2021 tehtävässä 12 taas pääsi miettimään mitkä tekijät lopulta vaikuttavat asunnon kokonaiskustannuksiin.

B1-osio syksyn kokeessa

Vaikka syksyn lyhyen matematiikan koe yleisesti ottaen meni selvästi heikommin kuin yleensä, B1-osiota osattiin varsin hyvin, tai ainakin pistekeskiarvoista päätellen paremmin kuin keväällä. Pistekeskiarvot eivät tietenkään yksinään kerro koko totuutta, vaan myös ratkaisijoiden määrä tulisi huomioida paremman kokonaiskuvan saavuttamiseksi. Positiivista joka tapauksessa on se, että rekursiivisten jonojen tehtävän 8 pistekeskiarvo oli yli 6, ja se oli itse asiassa koko kokeen korkein tehtäväkohtainen keskiarvo. Tämä on ehkä hieman yllättävää, sillä lukujonojen oppimiseen liittyvistä hankaluuksista kuulee melko usein. Tehtävän toisessa alakohdassa oli peräti kaksi lukujonoa, jotka oli määritelty toistensa avulla, eli kyseessä ei missään nimessä ollut ihan perustehtävä:

Tehtävä.

1. Säästötilin saldolle maksetaan vuosittain $2%$ nettokorkoa, ja sen jälkeen tilille talletetaan $100$ euroa. Tilin saldoa $a_n$ voidaan mallintaa rekursiokaavalla \[a_{n + 1} = 1 \mathrm{,} 02 a_n + 100 ,\quad n \geq 1.\] Alkuarvona on $a_1 = 1000$. Laske $a_5$ eli saldo neljän vuoden jälkeen. (6 p.)

2. Tutkijat ovat mallintaneet korppipopulaation kokoa seuraavien rekursiokaavojen avulla: \[p_{n + 1} = 0 \mathrm{,} 95 p_n + 0 \mathrm{,} 02 e_n ,\]\[e_{n + 1} = p_n + e_n ( 1 -0 \mathrm{,} 01 e_n ) ,\]missä $p_n$ on pesivien korppien lukumäärä ja $e_n$ on ei-pesivien korppien lukumäärä vuonna $n \geq 1$. Alkuarvot ovat $p_1 = 12$ ja $e_1 = 23$ . Laske $p_2$ ja $e_3$. (6 p.)

Ensimmäistä kohtaa osattiin todella hyvin. Jonkin verran laskettiin väärän vuoden saldoa tai tehtiin pieniä huolimattomuusvirheitä. Toisessa kohdassa alaindeksit tuntuivat aiheuttavan hämmennystä. Moni sai tehtävän tehtyä oikein hyvin, mutta moni tuntui myös ottavan alaindeksit käyttöön jollain muulla kuin tarkoitetulla tavalla, esimerkiksi siis niin, että vaikkapa luvusta $p_{n+1}$ tulikin luku $p_n+1$ (eikä näyttänyt siltä, että kyseessä olisi vain tekninen ongelma indeksien kirjoittamisen kanssa). Kuriositeettina mainittakoon, että vuoden 2021 keväällä lyhyessä matikassa ei ollut lukujonotehtäviä. Pitkässä niitä sen sijaan oli.

Minut B1-osion pistejakuma yllätti, sillä olisin itse kuvitellut sekä maankäyttötehtävän (tehtävä 5) että hammastahnatehtävän (tehtävä 7) olevan huomattavasti helpompia kuin mitä ne olivat. Hammastahnatehtävä oli seuraava:

Tehtävä. Hammastahnatuubissa on 90 ml tahnaa, ja sen pyöreän suuaukon halkaisija on 6 mm. Riittääkö yksi hammastahnatuubi nelihenkisessä perheessä kolmen kuukauden käyttöön, kun jokainen perheenjäsen pesee hampaansa aamulla ja illalla ja pursottaa 5 mm tahnaa hammasharjaansa jokaisella pesukerralla?

Jos tätä vertaa esimerkiksi parin vuoden takaiseen maitopurkkiin (keskiarvo 7,6) tai puunrungon mallinnukseen (keskiarvo 3,9), näkisin, että tämä on lähempänä maitopurkkia kuin puuta. Lopulta kyse nimittäin ei ole muusta kuin hyvin pitkän ja hyvin kapean sylinterin tilavuuden määrittämisestä, joskin ehkä tehtävän asetelma teki tämän hahmottamisen tavallista hankalammaksi. Valitettavan monessa ratkaisussa nimittäin unohdettiin, että hammastahnaa käytetään kerrallaan kolmiulotteinen palanen, eikä kyseessä ole metreittäin myytävä tuote. Tämä virhe ehkä sopii yhteen syksyn 2019 kuorotehtävän kanssa samassa kokonaisuudessa olleisiin muihin alakohtiin, eli lounasperunoihin ja marmeladipaloihin: niidenkin koon vertailussa dimensiot unohtuivat usein, ja vertailu suoritettiin lineaarisesti.

Tämän kevään 2021 kokeessa kolmiulotteisen kappaleen tilavuus tarvitsi laskea vain tehtävässä, jossa maksimoidaan pahvista tehtävän laatikon kokoa. Ihan samanlaista kolmiulotteisen geometrian tehtävää ei tällä kertaa siis ollut.

Yhteenveto

On hyvin hankala sanoa onko syksyn 2020 koetulokset pitkän matematiikan kohdalla onnekas ja lyhyen matematiikan kohdalla onneton sattuma. Olosuhteet eivät olleet tavalliset, populaatiot ovat syksyisin pieniä, eli tulkinnoissa on normaalia korkeampi virhemahdollisuus. Tästä huolimatta päätän iloita siitä, että pitkän matematiikan koe osattiin hyvin ja ehkä hieman epäloogisesti toivoa, että lyhyen matematiikan kohdalla oli vain yksittäinen sattuma.