Värit, Sierpinski ja Pascal
Matematiikka on siitä ihmeellistä, että se paljastaa yhteisiä rakennepiirteitä näennäisesti erilaisistakin kohteista. Tässä jutussa esillä ovat värien yhteenlasku, kolmiofraktaali ja binomin potenssit.
Solmu-artikkelissaan [1] Saara Lehto esittelee neliöistä muodostuvan tasakylkistä kolmiota muistuttavan kuvion (kuva 1). Kunkin pikkuneliön väri määräytyy niin, että kyljillä olevat neliöt ovat sinisiä ja muiden väri määräytyy kahden edellisellä rivillä nurkittain olevan neliön perusteella. Jos ne ovat samanväriset, niin alemman neliön väriksi tulee punainen. Jos taas eriväriset, niin sininen. Tämä voidaan esittää myös värien yhteenlaskutauluna (kuva 1, oikea ylänurkka). Kahden värillisen neliön välissä on aina erottimena valkoinen neliö. Kuviosta alkaa hahmottua vähitellen sisäinen rakenne.

Sierpinskin kolmio
Samantapainen kuvio voidaan tuottaa myös geometrisin keinoin [2]. Poistetaan kolmiosta pienempi kolmio, jonka kärkipisteinä ovat kolmion sivujen keskipisteet (kuva 2). Jäljelle jäävien pikkukolmioiden kanssa toimitaan samoin yhä uudestaan. Jo kahden poistokierroksen jälkeen saadaan edellä olevaa, pikkuneliöistä muodostuvaa kuviota muistuttava hahmo (kuva 2, toinen osakuva oikealta).
Kun tätä jatketaan rajatta, jäljellä ei ole pienenpientäkään kolmiota. Kuvion pinta-ala on nolla, mutta kuitenkaan kuvio ei ole kokonaan kadonnut. Siitä on jäljellä tavallaan äärettömän pitkä viiva äärellisessä alueessa. Se ei siis ole enää kaksiulotteinen kuvio, mutta ei toisaalta yksiulotteinen viivakaan, vaan jotain niiden väliltä. Kuvio on fraktaali: Sierpinskin kolmio. Sen fraktaalidimensio on noin 1,6. Fraktaaleilla on se ominaisuus, että ne ovat yhdenmuotoisia pienten osiensa kanssa. Puhutaan itsesimilaarisuudesta.

Samaan fraktaaliin voidaan päätyä toistakin tietä [3]. Korvataan jana kolmesta osajanasta muodostuvalla murtoviivalla (kuva 3). Sen osajanat ovat pituudeltaan puolet edellistä janasta. Viivan kokonaispituus kasvaa siten 1,5-kertaiseksi. Korvataan edelleen jokainen osajana vastaavalla yhdenmuotoisella murtoviivalla. Murtoviivan pituus kasvaa rajatta korvaamisen edetessä. Lopuksi päädytään Sierpinskin kolmioon. Tämä auttaa ehkä vahvistamaan sitä käsitystä, että lopputulos ei ole yksiulotteinen viiva, mutta ei myöskään kaksiulotteinen pinta.

Pascalin kolmio
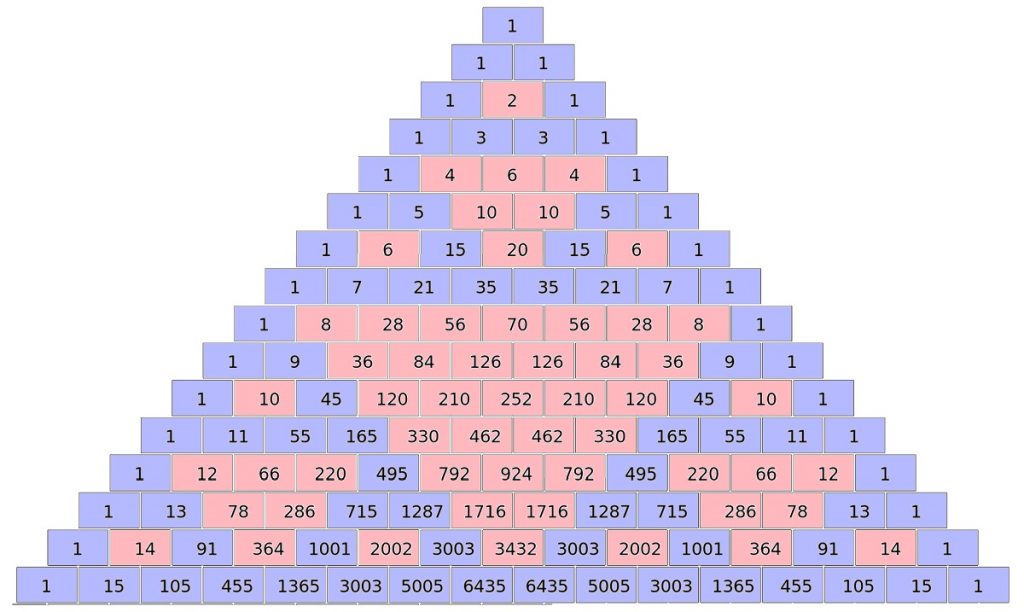
Auki kirjoitetun binomin potenssin termien kertoimet eli binomikertoimet voidaan järjestää kolmionmuotoiseksi taulukoksi eli Pascalin kolmioksi [4]. Jos väritetään parittomien lukujen taustat sinisiksi ja parillisten punaisiksi, niin saadaan aivan samantapainen kuvio kuin alussa värien yhteenlaskun perusteella saatiin (kuva 4). Syykin on ilmeinen. Luvut saadaan nimittäin lasketuiksi myös ilman mitään tietoa polynomeista. Reunoilla on ykkösiä ja muut luvut saadaan laskemalla yhteen kaksi vierekkäistä edellisen rivin lukua. Siis vastaava periaate, jolla värineliöistä muodostuva kolmio rakentui.
Väritetystä Pascalin kolmiosta havaitaan muutakin. Esimerkiksi se, että on joitakin binomin potensseja, joiden kaikki kertoimet ovat parittomia. Ne vastaavat binomin potensseja 0, 1, 3, 7 ja 15. Näistä sääntö on jo nähtävissä. Kaikki kertoimet ovat parittomia [5], kun binomi korotetaan potenssiin, joka on muotoa $2^k-1$, missä $k$ = 0, 1, 2, 3, …
Lähteitä ja lisätietoa:
[1] Lehto, S. Toiminnallista matematiikkaa: Fraktaaliaskartelua osoitteessa https://matematiikkalehtisolmu.fi/2005/3/saara.pdf
[2] Esimerkiksi Ortiz, M. Sierpinski Triangle osoitteessa https://www.geogebra.org/m/gFda256X
[3] Constructing the Sierpinski triangle osoitteessa https://www.oftenpaper.net/sierpinski.htm
[4] Pascal’s Triangle divisible by 2 osoitteessa https://commons.wikimedia.org/wiki/File:Pascal%27s_Triangle_divisible_by_2.svg
[5] Odd Binomial Coefficients? osoitteessa https://math.stackexchange.com/questions/148017/odd-binomial-coefficients
Kuvan 3 murtoviivat on piirretty MSWLogolla, Ohjelmakutsu on esimerkiksi kuva 300 4.
to kuva :jana :toistot
cs rt 90 vs :jana :toistot
end
to vs :jana :toistot
if :toistot = 0 [fd :jana stop]
lt 60 os :jana / 2 :toistot – 1
rt 60 vs :jana / 2 :toistot – 1
rt 60 os :jana / 2 :toistot – 1
lt 60
end
to os :jana :toistot
if :toistot = 0 [fd :jana stop]
rt 60 vs :jana / 2 :toistot – 1
lt 60 os :jana / 2 :toistot – 1
lt 60 vs :jana / 2 :toistot – 1
rt 60
end







