Tylsin luku

Luvuilla on toinen toistaan kiinnostavampia ominaisuuksia sekä numerologiassa että lukuteoriassa. Niistä on kirjoitettu paljon. Onko tylsiä lukuja olemassa? Tai mikä olisi vähiten kiinnostava luku?

Yksittäisiä kiinnostavia lukuja on paljon, tunnetuimpina ehkä π, e, $\sqrt{2}$ tai 10. Voit varmaan helposti keksiä muita, joilla on jokin erityinen ominaisuus tai merkitys, esimerkiksi alkuluvut tai pienten kokonaislukujen potenssit tms. Kaikkien kiinnostavuutta ei ole aina helppo havaita. Tunnettu on tarina luvusta 1729, jonka Ramanujan tiesi olevan pienin luonnollinen luku, joka voidaan esittää kahden kolmannen potenssin summana kahdella eri tavalla.

Luonnollisten lukujen kiinnostavuuden mittana voitaisiin pitää niiden yhteyksiä mihin lukuihin. Yhteyksien runsauden indikaattoriksi sopisi luvun esiintymismäärä luonnollisten lukujen jonojen tietokannassa Online Encyclopedia of Integer Sequences (OEIS [1]). Siellä on nykyisellään yli 370 000 jonoa. Mitä useammassa jonossa (luonnollinen) luku esiintyy, sitä enemmän sillä voidaan katsoa olevan yhteyksiä muihin (luonnollisiin) lukuihin.

Kymmentä tuhatta pienemmistä luonnollisista luvuista OEIS:n sarjoissa jotkut esiintyvät enemmän kuin sata tuhatta kertaa ja vain kolme lukua vain kerran. Nämä viimeksi mainitut ovat kaikki suurempia kuin 8000. – Eikä erottelu jää vain tähän, vaan esiintymistaajuus erottelee luvut kiinnostaviin ja ei-kiinnostaviin (tylsiin). Kaaviossa, jossa kunkin pisteen koordinaatit ovat (luonnollinen luku, sen esiintymistaajuus OEIS:n sarjoissa), voidaan hahmottaa kaksi vyötä, joista toisessa ovat kiinnostavat ja toisessa tylsät luvut. Vöiden väli (Sloanen aukko, kuva [2]) ei ole aivan tyhjä, mutta siinä luvut ovat selvästi harvemmassa kuin kummassakaan vyössä. Tämä merkitsee sitä, että luonnolliset luvut esiintyvät sarjoissa joko usein tai harvoin, mutta välimuotoja on vähän. [3]

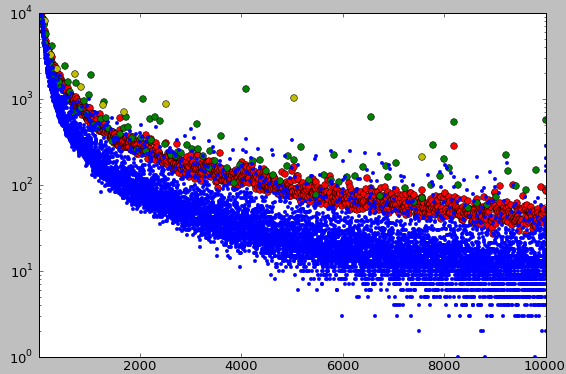
Kiinnostavien lukujen alueessa ovat esimerkiksi lähes kaikki alkuluvut (99,7

Mikä olisi tylsin luku? Onko siis mitään lukua, joka ei olisi kiinnostava jonkin ominaisuutensa takia? Jopa luvulla 10213223 on yksi kiinnostava ominaisuus, vaikka se ei todennäköisesti esiinny OEIS:n jonoissa montakaan kertaa. Se nimittäin kuvaa itsensä rakenteen: yksi nolla, kaksi ykköstä, kolme kakkosta ja kaksi kolmosta. Kysymys ei ole täysin merkityksetön, sillä internet-haku ”most boring number” antaa runsaat 4500 osumaa. Suomeksi samantapaisella haulla ei saa tarkoitettua tulosta, sillä ”luku” voi liittyä sekä lukemiseen että kirjan tekstijaksoon.

Lukua 20067 on tarjottu tylsimmäksi [4]. Kiinnostavan luvun paradoksin [5] mukaan mitään tylsää lukua ei ole olemassa. Tämä perustuu siihen, että jos olisi täysin tylsiä lukuja, niin niiden joukossa olisi pienin, joka siis ei olisi tämän erikoisasemansa vuoksi täysin tylsä. Tällä tavalla joudutaan pudottaman pois jokainen luku yksi kerrallaan täysin tylsien lukujen joukosta. Mitä mieltä sinä olet tylsistä luvuista?

Lähteitä ja lisää luettavaa

[1] OEIS osoitteessa https://oeis.org/?language=finnish

[2] Guglielmetti, Philippe: Sloanen aukko (ranskaksi) osoitteessa https://fr.wikipedia.org/wiki/Fichier:Sloanes_gap.png. WikiMedia Commons, CC BY-SA 4.0.

[3] Bischoff, Manon: The Most Boring Number in the World. Scientific American 3.3.2023. https://www.scientificamerican.com/article/the-most-boring-number-in-the-world-is

[4] LinkedIn-postaus (Matthias Laux) osoitteessa https://www.linkedin.com/posts/matthiaslaux_the-most-boring-number-in-the-world-is-activity-7037815634268688384-j1u3/?originalSubdomain=de

[5] Interesting number paradox osoitteessa https://en.wikipedia.org/wiki/Interesting_number_paradox