Truchet’n laatat
Jean Truchet (1657–1729) liittyi kuusitoistavuotiaana karmeliittaveljeskuntaan. Siinä yhteydessä hän otti nimekseen Sébastien hurskaan äitinsä Sébastienen kunniaksi. Häntä ei kuitenkaan tunneta kirkollisista, vaan teknisistä ansioistaan. Hänen alojaan olivat matematiikka, hydrauliikka ja typografia. Monien keksintöjensä perusteella häntä on kutsuttu mekaniikan neroksi.
Vuonna 1693 hänet valittiin komiteaan, jonka tehtävänä oli laatia kuvaus kaikista Ranskan taiteellisista ja teollisista prosesseista. Siinä työssä saavuttamiensa ansioiden perusteella hänet nimitettiin Ranskan kuninkaallisen tiedeakatemian kunniajäseneksi (honoraire) vuonna 1699.
Merkittävin, vaikka ei ehkä tunnetuin Truchet’n keksinnöistä on tekstin koon mitta eli typografinen piste. Sitä nimitetään Ranskassa vieläkin Truchet’n pisteeksi. Pisteen todellinen koko on vaihdellut jonkin verran ajan mukana, mutta perusidea on edelleen sama. Esimerkiksi tämän Dimensio-lehden leipätekstin pistekoko on 11, kirjaintyyppi Montserrat.
Sama komitea määritteli myös uuden tekstityypin nimeltä Roman du roi. Se on yksi päätteellisistä antiikva-perheen (engl. sherif tai Roman) tekstityypeistä. Tällaisia tekstityyppejä oli määritelty jo renessanssin aikana, mutta uutta oli se, että kirjaimet muodostettiin neliöruudustoon piirretyistä geometrisista muodoista. Roman du roi on ollut muun muassa nykyään yleisesti käytetyn Times New Roman -tekstityypin pohjana.
Kaksivärilaatat
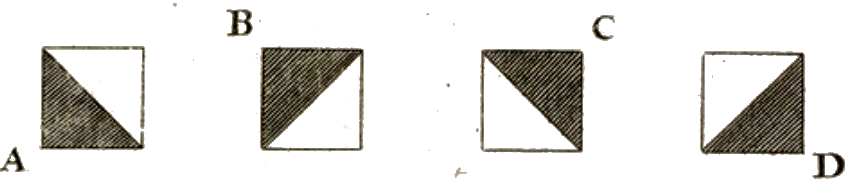
Mahdollisesti juuri Roman du roi -tekstityypin kirjainten määrittely neliöruudukon avulla johti Truchet’n tutkimaan neliöistä koostuvia laatoituksia. Esimerkin hän oli löytänyt Motte S. Lyén linnasta Orleansin läheltä. – Yksinkertaisin Truchet’n laatta on neliö, joka on jaettu lävistäjällä kahteen osaan ja osat on väritetty erivärisiksi. Laatalla on nelinkertainen kiertosymmetria. Jos kiertoja ei sallita, niin on siis olemassa neljä erilaista laattaa (kuva 1).
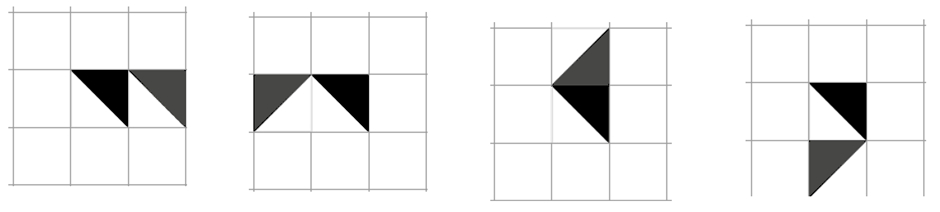
Otetaan kaksi laattaa ja asetetaan ne vierekkäin. Ensimmäisellä laatalla on neljä erilaista mahdollisuutta, samoin toisella. Jos ajatellaan, että toinen laattaa voidaan asettaa kullekin ensimmäisen laatan neljästä sivusta: oikealle, vasemmalle, ylös, alas, niin saadaan 64 erilaista asetelmaa. Näissä on 32 samanlaista paria. Kuvassa 2 on näistä neljä, ensimmäinen laatta tummempi. Mahdollisuuksien määrä kasvaa hyvin nopeasti, kun otetaan mukaan useampia laattoja.
Näistä neljästä laatasta voidaan rakentaa sekä jaksollisia että jaksottomia laatoituksia. Jaksollisissa laatoituksissa on mukana kaksitoista kaikkiaan seitsemästätoista seinäpaperisymmetriaryhmästä. Pois jäävät vain kolmin- ja kuusinkertaiset kiertosymmetriat. Jaksottomista laatoituksista olkoot esimerkkeinä täysin satunnaiseen sijoitteluun perustuvat laatoitukset (kuva 3).

Kuva 3: Täysin satunnaisia tason peittoja kaksivärisillä Truchet’n laatoilla. Kuvalähde: Geogebra-matletti https://www.geogebra.org/m/rdm9sdck.
Truchet julkaisi tutkimustensa tuloksia ensimmäisen kerran Ranskan kuninkaallisen tiedeakatemian julkaisusarjassa Comptes rendus vuonna 1704. Tutkimukset eivät herättäneet suurta huomiota aikanaan, vaikka Dominique Douat jatkoi tutkimuksia julkaisussaan 1722. Vasta Cyril Stanley Smith teki Truchet’n laatat tunnetuksi artikkelissaan The Tiling Patterns of Sebastien Truchet and the Topology of Structural Hierarchy (Leonardo, 20:4, s. 373–385, MIT Press 1987). Artikkeli sisältää englanninkielisen käännöksen Truchet’n alkuperäisestä artikkelista, saatavissa vain luku -muodossa osoitteesta https://www.jstor.org/stable/1578535?read-now=1&seq=3#page_scan_tab_contents.
Muita laattoja
Smithin artikkeli herätti suurta kiinnostusta ja innostusta. Google-haku ”Truchet tiles” antaa 77 000 tulosta. Kirjavuudesta saa jotain käsitystä esimerkiksi Depositphoto-kuvapankin ilmaiskuvien sivulta https://depositphotos.com/fi/vectors/kuusikulmio-laatat-lattia.html.
Geogebran materiaaleissa on vastaavasti sata työtä. Suomeksi Truchet’n laatoista ei näytä kirjoitetun.
Kaksivärilaatan ohella yksinkertaisimpia on laatta, jossa on vain kaksi neljännesympyrän kaarta. Sillä on nelinkertainen kiertosymmetria, mutta kierroista saadaan vain kaksi erilaista (kuva 4, vasen kuvapari). Näistä kahdesta laatasta satunnaisesti kootut tason täytöt koostuvat ympyröistä ja monimutkaisemmista kaarevista viivoista (kuva 4, neljä oikeanpuoleista).

Truchet’n laattoja vastaavalla idealla on luotu sadoittain erilaisia laattoja ja niistä muodostuvia tason peittoja sekä matemaattisista että esteettisistä motiiveista lähtien, esimerkiksi https://questionsindataviz.com/2021/03/03/what-are-truchet-tiles/ ja https://fi.pinterest.com/pin/532621093429037417/. On myös Truchet-peittoja tuottavia generaattoreita: https://dmackinnon1.github.io/truchet/gen.html ja https://truchetpatterns.netlify.app/.







