Tilkkumatematiikkaa

Seuraava hyvin omakohtainen tarina kertoo uuden harrastuksen aloituksesta, mutta tuo myös esille sitä kuinka erilaisissa yhteyksissä matematiikkaa ja mittaamista tarvitaan. Loppuosan esimerkkejä voi soveltaa haluamallaan tavalla myös matematiikan tunneilla. Paperillakin voi tehdä monenlaisia testauksia, ompelukone ei useinkaan ole saavutettavissa matematiikanluokassa. 

Opettajakin tarvitsee kiinnostavia harrastuksia ja niille myös aikaa. Ollessani päätoimisesti töissä yritin jatkuvasti löytää aikaa sellaiselle tekemiselle, josta näkee konkreettisen tuloksen kohtuullisessa ajassa. Käytännössä tämä tarkoitti lähinnä sukkien kutomista. Sukka on käyttötavara ja kohtuullisella vaivalla saatavissa aikaan. Jopa kaksi sukkaa. Omaa luovuutta saa käyttää värien ja mallien kanssa ja laskemaankin pääsee, jotta sukasta tulisi järkevän kokoinen.  Sukkia on syntynytkin vuosien varrella niin paljon, että lähivuosisatoina ei tarvitse ainakaan oman perheen tarpeiksi kutoa lisää.

Ensimmäisessä eläköitymisvaiheessani (pari muutakin tuli myöhemmin), toteutin pitkäaikaisen haaveeni ja ostin ompelukoneen. En ollut muinaisen keskikoulun jälkeen ommellut eikä minulla ollut vähäisintäkään käsitystä edes ompelemisen perusteista.  Suoraan syvään päähän siis.  Apua koneen hankintaan sain onneksi käsityöguru Sari Yrjänäiseltä.

Miksi juuri tilkkutyöt? 

Matematiikasta innostunutta tilkkutyöt ovat aina viehättäneet, joten ilmoittauduin paikallisen kansalaisopiston tilkkukurssille.  Motivoivaa oli havaita, että ryhmän kymmenestä jäsenestä olin ylivoimaisesti nuorin ja mukana oli vain kaksi aloittelijaa. Toinenkin vasta-alkaja oli toiminut matematiikan opettajana. Konkarikurssikaverit sanoivat heti, että haastetta tulee riittämään. Olivat oikeassa.

Tilkkuilussa käytetään nimensä mukaisesti pieniä kangaspaloja ja pyritään välttämään hukkapalojen syntyä. Pelkästään tähän tarvitaan hahmotuskykyä ja laskemista. Halutut palat on leikattava mahdollisimman tarkasti, millimetri on useimmin käytetty yksikkö ja kulmat pitää saada tarkasti halutun kokoisiksi. Tilkkutöissä on paljon käyttöä muullekin kuin suoralle kulmalle. Oma osaamiseni ei ole vielä kovin pitkällä tältä osin, mutta etenee askel askeleelta. 

Paloja voi leikata saksilla, mutta useiden täsmälleen samankokoisten palojen leikkaaminen saksilla on hankalaa. Siitä syystä tilkkutöissä käytetään useimmiten erillistä leikkausalustaa ja pyöröleikkuria, jollaiseksi sopii myös terävä mattoleikkuri. Näiden avulla tarkkuus paranee.

Keskeinen asia tilkkuja ommeltaessa on pitää mielessään saumavara, joka on lähes kaikissa ohjeissa määritelty 0,75 cm levyiseksi. Jos saumavara unohtuu, alkuperäinen suunnitelma menee todennäköisesti metsään. Tuli kokeiltua.  Saumavara tarvitaan jokaiselle sivulle, joka on tarkoitus ommella toiseen palaseen tai taustakankaaseen.

Fibonaccin kaitaleet

Pannulappu on sukkaan verrattava sopivan kokoinen käyttötavara.  Kokeneemmat tekivät ja tekevät isoja tilkkupeitteitä, minä aloitin pannulapulla. Tavoitteeksi asetettiin neliön muotoinen pannulappu, jossa neliön sivu valmiissa tuotteessa olisi esimerkiksi 29 cm. Yhdestä kangaspalasta tekeminen on kohtuullisen selkeä homma. Vaikeusastetta lisää haaste, jossa pinta tehdään kahdesta kankaasta suikaleittain ja suikaleiden leveys noudattaa Fibonaccin lukusarjaa.

Tarvitaan siis kaksi kangasta ja niistä neliön muotoiset palaset 29*29. 

Fibonaccin lukusarjakin on tuttu 1,1,2,3,5,8,13…

Kuinka leveitä suikaleiden pitää olla, jotta ne saadaan ommeltua yhteen siten, että esille jää alkuperäinen tavoiteleveys?  Suikaleiden yhteenlaskettu leveys pitää olla 29 cm, jotta saadaan neliö aikaan. (kuva)

Lasketaanpa lähtien Fibocaccin luvuista:

1+ 1,5 cm = 2,5 cm. Tuo 1,5 cm tulee kummankin puolen saumavaroista 2*0,75 cm. 

1+1,5 = 2,5 cm

2+1,5 cm = 3,5 cm

3+1,5 = 4,5 cm

5+1,5 cm = 6,5 cm 

8+1,5 cm = 9,5 cm

13 + 1,5 cm =14,5 cm  

jne.

Lasketaan sitten suikaleiden leveyksiä yhteen: 2,5 cm+2,5 cm+3,5 cm+4,5 cm +6,5 cm +9,5 cm = 29 cm.

Opettaja oli siis fiksusti säästänyt laskemisen vaivan ja antanut järkevän luvun alkuperäisen neliön sivuksi. Erilaisia muuntamismahdollisuuksia on valtavasti. 

Nyt pannulappu on mahdollista ommella vaihdellen eri kankaasta leikattujen suikaleiden paikkaa siten, että saadaan värikäs kokonaisuus. Jos ensimmäinen kangas on A ja toinen B, ensimmäisessä vaiheessa kankaiden järjestys on ABABAB ja BABABA. Kun suikaleet ommellaan yhteen, saadaan kaksi neliötä. Nämä viipaloidaan uudelleen poikittain taas Fibonaccin lukujen suhteessa ja ommellaan taas yhteen poikittain. Muodostuva taso on hauska. Jos olisi valinnut kankaat fiksummin, tasoon saisi kolmiulotteista vaikutelmaakin, mutta enhän sitä alkuvaiheessa osannut.

 Kuvassa osa ensimmäisestä tuotoksestani, jossa kulmien kohdistus on vielä aika kaukana tavoitteesta.

Neliöt ja kolmioneliöt

Erilaisten kangasneliöiden yhdistäminen toisiinsa on hyvin helppo ja aloittelijallekin sopiva tapa tehdä tilkkupintaa. Sillä oli hyvä aloittaa seuraava projekti – yllätys, yllätys pannulappu. 

Entäpä, jos neliö halutaankin korvata kahdella suorakulmaisella kolmiolla? Miten olisi järkevintä tehdä kahdesta eri kankaasta kolmioita, joista saadaan halutun kokoinen neliö, osaksi laajempaa neliöpintaa tai vaikkapa kokonaan kolmioituna? Ja ne saumavarat mukaan. Nopealiikkeisenä tein monta versiota, joissa neliön sivun pituus oli väärä. Olin tietysti unohtanut saumavarat.

Oletetaan, että tavoitteena on tehdä kankaista kahdesta kolmiosta muodostuva neliö, jonka sivu on esimerkiksi 8 cm. Kolmiot voi halutessaan tehdä yksitellen mitaten ja leikaten tai vaikkapa valmiin sabluunan avulla. 

Helpohko tapa monistaa useita kolmioita pienellä vaivalla on tehdä kolmioneliöitä tilkkuyhdistyksen ohjeen mukaisesti. [1] 

Ohessa menetelmä pähkinänkuoressa.

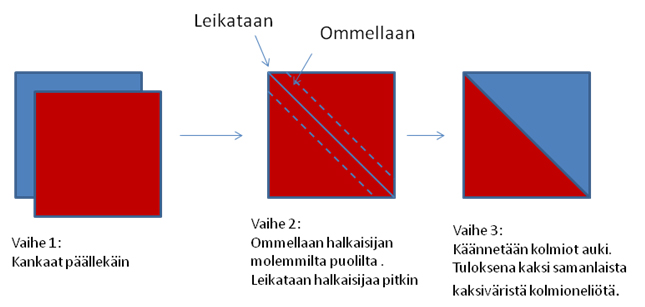
Kysymys: Kuinka suuri neliön sivun pitää olla, että tuloksena syntyvä kahdesta kolmiosta muodostuvan neliön sivu olisi 8 cm?

Pienestä isommaksi

Tilkkutöissä rakennetaan usein pienemmistä blokeista isompia, jolloin tuotoksen pinnan vaihtelut voivat olla hyvin erilaisia. Omat taitoni riittävät hyvin yksinkertaisiin malleihin, mutta niidenkin avulla saadaan jännittäviä kuvioita kuten oheinen yksityiskohta pöytäliinasta kertoo.  Samalla näkyy neliöblokki, josta kaitaliina koostuu.

Ennalta on tärkeää pohtia, minkä kokoisen tuotoksen (kassin, pannulapun, tilkkupeitteen jne) haluaa lopputuloksena ja sen jälkeen laskea tarvittavien blokkien määrää.  Kokemus on myös karvaasti opettanut, että kankaan riittävyyskin kannattaa arvioida ja tarkistaa ennalta. Vaikeustasoa voi nostaa itselleen haluamalla vaikkapa vetoketjun kassiin tai pussukkaan. Vetoketjun voi muuten ommella ainakin seitsemän kertaa väärinpäin. Hermot ovat joskus olleet koetuksella, mutta pienetkin onnistumiset palkitsevat sitten monin verroin. 

Konkreettinen ompelutyö onnistuu kyllä aloittelijaltakin, jos matemaattinen puoli on laskettu oikein ja mittaaminen suoritettu tarkasti. Yhdenkin millimetrin heitto kertautuu nopeasti. 

Tilkutus on harrastus, joka lähtee lentoon hyvin nopeasti, koska jokainen uusi työ tarjoaa mukavasti ja  välillä hiukan liikaakin haasteita. Kurssilla jatkan edelleen ja opin kaiken aikaa lisää. Pelkästään kokeneempien tuotoksia katsellessa into kasvaa entisestään. Yhdessä opitaan.

Kuvat: Kaisa Vähähyyppä.

Lähteet

[1] Tilkkuyhdistys Finn Quilt ry: Kolmio-neliöt helposti – Ja kaksi lisäideaa. https://finnquilt.fi/ompele-kolmio-nelioblokki/