Suunnikkaan pinta-ala japanilaisittain

Tässä artikkelissa tarkastelen japanilaisen matematiikan opetuksen piirteitä sekä seuraamaani japanilaista matematiikan tuntia. Seuraamani tunnin aiheena oli suunnikkaan pinta-alan määrittäminen. Sen sijaan, että asia olisi käsitelty opettajajohtoisesti, oppilaat itse kehittivät useita erilaisia menetelmiä alan määrittämiseksi. Tunnin lopussa oppilaiden ratkaisumenetelmistä käytiin hedelmällinen keskustelu. Tunti havainnollistaa avoimen lähestymistavan ja japanilaisen matematiikan opetuksen hyviä puolia.

Japanilainen matematiikan opetus

Sekä suomalaista että japanilaista matematiikan opetusta on pidetty korkeatasoisena ja maat ovat menestyneet kansainvälisissä arviointitutkimuksissa (esim. OECD, 2010). Kuitenkin suomalainen ja japanilainen matematiikan opetus poikkeavat huomattavasti toisistaan. Suomessa tyypillisellä matematiikan tunnilla opettaja ensin käsittelee uuden asian, jota sitten harjoitellaan käyttämään oppikirjan tehtävissä (Savola, 2008; Tourunen, 2011). Shimizun (1999) mukaan tyypillisen japanilaisen matematiikan tunnin rakenne on seuraava:

1. Ongelman esittely
2. Oppilaiden yksilöllinen ongelman ratkaisu
3. Koko luokan keskustelua ratkaisumenetelmistä
4. Opettajan yhteenveto

Tunnin onnistumisen kannalta ratkaisevana Japanissa pidetään oppilaiden ratkaisumenetelmistä keskustelemista, josta Japanissa käytetään termiä ”neriage” (Shimizu, 1999; Takahashi, 2008). Ratkaisumenetelmistä keskustelemisen ideana on käsitellä opettajan valikoimien ratkaisujen yhtäläisyyksiä ja eroja sekä etuja ja haittoja ja näin oppia tavoitteena oleva asia. ”Neriage” tarkoittaakin oppilaiden ideoiden viimeistelyä ja yhteisen integroidun matemaattisen idean kehittämistä opettajan johtamassa koko luokan keskustelussa (Shimizu, 1999). Sekä Suomessa että Japanissa pyritään siihen, että oppilaat ratkaisevat tehtäviä tunnilla. Japanissa oppilaat kuitenkin ratkaisevat tehtäviä ennen tunnin lopussa tapahtuvaa uuden asian opettamista, kun taas Suomessa oppilaat useimmiten tekevät tehtäviä vasta uuden asian opettamisen jälkeen (Hino, 2006; Tourunen, 2011).

Matematiikan opiskelemisen kulttuuria voidaan kuvata normeilla, joilla tarkoitetaan opettajan ja oppilaiden käyttäytymisodotuksia eli ryhmän toimintaa kuvaavia säännönmukaisuuksia. Sekiguchi (2006) havaitsi seuraavien normien kuvaavan japanilaisten matematiikan ryhmien toimintaa:

• Ryhmän jäsenten tulee kehittää useita matemaattisesti erilaisia ideoita.
• Ryhmän jäsenten tulee pyrkiä kohti mahdollisimman tehokkaita ratkaisumenetelmiä.
• Ryhmän jäsenten tulee tarkastella mitä matemaattisesti tärkeitä ideoita on löydettävissä virheellisistä ratkaisuyrityksistä.
• Matemaattisessa selityksessä ei voida kirjoittaa mitään, mitä ei ole näytetty toteen.
• Ryhmän jäsenten tulee reflektoida matemaattisen toiminnan tarkoitusta.

Japanilaisessa matematiikan opetuksessa ongelmanratkaisun ja matemaattisen ajattelun painottamisella on pitkät perinteet (Iwasaki & Ueda, 1999).

Avoin lähestymistapa

Toinen japanilaista matematiikkaa kuvaava piirre on avoin lähestymistapa (Nohda, 2000; Ueda, 2000; Pehkonen, 2011). Avoimessa lähestymistavassa oppiminen alkaa avoimista ongelmista, joissa lähtötilanne, lopputilanne tai prosessi on avoin. Jos lähtötilanne on avoin, ratkaisijan pitää itse osallistua ongelman muodostamiseen tekemällä valintoja siitä, mitä asiaa ongelmasta tarkastelee. Jos taas lopputilanne on avoin, ongelmaan on useita oikeita ratkaisuja. Myös prosessi voi olla avoin, jolloin tehtävän voi ratkaista usealla eri tavalla. Avoimen lähestymistavan on tarkoitus kehittää matemaattista ajattelua kaavamaisen suorittamisen sijasta (Nohda, 2000; Ueda, 2000). Uedan (2000) mukaan avoimella lähestymistavalla on seuraavia etuja:

• Oppilaat tuntevat osallistuvansa matematiikan tunnilla ja alkavat keskustella matematiikasta.
• Oppilailla on paljon mahdollisuuksia integroida oppimiaan tietoja ja taitoja sekä käyttää niitä ymmärtäen.
• Kaikentasoisilla oppilailla on mahdollisuus saada oikea vastaus.
• Oppilaat ovat motivoituneita omien ideoidensa selittämiseen ja perustelemiseen.
• Oppilaat saavat kokea löytäneensä itse jotain matematiikasta ja iloita ajatustensa jakamisesta.

Avoimella lähestymistavalla yhdistettynä japanilaisen matematiikan tunnin rakenteeseen on myös paljon yhteistä tutkivaksi matematiikaksi kutsumani opetusmenetelmän kanssa (Hähkiöniemi, 2011).

Japanilainen 5. luokan tunti Suunnikkaan pinta-alasta

Olin syksyllä 2010 vierailulla Hiroshiman yliopistossa professori Atsumi Uedan kutsumana. Osana vierailua seurasimme yhden 45 minuutin viidennen luokan tunnin tavallisessa koulussa. Tässä esittämäni havainnot tuosta oppitunnista perustuvat tekemiini muistiinpanoihin. Tunnilla oli mukana tulkki, joka käänsi tärkeimmät tunnin osat englanniksi tunnin aikana. Lisäksi minulla oli englanniksi käännetty tuntisuunnitelma.

Tuntisuunnitelma

Tunnin aiheena oli suunnikkaan pinta-alan määrittäminen. Oppilaat olivat aikaisemmin opiskelleet suorakulmion alan määrittämisen, mutta suunnikaan pinta-alaa käsiteltiin tällä tunnilla ensimmäisen kerran. Opettajalla oli paljon kokemusta, ja hän oli toteuttanut tämän tunnin useaan kertaan. Hän oli laatinut tuntia varten kuusisivuisen tuntisuunnitelman. Tuntisuunnitelman pääosa oli taulukko, jossa oli esitetty tunnin oppimisaktiviteetit, hypoteeseja oppilaiden mahdollisesta toiminnasta sekä opettajan mahdollisia tapoja tukea oppilaita (Taulukko 1). Samankaltainen tuntisuunnitelmataulukko on Japanissa yleinen (Shimizu, 1999).

Taulukko 1. Tuntisuunnitelma.

Oppimisaktiviteetit (kysymykset)	Hypoteesit oppilaiden mahdollisesta toiminnasta tai reaktioista	Opettajan mahdollinen tuki
Esimerkiksi tunnin rakenteen opettaja oli hahmottanut seuraavasti: 1. Ongelman ymmärtäminen 2. Yksilöllinen oppiminen 3. Kollektiivinen oppiminen 4. Reflektointi	Opettaja oli esimerkiksi esittänyt monta erilaista tapaa määrittää suunnikkaan ala.	Opettaja oli esimerkiksi kirjoittanut, että oppilaat saavat selittää ideansa ja tarkastella yhtäläisyyksiä muiden oppilaiden ideoihin.

Ongelman alustus

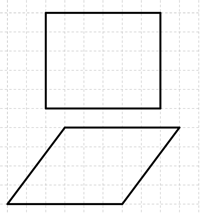
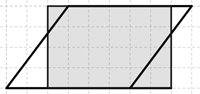
Tunnin alussa opettaja esitti taululla suorakulmion ja suunnikkaan, joiden sivujen pituudet olivat samat (Kuva 1). Opettaja kyseli oppilailta, mitä yhteistä ja mitä eroa nelikulmioilla on. Näin opettaja varmisti, että oppilaat kiinnittävät huomiota siihen, että nelikulmioiden piirit ovat yhtä suuret. Piirien yhtäsuuruutta havainnollistaakseen opettaja oli rakentanut pilleistä ja narusta suunnikkaan, jonka kulmia pystyi muuttamaan, mutta sivujen pituuksia ei (Kuva 8). Keskustelun aluksi oppilaat olivat sitä mieltä, että suorakulmion ja suunnikkaan alat ovat yhtä suuret. Lisäksi oppilaat laskivat suorakulmion alaksi $5\cdot6=30$. Mittayksikön huomioiden he saivat vastaukseksi 30 cm². Näin tunnin aiheen kannalta tärkeä ennakkotieto eli suorakulmion alan laskeminen tuli myös kerratuksi.

Kun oppilaat olivat sitä mieltä, että suorakulmion ja suunnikkaan pinta-alat ovat yhtä suuret, opettaja ei ottanut kantaa siihen, ovatko oppilaat oikeassa. Sen sijaan opettaja kysyi oppilailta, miksi alat ovat yhtä suuret. Oppilaat äänestivät innokkaina asiasta ja vähitellen oppilaat alkoivat vaihtaa mielipidettään. Tässä vaiheessa opettaja selvitti oppilaille, että nyt on tarkoitus pohtia, miten suunnikkaan pinta-ala voidaan laskea. Näin opettaja oli alustanut ongelman, varmistanut oppilaiden ymmärtävän ongelman, kerrannut ratkaisussa tarvittavat tiedot, korostanut tunnin tavoitetta ja motivoinut oppilaita ongelman ratkaisemiseen. Tämän jälkeen opettaja jakoi oppilaille kuvassa 1 esitetyn monisteen, jossa kysyttiin heidän ideaansa suunnikkaan alan laskemiseksi. Tässä vaiheessa aikaa oli kulunut 15 minuuttia.

Yksilöllistä ongelmanratkaisua

Opettajan jaettua monisteet oppilaat alkoivat yksinään hiljaa työskennellen ratkaista ongelmaa. Opettaja ajasti munakelloon 7 minuuttia aikaa yksilölliseen työskentelyyn. Opettaja kierteli luokassa seuraamassa oppilaiden työskentelyä. Kun oppilas oli keksinyt yhden tavan laskea suunnikkaan ala, hän sai hakea opettajan pöydältä uuden monisteen ja alkaa keksiä toista, erilaista ratkaisutapaa. Monet oppilaat ehtivätkin hakea toisen monisteen. Esitän esimerkkejä oppilaiden ratkaisumenetelmistä tuonnempana.

Ratkaisuideoiden selittäminen vierustoverille

Munakello ilmoitti yksilöllisen työskentelyn päättyneen 7 minuutin kuluttua. Opettaja pyysi oppilaita selittämään ratkaisuideansa vierustoverilleen. Tähän käytettiin aikaa 5 minuuttia.

Koko luokan keskustelua ratkaisumenetelmistä

Loppuosa tunnista (18 min) käytettiin opettajan johdolla käytävään koko luokan keskusteluun. Opettaja pyysi aluksi viittä oppilasta esittämään ratkaisunsa. Opettaja oli ilmeisesti valinnut nämä oppilaat jo edellisissä vaiheissa, koska oppilaiden ratkaisut olivat erilaisia. Oppilaat tulivat yksitellen luokan eteen näyttämään ja selittämään menetelmänsä suunnikkaan pinta-alan laskemiseksi. Opettaja oli varannut valmiiksi pahvista leikattuja oikeankokoisia suunnikkaita, joihin oppilaat saattoivat piirtää tai joita he voivat leikata. Ratkaisumenetelmät kiinnitettiin taululle vierekkäin, ja jokaisen menetelmän yläpuolelle opettaja kiinnitti oppilaan nimikyltin. Oppilaiden nimiä käyttämällä opettaja vahvisti käsitystä siitä, että tunnilla rakennettava matematiikka on oppilaiden omaa matematiikkaa. Seuraavassa ratkaisut esitetään siinä järjestyksessä kuin oppilaat ne esittivät.

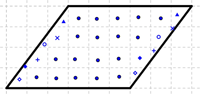
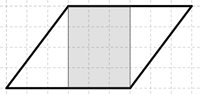
Oppilas A esitti ratkaisuksi kokonaisten ruutujen laskemisen. Hän aloitti laskemalla kaikki kokonaiset ruudut, joita oli 18. Oppilas havainnollisti näitä kokonaisia ruutuja pienillä ympyräsymboleilla (Kuva 2). Tämän jälkeen oppilas yhdisti vaillinaisista ruuduista pareittain kokonaisia. Aina yhtä paria, jotka muodostivat kokonaisen ruudun, hän merkitsi tietyllä symbolilla (Kuva 2). Yhdistelemällä hän sai 6 kokonaista ruutua. Yhteensä hän sai siis pinta-alaksi 24 cm². Tässä menetelmässä korostuu hyvin pinta-alan perusidea eli se, että pinta-ala neliösenttimetreinä tarkoittaa, kuinka montaa neliösenttimetrinkokoista ruutua alue vastaa.

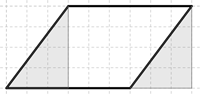
Oppilaan B ratkaisumenetelmänä oli leikata suunnikkaasta kolmio ja liittää se toiselle puolelle suunnikasta niin, että muodostui suorakulmio (ks. Kuva 3). Suorakulmion alaksi oppilas laski $4\cdot6=24$ eli vastaukseksi hän sai 24 cm². Tämä ratkaisu havainnollistaa, että pinta-ala säilyy samana, vaikka alue jaetaan osiin ja osia siirrellään. Muuttamalla alue suorakulmioksi on sen sisältämien neliösenttimetrien (ruutujen) määrä helppo laskea kertolaskulla.

Oppilas C selitti ratkaisuaan ensin suullisesti ja piirtämällä. Hänen ideansa oli tehdä esitetyt kaksi leikkausta (Kuva 4) suunnikkaan eri puolille. Hänen selittäessään ratkaisuaan luokkaan laskeutui odottava hiljaisuus.

Luokka seurasi jännittyneenä, kun oppilas C opettajan avustuksella konkreettisesti leikkasi kaksi syntynyttä kolmiota irti ja siirsi ne niin, että muodostui suorakulmio (Kuva 5). Samalla hetkellä luokasta kuului kunnioittava huokaus: ”Oo!” Tämä ratkaisu havainnollistaa hyvin, että luovatkin ratkaisut ovat mahdollisia, kun oppilaat saavat itse osallistua matematiikan tekemiseen.

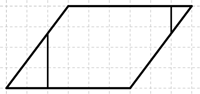
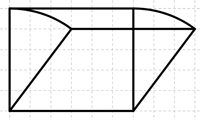
Oppilaan D ratkaisu oli jakaa suunnikas suorakulmioksi ja kahdeksi kolmioksi (Kuva 6). Suorakulmion alaksi hän laski $4\cdot3=12$ ja kolmioiden yhteenlasketuksi alaksi $4\cdot3=12$. Siten hän sai vastaukseksi 24 cm².

Oppilas E näytti oman ratkaisunsa dokumenttikameralla, koska hän oli tehnyt merkintöjä paperiin. Hänen ideansa oli, että suunnikkaan ala on yhtä suuri kuin suorakulmion, jonka sivut ovat samanmittaiset. Hän oli havainnollistanut ratkaisuaan piirtämällä ympyrän kaaret (Kuva 7). Siten hänen ratkaisunsa suunnikkaan alaksi oli $5\cdot6=30$.

Oppilaan E ratkaisu on arvokas, koska se ympyrää hyödyntäen tuo loistavasti esille, että suunnikkaita, joilla on sama piiri, on monta. Lisäksi sen avulla saadaan vielä käsiteltyä yleinen virhekäsitys, että suunnikkaan ala on sivujen tulo. Luultavasti opettaja oli juuri tästä syystä valinnut tämän oppilaan esittämään ratkaisunsa. Esityksestä syntyikin mielenkiintoinen keskustelu. Opettaja kysyi, mitä mieltä muut oppilaat ovat tästä ideasta, jolloin useat oppilaat vastustivat sitä. Opettaja halusi kuitenkin selityksen, miksei suunnikkaan ja suorakulmion ala ole yhtä suuri. Tällöin eräs oppilas tuli luokan eteen ja näytti pilleistä ja narusta rakennetun havainnollistuksen avulla, ettei ala voi pysyä samana. Tämä näkyi selvästi, kun oppilas muutti suunnikkaan kulman hyvin pieneksi (Kuva 8). Tämä tilanne näyttää, kuinka hedelmällisiä oppilaiden ns. virheelliset ratkaisut voivat olla. Tilanne paitsi ehkäisi virhekäsityksen syntymistä, myös opetti matemaattista ajattelua, tarkemmin sanottuna väitteiden osoittamista epätosiksi. Tunnin jälkeen opettaja kertoi, ettei oppilaalle E luultavasti jäänyt negatiivista mielikuvaa tilanteesta, sillä hän on luonut luokkaan ilmapiirin, jossa kaikkia ideoita arvostetaan. Hän kertoi myös totuttaneensa oppilaansa siihen, että tärkeä ei ole vastaus vaan ajatteluprosessi. Oppilas E oli selvästi ajatellut asiaa, ja hänen panoksensa luokan matematiikan oppimiseen oli merkittävä.

Edellä esitettyjä oppilaiden ratkaisuja käsitellessään opettaja kyseli oppilailta, millaisia yhteisiä piirteitä oppilaiden A–E ratkaisuissa on. Tässä yhteydessä havaittiin muun muassa, että useassa ratkaisussa suunnikas muutettiin suorakulmioksi. Oppilaat myös kehuivat oppilaan A ideaa hyväksi, mutta oikeiden parien yhdistämistä kokonaisten ruutujen muodostamiseksi pidettiin vaikeana. Näin tuli vielä varmistetuksi, että oppilaat arvostavat suunnikkaan muuttamista suorakulmioksi. Opettaja totesi vielä tunnin lopuksi, että ensi kerralla käsitellään, miten suunnikkaan ala voidaan laskea ilman leikkaamista.

Pohdinta

Tunnin rakenne oli sellainen, miksi Shimizu (1999) kuvaa tyypillisen matematiikan tunnin. Aluksi opettaja alusti ongelman varmistaen kaikkien ymmärtävän sen ja herätti oppilaiden motivaation ongelman ratkaisuun. Seuraavassa vaiheessa oppilaat ratkaisivat itsenäisesti ongelman. Oppilaiden välistä vuorovaikutusta hyödynnettiin, kun he yksilöllisen ongelmanratkaisun jälkeen selittivät ideansa vierustoverilleen. Lopuksi oppilaat selittivät ratkaisumenetelmiään ja niistä keskusteltiin opettajan johdolla. Tämä kokoavan vaihe oli tärkeä, sillä ilman sitä oppilaiden tutkimukset olisivat jääneet irrallisiksi. Tunnin rakenne on samanlainen kuin tutkivan matematiikan tunnin rakenne: alustus-, tutkimus- ja koontivaihe (Hähkiöniemi, 2011). Tutkivassa matematiikassa oppilaat työskentelevät kuitenkin useimmiten pareittain tai pienissä ryhmissä.

Tarkastellulla tunnilla sovellettiin myös avointa lähestymistapaa. Tässä tapauksessa ongelma itsessään (tietyn suunnikkaan alan määrittäminen) oli varsin tavanomainen. Mutta se oli oppilaille todellinen ongelma, koska suunnikkaan pinta-alaa ei ollut aiemmin käsitelty. Ongelman avoimuus riippui selvästi kontekstista. Opettaja rohkaisi oppilaita keksimään useita erilaisia ratkaisutapoja, mikä kertoo siitä, että ratkaisuprosessi oli avoin (Nohda, 2000). Oppilaiden luovat erilaiset ratkaisutavat saivat aikaan mielenkiintoisen ja kehittävän keskustelun. Tämä tunti havainnollisti käytännössä Uedan (2000) esittämiä avoimen lähestymistavan etuja.

Jos opettaja ensin käsittelisi suunnikkaan alan kaavan ja sitten oppilaat käyttäisivät kaavaa tehtävissä, korostuisi mekaaninen laskeminen. Näin vahvistettaisiin kuvaa matematiikasta epäluovana sääntöjen seuraamisena. Sen sijaan tarkastellulla japanilaisella tunnilla oppilaat saivat mahdollisuuden itse kehittää menetelmän suunnikkaan alan laskemiseksi. Näin korostettiin matematiikkaa nimenomaan luovana ajatteluna, ja että matematiikassa muodostetaan sääntöjä eikä vain käytetä niitä mekaanisesti.

Lähteet

Hino, K. (2006). The role of seatwork in three Japanese classrooms. Teoksessa D. Clarke, C. Keitel & Y. Shimizu (Toim.), Mathematics classrooms in twelve countries: The insider’s perspective (s. 59-73). Rotterdam, Alankomaat: Sense Publishers.

Hähkiöniemi, M. (Toim.) (2011). GeoGebra-avusteinen tutkiva matematiikka opetusharjoittelussa: tutkimuksia opettajan ja oppilaiden toiminnasta. Jyväskylän yliopisto. Opettajankoulutuslaitos. http://urn.fi/URN:ISBN:978-951-39-4623-4.

Iwasaki, H. & Ueda, A. (1999). Development of mathematics education in Japan from Meiji era to present time: focusing on the change of realism and academism. International Journal of Curriculum Development and Practice, 1, 103–112.

Nohda, N. (2000). Teaching by open-approach method in Japanese mathematics classroom. Teoksessa T. Nakahara & M. Koyama (Toim.), Proceedings of the 24th conference of the international group for the psychology of mathematics education (Vol. 1, s. 39–53). Hiroshima, Japani: PME.

OECD (2010). PISA 2009 Results: What Students Know and Can Do – Student Performance in Reading, Mathematics and Science (Volume I). http://dx.doi.org/10.1787/9789264091450-en.

Pehkonen, E. (2011). Luovuus matematiikassa – Osa 1. eDimensio 2011. http://www.maol.fi/julkaisut/edimensio/dimensiossa-julkaistua/ (viittattu 1.3.2012).

Savola, L. (2008). Video-based analysis of mathematics classroom practice: Examples from Finland and Iceland.

Julkaisematon väitöskirja. The Graduate School of Arts and Sciences, Columbia University.

Sekiguchi, Y. (2006). Mathematical norms in Japanese mathematics lessons. Teoksessa D. Clarke, C. Keitel & Y. Shimizu (Toim.), Mathematics classrooms in twelve countries: The insider’s perspective (s. 289-306). Rotterdam, Alankomaat: Sense Publishers.

Shimizu, Y. (1999). Aspects of mathematics teacher education in Japan: Focusing on teachers’ roles. Journal of Mathematics Teacher Education, 2, 107-116.

Takahashi, A. (2008). Beyond show and tell: Neriage for teaching through problem-solving – Ideas from Japanese problem-solving approaches for teaching mathematics. Topic Study Group 19: Research and Development in Problem Solving in Mathematics Education. ICME11 – 11th International Congress on Mathematical Education, Meksiko, 2008. http://tsg.icme11.org/document/get/827.

Tourunen, M. (2011). Matematiikan opetus Suomessa ja Japanissa. Pro gradu -tutkielma. Matematiikan ja tilastotieteen laitos. Jyväskylän yliopisto.

Ueda, A. (2000). Explanation of the ‘open-ended approach’ in mathematics class. Teoksessa M. Miheso, C.G. Kanja & T. Baba (Toim.), The Open Ended Approach in Mathematics Education: A First Step Towards Classroom Practice in a Kenyan Setting (s. 3–15). SMASSE Project, Nairobi, Kenia.

Kirjoitus julkaistu aiemmin: Dimensio 2/2012