Sanoista ja etäisyyksistä
Luultavasti kukaan matematiikkaa harrastava ei ole välttynyt keskustelulta matematiikan valtakunnallisen kokeen kuudennen luokan tehtävästä. Tehtävä oli luokiteltu olemaan pohtimista ja päättelyä vaativa, ja se oli seuraavanlainen:
Tehtävä. Alla olevassa tienviitassa on kesäolympialaisten viimeisimpiä isäntäkaupunkeja. Päättele puuttuva etäisyys seuraavaan isäntäkaupunkiin Tokioon.
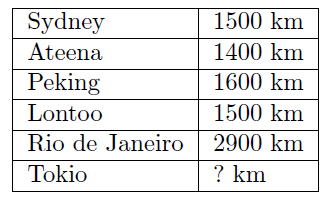
Kyseinen tehtävä oli ajateltu ratkaistavaksi niin, että asetetaan kirjaimille arvot: vokaalit vastaavat lukua $200$ ja konsonantit lukua $300$, jolloin sanasta Tokio tulee $2\cdot 300+3\cdot 200=1200$.
Tämä ei ole aivan ongelmatonta. Minun näkökulmastani tämä havainto on melko keinotekoinen. Lisäksi aakkosten jako vokaaleihin ja konsonantteihin ei ole ainoa mahdollinen tapa jakaa kirjaimet. Eri jakotavoilla saa erilaisia yhtälöryhmiä, joita voi lähteä ratkomaan. Toinen asia on se, että kun tehtävänannossa on mainittu kilometrit, niin se vie ajatuksia fyysisiä etäisyyksiä kohti, jolloin sanan rakenteen analysointi jää luonnollisesti sivuun.
Tämän valituksen jälkeen on todettava, että tällä tehtävällä on myös valtavasti mahdollisuuksia, joita voi vaikka opetuksessa hyödyntää myöhemmin.
Ratkaisu ei aina ole yksikäsitteinen
Aloitetaan toteamalla, että olisin ollut paljon onnellisempi, jos tehtävänanto olisikin ollut tällainen:
Tehtävä. Alla olevassa taulukossa on kesäolympialaisten viimeisimpien isäntäkaupunkien nimiä muutettu luvuiksi jollakin tavalla. Päättele jokin sääntö millä tämä on voitu tehdä, kerro tämä sääntö ja määritä sääntöäsi käyttäen seuraavaa isäntäkaupunkia Tokiota vastaava luku.
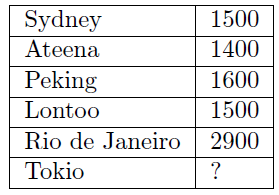
Tällainen tehtävänanto olisi pitänyt yhä sisällään pohtimista ja päättelyä, mutta se olisi minusta ollut paljon reilumpi. Ennen kaikkea siinä olisi tullut ilmi, että ratkaisuja on useita mahdollisia. Tärkeintä ei tällaisessa tehtävässä voi olla lukuarvo, vaan se periaate, jolla se on saatu.
Viesti olisi myös ollut selkeä: matematiikan tehtäviä voi lähestyä usealla eri tavalla. Tyypillisesti tehtävässä on useita eri tapoja ratkaista tehtävä, mutta yksikäsitteinen vastaus. Toisinaan taas dataa on niin vähän saatavilla, että edes vastaus ei ole yksikäsitteinen.
Tyyppiesimerkki tällaisesta tehtävästä, jossa dataa on liian vähän on esimerkiksi tavallinen lukujonotehtävä, joka voisi olla vaikka seuraavanlainen:
Tehtävä. Määritä lukujonon seuraava jäsen, kun lukujonon $(a_n)_{n=1}^{\infty}$ ensimmäiset jäsenet ovat
$1,2,3,6,\dots$
Tähän on erilaisia ilmeisiä ratkaisuja: Mahdollisesti kyseessä on lukujono, jossa seuraava jäsen jäsenestä $a_3$ alkaen on aina kaikkien edellisten jäsenten summa. Tällöin seuraava jäsen olisi siis $12$. Mahdollisesti kyseessä onkin lukujono, jossa kolmannesta jäsenestä lähtien lukujonon jäsen saadaan laskemalla $a_n=a_{n-1}+a_{n-2}+(n-3)$, jolloin seuraava jäsen olisi $a_5=a_4+a_3+(5-3)=6+3+2=11$. Yksi mahdollisuus olisi myös se, että parillisille indekseille pätisi $a_{2n}=2a_{2n-1}$ ja parittomille $a_{2n+1}=a_{2n}+1$ tai vaikka $a_{2n+1}=2a_n-1$. Voisin myös sovittaa vaikkapa kolmannen asteen polynomin $P(x)$ pisteisiin niin, että $P(0)=1$, $P(1)=2$, jne. Vaihtoehtoja on äärettömästi ja niiden rajaaminen vaatisi tarkemmat ehdot kuin mitä pelkkä lukujonon alku antaa.
Toinen ääripää on tehtävä, jossa dataa on auttamatta liikaa, eli kyseessä voisi olla esimerkiksi tällainen yhtälöryhmä:
$\begin{cases}2x+3y & = 5\\ x+y& = 2 \\ 2x+y & = 4.\end{cases}$
Nopeasti näkee, että kahden ensimmäisen yhtälön toteuttavat arvot $x=y=1$, kun taas kaksi jälkimmäistä toteutuvat, kun $x=2$ ja $y=0$. Tyypillisesti tämä tarkoittaisi sitä, että ratkaisuja ei ole. Sen sijaan, jos kyseessä olisikin mittausdata, jossa olisi voinut tulla mittausvirheitä, olisi mielekästä yrittää sovittaa dataan jonkinlainen virheen minimoiva ratkaisu. Siinä tapauksessa luultavasti yhtälöryhmä ei tosin näyttäisi ihan näin siistiltä, mutta ei anneta sen häiritä, sillä ideaa se ei muuttaisi.
Liian usein tuijotetaan yksittäistä ratkaisutapaa tai vain yhtä ratkaisua. Matematiikka ei ole sitä. Matematiikka on pohdintaa. Sujuva tehtävien ratkaiseminen yleensä vaatii fiksun ratkaisutavan löytämistä. Joskus taas ratkaisua ei vain ole tai se ei ole yksikäsitteinen. Tämän keskustelun käymiseen tämä tehtävä toisi loistavan lähtökohdan.
Sanat ja etäisyydet voi yhdistää
Toinen tehtävän tuoma hyvä näkökulma on se, että usein on hyödyllistä yhdistää käsitteet tai menetelmät, jotka eivät lähtökohtaisesti liity lainkaan yhteen. Ei näitä tietenkään ihan miten tahansa yhdistellä, mutta monet tutkimusta eteenpäin vievät oivallukset ovat yhdistäneet keskenään yllättävän menetelmän johonkin vanhaan ongelmaan. Fermat’n suuren lauseen todistus vaati elliptisten käyrien, modulimuotojen ja Diofanteen yhtälöiden yhdistelyä. Nelivärilauseen todistus vuonna 1976 sisälsi sekä puhdasta teoriaa että tietokoneen toteuttamia osia.
Yllättävien asioiden yhdistäminen ei siis ole huono asia. Lisäksi sanojen ja etäisyyksien välillä on yhteys, mutta etäisyyksiä sanojen välillä ei tyypillisesti mitata kilometrein.
Jos sanat ajatellaan yksinkertaisina koodisanoina, eli muutetaan ne nolliksi ja ykkösiksi, jolloin niitä voi käsitellä sopivan vektoriavaruuden alkioina, niin kahden sanan, eli kahden koodivektorin Hammingin etäisyys on niiden koordinaattipisteiden lukumäärä, joissa ne eroavat toisistaan. Esimerkiksi siis vektorien $(0,0,1,1,0)$ ja $(1,0,1,0,0)$ Hammingin etäisyys on $2$, sillä ne eroavat toisistaan ensimmäisen ja toiseksi viimeisen koordinaatin kohdalta. Hammingin paino on vektorin etäisyys avaruutensa nollavektorista, eli sen ykkösten lukumäärä. Esimerkiksi siis vektorin $(0,0,1,1,0)$ Hammingin paino on kaksi.
Tehtävänannon ratkaisu vokaaleilla ja konsonanteilla voitaisiin siis muotoilla näinkin: Muutetaan $n$-merkkinen sana avaruuden $\{0,1\}^n$ sanaksi asettamalla jokainen vokaali nollaksi ja jokainen konsonantti ykköseksi. Tällöin sanaa vastaava etäisyys saadaan laskemalla sanan Hammingin paino, kertomalla se sadalla ja lisäämällä siihen $200n$. Esimerkiksi siis Tokio muutettuna vektoriksi olisi $(1,0,1,0,0)$, jolloin Hammingin paino on $2$, joka kertomalla sadalla saadaan $200$, ja kun $n=5$, niin $200+5\cdot 200=1200$.
Vaikka Hammingin etäisyys onkin varsin kaukana peruskoulun opetussuunnitelmasta, on yleissivistyksen kannalta hyvä tietää, että tietokoneet operoivat nollilla ja ykkösillä ja että näiden nollien ja ykkösten avulla voidaan muodostaa kaikki mahdolliset viestit mitä tietokoneella lähetetään, luvut voidaan muuttaa nolliksi ja ykkösiksi ja jopa tietokoneiden komennot ovat lopulta vain nollia ja ykkösiä. Näillä nollilla ja ykkösillä voidaan tehdä monenlaista matematiikkaa, sekä laskea binääriluvuilla että käsitellä niitä erilaisina vektoreina, ja niillä todella on etäisyys, joka sekin voidaan määritellä eri tavoin riippuen esimerkiksi siitä käsitelläänkö binäärilukuja vai vektoreita.
Matematiikassa harvoin on vain yhtä mahdollista tapaa lähestyä ongelmaa. Tämän viestin viemiseen tätä tehtävää voisi hyvin käyttää.







