Perushahmotusta neljännen ulottuvuuden mieltämiseen, osa3 – Kolmannesta ulottuvuudesta toiseen
Kolmiulotteisesta kappaleesta voidaan piirtää kaksiulotteinen kuva. Matemaattisesti kyseessä on projektiokuvaus. Tavallisimmat projektiot ovat yhdensuuntaisprojektio ja keskusprojektio.
Havainnollinen esimerkki yhdensuuntaisprojektiosta on auringon muodostama varjo. Aurinko on niin kaukana, että valonsäteitä voidaan pitää yhdensuuntaisina. Jos herra Pallon, joka esiteltiin sarjan edellisessä osassa, kolmiulotteisessa maailmassa Tilalassa (Avaruusmaa, Spaceland) olisi ollut samanlainen aurinko, niin hän olisi voinut esittäytyä littiöille varjoaan käyttäen.
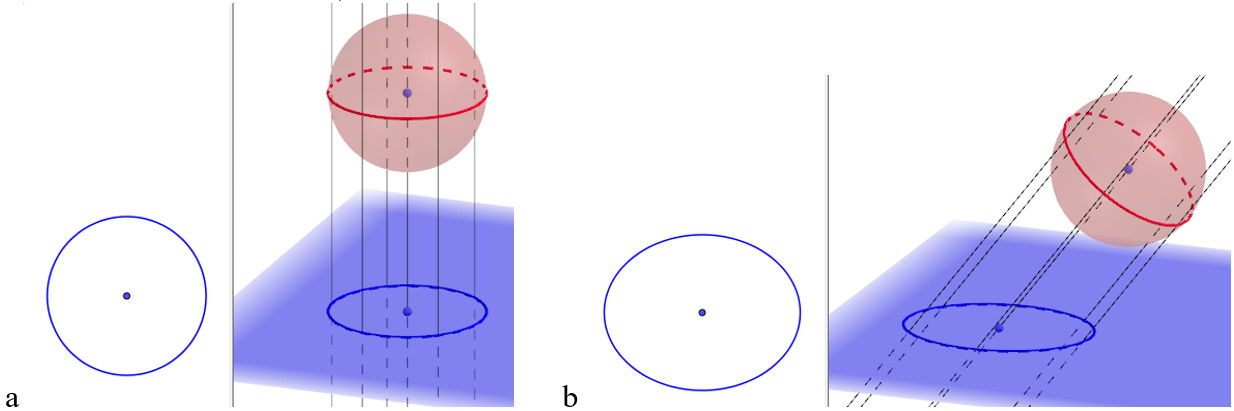
Pallo litistyy ympyräksi kohtisuorassa yhdensuuntaisprojektiossa (a). Vino projektio venyttää kuvan ellipsiksi. [1]
Jos valonlähde on lähempänä, niin varjon muodostumiskuvaus on keskusprojektio. Kuvan koko ja muoto riippuvat valonlähteen etäisyydestä ja valonlähteen suunnasta. Herra Pallolle projektiokuvauksestakaan ei ole suurta hyötyä kolmiulotteisen olemuksensa esittelyssä, sillä kuva pysyy samana, pyöripä hän paikallaan miten tahansa. Varjon venyminen ellipsiksikään ei auta, sillä samanlaisen varjon heittäisi vinoon kääntynyt sivuamisympyräkin.
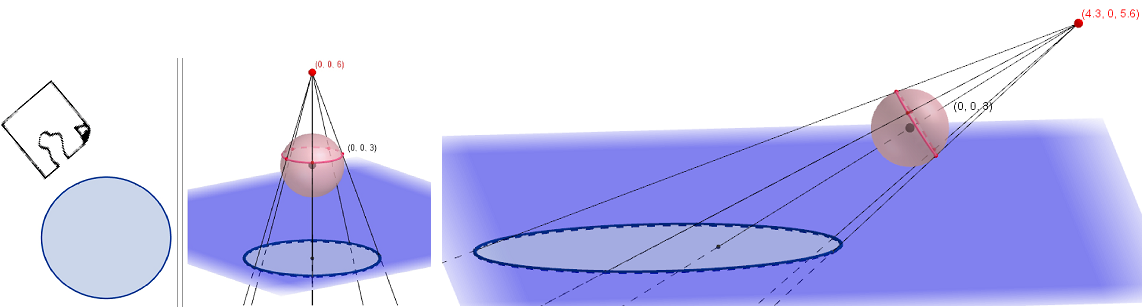
Keskusprojektio kuvaa pallon ympyräksi (vasen kuva) tai ellipsiksi (oikeanpuolimmainen kuva) riippuen valonlähteen suunnasta. Kuvan koko riippuu valonlähteen etäisyydestä. [2]
Keskusprojektion hyöty näkyy jo säännöllisten monitahokkaiden kuvaamisessa. Sen avulla saadaan näkyviin perspektiivivaikutelma, jossa kauempana olevat kappaleen osat näyttävät pienemmiltä kuin projektiotasoa lähempänä olevat.
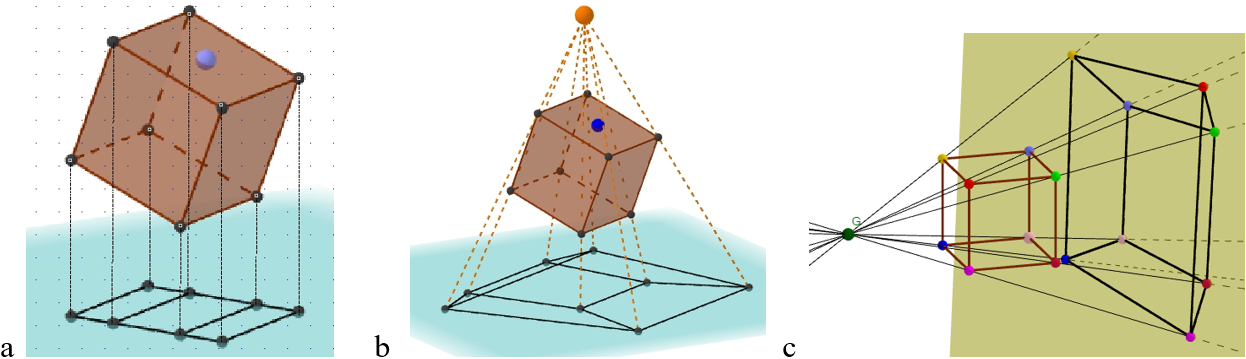
Kuution kuva kohtisuorassa yhdensuuntaisprojektiossa (a [3]) sekä keskusprojektiossa kahdessa eri asennossa (b [3] ja c [4]).
Sarjan seuraavassa osassa katsomme, miten projektiokuvauksia voidaan käyttää neliulotteisten kappaleiden havainnollistamiseen.
Sarja jatkuu.
Sarjan aikasemmat osat:
Perushahmotusta neljännen ulottuvuuden mieltämiseen, osa 1 – Mitä ne ulottuvuudet ovat? (25.3.2020)
Perushahmotusta neljännen ulottuvuuden mieltämiseen, osa 2 – Kahdesta ulottuvuudesta kolmanteen (1.4.2020)
[1] Geogebra-matletti https://www.geogebra.org/m/vbg82f6a
[2] Geogebra-matletti https://www.geogebra.org/m/vwmgw9be
[3] Beck, Kr. Geogebra-matletti https://www.geogebra.org/m/GJuURHsS
[4] Phelps, St. Geogebra-matletti https://www.geogebra.org/m/bpVhcsrh







