Perushahmotusta neljännen ulottuvuuden mieltämiseen, osa 5 – Eroja ja yhtäläisyyksiä

Hyperkuutiosta ja sen useampiulotteisista vastineista saattaa saada sellaisen käsityksen, että geometria on varsin samanlaista neljässä kuin kolmessakin ulottuvuudessa. Tämä ei ole aina totta niin kuin seuraavista esimerkeistä käy ilmi.

Sivuamisluku (engl. kissing number) ilmoittaa, kuinka monta yksikköpalloa voidaan sijoittaa sivuamaan yhtä yksikköpalloa. Huomaa, että 1D-yksikköpallo on jana ja 2D-yksikköpallo on ympyrä.Yksiulotteisessa tapauksessa luku on 2 ja kaksiulotteisessa 6. Nämä voidaan todeta ja perustella yksinkertaisista tasopiirroksista. Kolmessa ulottuvuudessa sivuamisluku on 12, mikä voidaan todeta aika helposti vaikkapa appelsiineilla tai pöytätennispalloilla.

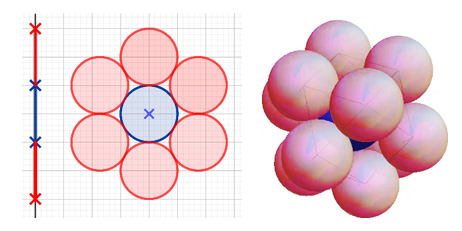
Kolmessa ulottuvuudessa ympärillä olevat pallot eivät kuitenkaan kaikki sivua toisiaan. Ylimääräistä tilaa on niin paljon, että kokeilu ei anna täyttä varmuutta, vaikka jo Newtonkin oli aikanaan sitä mieltä, että 12 on oikea luku. Todistaminen on kuitenkin ihan eri juttu. Sitova todistus saatiin aikaan vasta kaksi ja puoli sataa vuotta myöhemmin vuonna 1953! Siksi ei ole mitään ihmeteltävää siinä, että mitään sääntöä sivuamisluvulle ei osata ajatellakaan. Vain ulottuvuuksille D = 2, 3 ja 4 on yhteinen sääntö 3 · 2^D–1. Neliulotteisessa avaruudessa sivuamisluku on siis 24. Ongelman vaikeutta kuvaa se, että sivuamislukuja ei tunneta edelleenkään tarkasti edellisten lisäksi kuin ulottuvuuksille 8 ja 24 [1], [2]. Sivuavien pallojen määrä kasvaa nopeasti, sillä sivuamisluku on 196 560, kun D = 24.Täsmällisen todistamisen kanssa edellä olevilla havainnollistavilla visualisoinneilla ei ole kuitenkaan mitään  tekemistä [3].

Säännölliset monitahokkaat

Kolmiulotteisessa avaruudessa on tasan viisi erilaista säännöllistä monitahokasta, siis kappaletta, joiden kunkin sivutahkot ovat kussakin tapauksessa samoja säännöllisiä monikulmioita. Tämä perustuu siihen, että muodostaakseen sopen samaan kärkeen liittyvien monikulmioiden kulmien summan pitää olla vähemmän kuin 360^o. Tasasivuisen kolmion tapauksessa mahdollisuuksia on kolme: 3, 4 ja 5. Neliön ja säännöllisen viisikulmion tapauksessa on vain yksi mahdollisuus: kussakin kärjessä kohtaa kolme monikulmiota.

Kaikkien muiden säännöllisten monikulmioiden kulmat ovat liian suuria voidakseen muodostaa sopen. Kolmioista rakentuvissa säännöllisissä monitahokkaissa on sivutahkoja 4, 8 ja 20, neliöistä rakentuvassa 6 ja viisikulmioista rakentuvassa 12. Ne nimetään sivutahkojen lukumäärän mukaan, siis nelitahokas (tetraedri), kuusitahokas (kuutio), kahdeksantahokas (oktaedri), kaksitoistatahokas (dodekaedri) ja kaksikymmentahokas (ikosaedri). Niitä nimitetään Platonin monitahokkaiksi.

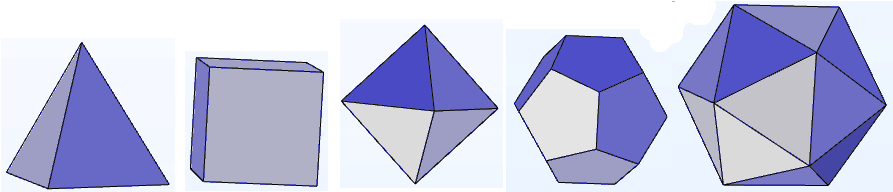
Näillä kaikilla on neliulotteiset vastineet, joiden voidaan ajatella rakentuvan säännöllisistä 3D-monitahokkaista samalla tavalla kuin hyperkuutio rakentuu kuutioista. Ne ovat kaikki kuperia säännöllisiä 4D-monitahokkaita. Neliulotteisessa avaruudessa on vielä kuudeskin monitahokas, jolla on vastaavat ominaisuudet, ja aivan vastoin ennakko-odotuksia säännöllisiä monitahokkaita on vain kolme, kun D > 4.[4] Niiden tutkiminen ei kuitenkaan kuulu enää tämä juttusarjan piiriin, vaikka esimerkiksi hypertetraedrista on hyvä havainnollistava animaatio [5].

Neljässäkään ulottuvuudessa nimitykset eivät ole vakiintuneita, sillä esimerkiksi hyperikosaedrista on käytetty myös nimityksiä 600-solu, tetraplex, heksakosikoron (engl. hexacosichoron), heksakosiedroidi (engl.  hexacosihedroid) ja polytetraedri riippuen siitä, mistä näkökulmasta asiaa on tarkasteltu. Jokaisessa kärjessä kohtaa toisensa viisi tetraedria samalla tavalla kuin ikosaedrin kärjessä kohtaa viisi tasasivuista kolmiota. Luku 600 viittaa siihen, että hyperikosaedrin voidaan ajatella rakentuvan 600 tetraedrista. Kärkiä on 120 ja sivutahkoja 1200. [6]

Solmut

Matemaattisesti solmu on kolmiulotteisen avaruuden suljettu käyrä. Solmuteoriassa myös ympyrää pidetään näin ollen solmuna. Se on (matemaattisista) solmuista yksinkertaisin: triviaalisolmu (engl. unknot, ”epäsolmu”). Toiseksi yksikertaisin on umpisolmu, matemaattisesti apilasolmu [7], [8] (engl. trefoil knot). Solmut voidaan luokitella projektiokuvassa näkyvien risteyskohtien lukumäärän perusteella. Triviaalisolmussa niitä ei ole yhtään ja apilasolmussa 3. Solmujen lukumäärä alkaa kasvaa nopeasti risteyskohtien lukumäärän kasvaessa. Erilaisia solmuja, joissa on viisi risteyskohtaa, on vain kaksi, mutta jo yhdeksän risteyskohtaa omaavia solmuja on 49 erilaista ja kymmenen risteyskohtaa omaavia 165 [9].

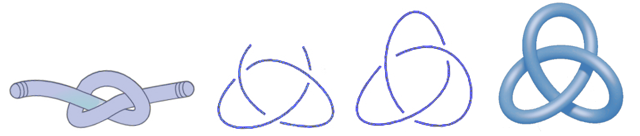
Kaksiulotteisessa avaruudessa ei voi olla solmuja ymmärrettävästä syystä, siis muita kuin triviaalisolmu (ympyrä). Neliulotteisessa avaruudessa ei taas puolestaan ole erilaisia solmuja, sillä siellä kaikki solmut ovat samaa lajia, koska mikä tahansa yksiulotteinen suljettu käyrä, kuinka monimutkaisessa solmussa se näyttäisi olevankaan, voidaan purkaa (avata) ympyräksi (triviaalisolmuksi) käyrää katkaisematta. Eläminen siellä ei siis olisi kovin helppoa, kun edes kengännauhoja ei saisi pitävään solmuun.

Neliulotteisessa maailmassa on kuitenkin solmuja vastaavia objekteja. Ne ovat kaksiulotteisia solmupintoja (engl. knotted surface) [10]. Niiden tarkastelu vie jo paljon yli tämän kirjoitussarjan tavoitteiden, mutta on ehkä hyvä tietää, että yleisestikin D-ulotteisessa avaruudessa on D–2-ulotteisia objekteja, joilla voi olla solmumaisia ominaisuuksia. Jos tiedolla ei ole muuta merkitystä, niin se on ainakin osoitus matematiikan hämmästyttävästä yleistysvoimasta.

Sarjan aikasemmat osat:

Perushahmotusta neljännen ulottuvuuden mieltämiseen, osa 1 – Mitä ne ulottuvuudet ovat? (25.3.2020) Perushahmotusta neljännen ulottuvuuden mieltämiseen, osa 2 – Kahdesta ulottuvuudesta kolmanteen (1.4.2020) Perushahmotusta neljännen ulottuvuuden mieltämiseen, osa3 – Kolmannesta ulottuvuudesta toiseen (8.4.2020) Perushahmotusta neljännen ulottuvuuden mieltämiseen, osa4 – Neljännestä ulottuvuudesta kolmanteen: tesserakti (15.4.2020) Lähteitä ja lisää luettavaa:

[1]  Wikipedia-artikkeli Kissing number osoitteessa https://en.wikipedia.org/wiki/Kissing_number.

[2]  Abel, Z Kissing spheres osoitteessa http://blog.zacharyabel.com/2011/10/kissing-spheres/.

[3]  Musin, O. The kissing number in four dimensions. Annals of Mathematics, 168 (2008), 1–32. Saatavissa myös osoitteesta https://annals.math.princeton.edu/wp-content/uploads/annals-v168-n1-p01.pdf.

[4]  Coxeter, H. S. M. Regular polytopes. Dover, 2017.

[5]  Nosocials: To the 4th Dimension! Imgur-sivustolla https://imgur.com/gallery/I0nyUto.

[6]  Wikipedia-artikkeli 600-cell osoitteessa https://en.wikipedia.org/wiki/600-cell.

[7]  Eronen, S. Solmuteoriaa kombinatorisesti.  Pro gradu -tutkielma, Itä-Suomen yliopisto, 2017. Osoitteessa https://epublications.uef.fi/pub/urn_nbn_fi_uef-20170944/urn_nbn_fi_uef-20170944.pdf

[8]  Lieban, D. ja Phelps, St. Trefoil Knot. Geogebra-matletti osoitteessa https://www.geogebra.org/3d/kvzcezkp.

[9]  Burde, G. ja Zieschang, H. Knots. Walter de Gruyter, 1975.

[10]  Neliulotteisen avaruuden solmupintoja on havainnollistettu esimerkiksi videoissa:

Knotted surfaces –introduction osoitteessa https://www.youtube.com/watch?v=Lx85kIGjIoQ

Knotted surfaces, part 1 osoitteessa https://www.youtube.com/watch?v=nYz3pRk1cCA

Knotted surfaces, part 2 osoitteessa https://www.youtube.com/watch?v=h68AxRiGxBw