Pallopinnan jakoja GeoGebralla
Matematiikan tekeminen on hauskaa, sillä maallikolla on paljon pohtimista ja oppimista sellaisissakin asioissa, jotka ovat matemaatikolle itsestäänselviä. Joskus sattuu kyllä niinkin, että samaa asiaa ei ole kukaan koskaan tarkastellut ihan samasta näkökulmasta. Virikkeen tähän juttuun sain kirjasta Divided Spheres [1]. Halusin kokeilla, millaisia havainnollistuksia saisin aikaan pallopinnan jakamisesta osiin GeoGebralla. Vaikeimmissa kohdissa sain apua suomalaisen GeoGebra-verkoston [2] postituslistan kautta.
Ensin pieni varoituksen sana tavallisille maallikoille, joiden joukkoon luen itsenikin. Verkossa julkaisevien matematiikan harrastajien osaaminen ja kiinnostuksenkohteet ylittävät usein monin verroin sen tason, johon tavallisen ihmisen taidot yltävät. Heidän suorituksiaan voi vain ihailla ja ihmetellä. Olkoot esimerkkeinä meridiaanien ja yhdensuuntaisten piirtäminen pyörähdyskappaleen pinnalle [3] ja lieriöprojektio [4]. Tämä juttu alkaa paljon yksikertaisemmasta.
Pallo voidaan jakaa kahtia keskipisteen kautta kulkevalla tasolla (kuva 1). Jo tässä on pieni haaste, jos ei halua tyytyä siihen, että kuvassa on vain pallo ja taso, vaan että pinnan osat saadaan näkyviin myös erillisinä. GeoGebrassa pallon piirtämiseen on vakiokomento; tarvitsee vain osoittaa keskipiste ja yksi pallon pinnan piste. Puolipallo voidaan piirtää myös tavallisella kahden muuttujan funktiolla
f(x,y)=sqrt(1-x^2-y^2).
Jako-osien piirtämiseen soveltuu vielä paremmin erityinen Pinta-komento:
Pinta(r cos(φ) cos(Θ), r sin(φ) cos(Θ), r sin(Θ), φ, alarajaφ, ylärajaφ, Θ, alarajaΘ, ylärajaΘ),
missä r, φ ja Θ ovat pallogeometrian tavanomaiset pallokoordinaatit [5].
Komennossa on yhdeksän parametria, joten sen opettelu ei kannata yhden kuvan piirtämisen takia. Ensimmäiset kolme ovat avaruuden pisteen (x, y, z) koordinaattien lausekkeet. Seuraavat kuusi määrittelevät alueen ilmoittamalla, millä väleillä olevia arvoja kulmat voivat saada. Teknisesti r, alarajaφ, ylärajaφ, alarajaΘ ja ylärajaΘ ovat komentoon kirjoitettavia vakiolukuja tai ennakolta määriteltyjä lukumuuttujia (liukuja) sekä φ ja Θ komennon sisäisiä parametrimuuttujia.
Tehokkuus on siinä, että samalla komennolla voidaan saada aikaan suuri määrä erilaisia kuvia monista tilanteista vain parametrien arvoja muuttamalla. Esimerkiksi puolipallo saadaan arvoilla
Pinta(r cos(φ) cos(Θ), r sin(φ) cos(Θ), r sin(Θ), φ, 0, 2π, Θ, 0, π / 2),
neljännespallo vaihtamalla φ:n ylärajaksi π ja pallokalotti vaihtamalla Θ:n alarajaksi π / 4 tai jokin muu nollasta poikkeava luku.
GeoGebran omassa opastuksessa Pinta-komennon parametrimuuttujista käytetään nimiä a ja b eikä pallogeometrian kulmatunnuksia. Pallon puolikkaiden tapauksessa on tarpeen luoda vain toinen puolikas, sillä toinen saadaan peilaamalla origon tai xy-tason suhteen. Jos puolipallon z-koordinaattiin r sin(Θ) lisätään lukumuuttuja (liuku), niin puolipallot voi siirtää kauemmaksi pallosta tai toisistaan [6].
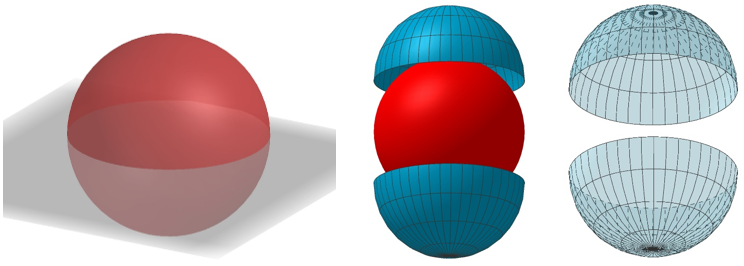
Toisella, edellistä vastaan kohtisuoralla tasolla pallo voidaan jakaa edelleen yhteneviin neljäsosiin ja kolmannella tasolla kahdeksasosiin. Pinta-komento antaa mahdollisuuden jakaa pallon pinta mihin tahansa parilliseen määrään tasaosia (kuva 2). Tämä saattaa näyttää työläältä, mutta jokaista osaa ei tarvitse piirtää erikseen eikä aloittaa muutenkaan joka kerta alusta. Riittää kun luo yhden osan pinta-komennolla ja sitten listan, jossa on tarpeellinen määrä osia kierrettynä z-akselin ympäri:
Jono(Kierto(o, t kiertokulma, zAkseli), t, 1, kuvien_lukumäärä),
missä o on yksi jako-osista, siis pinta-komennolla määritelty pinta, t on komennon sisäinen parametrimuuttuja, kiertokulma ilmoittaa, kuinka paljon o:ta on kierrettävä seuraavan osan piirtämistä varten, zAkseli on kiertoakaseli ja kuvien_lukumäärä tarvittavien kopioiden määrä; esimerkiksi kuudesosajaolle (toinen kuva oikealta seuraavassa).
Jono(Kierto(o, t 120°, zAkseli), t, 1, 2)
ja kolmaskymmeneskahdesosajaolle (oikeanpuolimmainen kuva)
Jono(Kierto(o, t 22.5°, zAkseli), t, 1, 15)
Kiertokulma ja kuvien_lukumäärä voidaan ilmoittaa myös lausekkeina, jos etukäteen on luotu osien määrää säätävä liuku. Jaot saadaan siis vain parametrinarvoja muuttamalla [7]. Lopuksi peilataan tämä lista origon tai xy-tason suhteen.

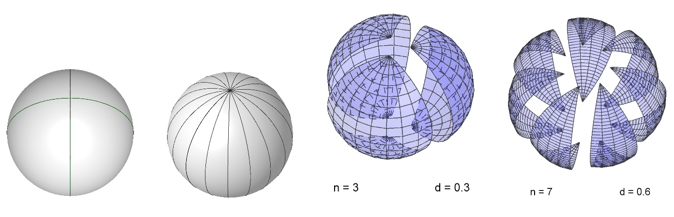
Pallopinta voidaan jakaa samasta pisteestä lähtevillä isoympyrän puolikkailla yhteneviksi pallokaksikulmioiksi millä tahansa osien lukumäärän arvolla (kuvassa 3 esimerkkeinä 4 ja 17, kaksi vasemmanpuoleista). Jos taas halutaan irrottaa osat pallon pinnalta, niin on käytettävä edellä esiteltyä pintakomentoa. Muuta uudelleenmäärittelyä ei tarvita kuin, että toinen kulmamuuttuja Θ (korkeus, deklinaatio) saa arvot väliltä [–π/2, π/2} eli siis navalta navalle.
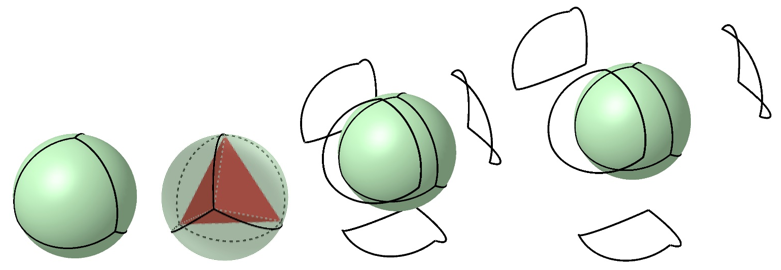
Pallo voidaan jakaa yhteneviin osiin monella muullakin tavalla. Jakoviivoina voivat olla esimerkiksi pallon sisään piirretyn Platonin monitahokkaan kärkipisteitä yhdistävät isoympyrän kaaret. Tällä tavalla saadaan pallopinta jaetuksi 4, 6, 8, 12 ja 20 yhtenevään osaan. Näitä jako-osia en osannut esittää pintakomennolla, mutta jakoviivat saa kyllä erilleen pallon pinnasta [8]. Katsojan on vain kuviteltava näiden kaarien rajaamat pallokolmiot, pallopinnan neljännekset Kuva 4).
Yhtenevien osien lisäksi kiintoisia ovat myös pinta-alaltaan yhtä suuret jako-osat. Muita yhdenmuotoisia kuin yhteneviä kuvioitahan ei pallon pinnalla olekaan. Ilmeisen ratkaisun tarjoaa esimerkiksi pallokalotti, jonka pinta-ala on suoraan verrannollinen kalotin korkeuteen. Kun pallon vastakkaisilta puolilta erotetaan korkeudeltaan säteen puolikkaan korkuiset kalotit ja niiden väliin jäävä vyö jaetaan tasan kahtia, niin siinähän on jako neljäsosiin (kuva 5). Vastaavalla tavalla pallo voidaan jakaa yhdensuuntaisilla, tasavälisillä tasoilla mielivaltaiseen määrään pinta-alaltaan yhtä suuria osia.

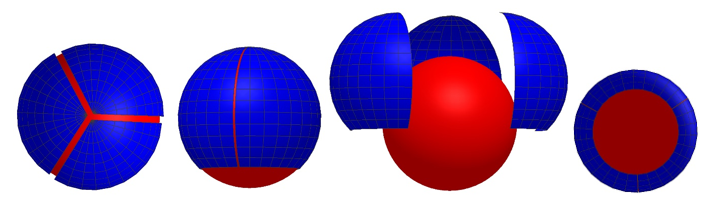
Otetaan mukaan vielä yksi jako pinta-alaltaan neljään yhtä suureen osaan, jotka kaikki eivät myöskään ole yhteneviä [9]. Siniset jako-osat on mallinnettu taas Pinta-komennolla. Nyt ne eivät ole pallokolmioita eivätkä siis edes pallomonikulmioita, koska niiden yksi sivu on pikkuympyrän kaari. Neljäs jako-osa onkin pikkuympyrä (kuva 6).
Jakomahdollisuudet eivät suinkaan lopu tähän, mutta pitäähän jotain jättää lukijankin pohdittavaksi.
Lähteitä ja lisää tutkittavaa:
[1] Popko, E. S. Diveded Spheres. CRC Press, Boca Raton, 2012.
[2] Suomalainen Geogebra-verkosto osoitteessa https://geogebrasuomi.wordpress.com/
Yhteydenotto-alasivulla on ohje postituslistalle liittymisestä.
[3] Lawrence, J. Meridians and Parallels of a Surface of Revolution, Geogebra-materiaali osoitteessa https://www.geogebra.org/m/btn6h3rt
[4] Voráčová, Š. Cylindrical equirectangular projection, Geogebra-materiaali osoitteessa https://www.geogebra.org/m/ukgytBSM
[5] Katso esimerkiksi Korhonen, H. Pallogeometrian perushahmotusta, osa 5 osoitteesta https://www.dimensiolehti.fi/pallogeometrian-perushahmotusta-osa-5/
[6] Geogebra-materiaali Puolipallot osoitteessa https://www.geogebra.org/m/ttgdvusz
[7] Esimerkiksi Geogebra-materiaali Pallopinnan jako kuudestoistaosiin osoitteessa https://www.geogebra.org/m/e8ffhwf4
[8] Geogebra-materiaali Pallopinnan tetraedrijako osoitteessa https://www.geogebra.org/m/wqwp2jgd
[9] Geogebra-materiaali Pallon pinnan neljännes osoitteessa https://www.geogebra.org/m/vt783n6a







