Ohjelmointi ja taide, osa 3: Taidetta laskukaavoilla

Opetus

4.8.2022

Ohjelmoinnin, matematiikan ja taiteen yhdistäminen mahdollistaa projektit, joissa hyödynnetään tekniikkaa luovalla tavalla. Julkaisemme aiheesta kolmiosaisen juttusarjan. Tässä päätösosassa tutkimme, millaista taidetta syntyy matemaattisilla laskukaavoilla.

Ensimmäinen osa Geometriset kuviot (Dimensio 7.7.2022)

Toinen osa Rekursio (Dimensio 21.7.2022)

Pentagrammi monikulmiokomennolla

Kun piirrämme esimerkiksi siniaaltoa, sitä varten joudumme laskemaan paljon x- ja y-koordinaatteja, jotta käyrästä tulisi mahdollisimman kaareva. Kaarevan käyrän piirtämiseen tarvitsemme monikulmiokomentoa, jossa komentojen beginShape() ja endShape(CLOSE) väliin voimme asettaa niin paljon koordinaattipisteitä kuin haluamme. Koordinaattipisteet asetetaan p5js-kielessä vertex(x,y)-komennolla.

Tehdään seuraavaksi ohjelma, jossa ensin asetetaan matematiikan xy-koordinaatisto siirtämällä origo ikkunan keskelle komennolla translate(width/2, height/2); ja peilataan y-koordinaatit ylöspäin komennolla scale(1,-1); Seuraavaksi piirretään keltainen ympyrä ja sen sisälle punainen viisikanta eli pentagrammi. Piirtämistä varten olemme etukäteen laskeneet pentagrammin nurkkapisteet laskukaavoilla x = 200∙cos α ja y = 200∙sin α, missä kulma α saa arvoja: 90°, 162°, 234°, 306°, 378°. Alkukulmaksi on laitettu 90 astetta. Ohjelma, joka piirtää pentagrammin on seuraavanlainen:

function setup() {
  createCanvas(500, 500);       // Ikkunan koko 500 x 500
}

function draw() {
  background(0, 255, 0);        // Taustaväri vihreä
  translate(width/2, height/2); // Origo ikkunan keskelle
  scale(1,-1);                  // Peilaa y-koordinaatit
  fill(255, 255, 0);            // Aseta keltainen täyttöväri
  ellipse(0, 0, 400, 400);      // Piirrä ympyrä
  fill(255, 0, 0);              // Aseta punainen täyttöväri
  beginShape();                 // Aloita monikulmio
    vertex(0, 200);             // Piste (0,200)
    vertex(118,-162);           // Piste (118,-162)
    vertex(-190, 62);           // Piste (-190,62)
    vertex(190, 62);            // Piste (-190,62)
    vertex(-118,-162);          // Piste (-118,-162)
  endShape(CLOSE);              // Lopeta monikulmio
}

Lähde: https://editor.p5js.org/riekkinen/sketches/9nCkaanKR Kun ajat ohjelman, niin lopputulos näyttää tältä:

punainen pentagrammikuvio keltaisessa ympyrässä vihreällä taustalla — Kuva 1: Pentagrammin piirtäminen monikulmiokomennolla.

Sinifunktio

Piirretään seuraavaksi sinifunktio. Lasketaan sinifunktion y-koordinaatit laskukaavalla:

$y = amplitudi\cdot sin(taajuus\cdot x)$

Tässä x-koordinaatti ja kulma ovat käytännössä sama asia, jolloin yhden jakson pituus on 360. Koska olemme määritelleet ikkunan leveydeksi 720, kuvaan mahtuu kaksi jaksoa. Laitamme tämän laskukaavan for-silmukan sisälle eli for-silmukka käy x:n arvot 1…719 läpi ja samalla laskee x-koordinaattia vastaavan y-koordinaatin arvon. Kun haluamme piirtää sinikuvion monikulmiokomennolla, laitamme for-silmukan monikulmion sisäpuolelle. Kokonainen ohjelma sinikuvion piirtämiseksi on seuraavanlainen:

var amplitudi = 150;      // Määritellään muuttuja amplitudi
var taajuus = 2;          // Määritellään muuttuja taajuus
function setup() {
  createCanvas(720, 400); // Määritellään ikkunan koko 720x400
  noFill();               // Asetus, joka poistaa täyttövärin
  strokeWeight(2);        // Viivan paksuus 2
  angleMode(DEGREES);     // Otetaan kulma-asteet 360° käyttöön
}

function draw() {
  background(240);        // Taustaväri vaaleanharmaa
  translate(0,height/2);  // origo 200 px alaspäin 
  scale(1,-1);            // Peilataan y-koordinaatit
  beginShape();           // Aloitetaan monikulmio
    vertex(0,0);          // Ensimmäinen piste (0,0)
    for (var x=1; x < 720; x++) {  
      // For-silmukka, missä x = 1,2,…,719
      var y = amplitudi*sin(taajuus*x); // Laske y-koordinaatti
      vertex(x,y);        // Monikulmion pisteet
    }                     // Lopeta for-silmukka
    vertex(width,0);      // Viimeinen piste (720,0)
  endShape(CLOSE);        // Lopeta monikulmio 
  line(360,200,360,-200); // Piirrä pystyviiva (= yksi jakso)
  line(0,0,width,0);      // Piirrä vaakaviiva
}

Lähde: https://editor.p5js.org/riekkinen/sketches/lAnREf5dx

Kun ajat ohjelman, niin lopputulos näyttää tältä:

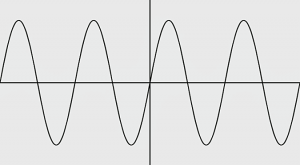
Sinikuvaaja. Ohjelmointi ja taide laskukaavoilla. — Kuva2: Sinikuvaajan piirtäminen monikulmiokomennolla. Kokeile antaa muuttujille amplitudi ja taajuus eri arvoja heti ohjelman alussa, niin sinikuvion muoto muuttuu halutunlaiseksi.

Sydän

Samaa ideaa voimme soveltaa muihin vastaaviin tilanteisiin. Esimerkiksi sydämen muotoisen kuvaajan xy-koordinaatit voidaan laskea laskukaavalla:

$x = 16\cdot sin(t)\cdot sin(t)\cdot sin(t)$ $ y = 13\cdot cos(t)-5\cdot cos(2\cdot t)-2\cdot cos(3t\cdot-cos(4\cdot t)$

missä t on kulma, joka saa arvoja 0°…360°. Lasketaan kuvaajan xy-koordinaatit for-silmukalla, jossasilmukka käy läpi arvot 0:sta 360:een. Laitetaan for-silmukka monikulmiokomennon sisälle ja nyt meillä pitäisi olla monikulmio, joka näyttää sydämeltä. Kokonainen ohjelma on seuraavanlainen:

function setup() {
  createCanvas(400, 400);      // Ikkunan koko 400 x 400
  angleMode(DEGREES);          // Otetaan käyttöön kulma-asteet 360°
}

function draw() {
  var koko = 10;               // Määritellään muuttuja, jolla kuviota 
                               // voidaan skaalata isommaksi.
  background(0);               // Aseta taustaväri mustaksi
  fill(255, 0, 0);             // Punainen täyttöväri
  translate(width/2, height/2);// Origo ikkunan keskelle
  scale(1,-1);                 // Peilaa y:n arvot eli xy-koordinaatisto
  beginShape();                // Aloita monikulmio
      for (var t=0; t < 360; t++) {   // t = 0,1,2,…,360
        var x = 16*sin(t)*sin(t)*sin(t);
        var y = 13*cos(t)-5*cos(2*t)-2*cos(3*t)-cos(4*t);
        vertex(x*koko, y*koko); // Monikulmion piste skaalattuna
      }                         // Lopeta for-silmukka
  endShape();                   // Lopeta monikulmio
}

Lähde: https://editor.p5js.org/riekkinen/sketches/r6EvPHTrF

Kun ajat ohjelman, niin lopputulos näyttää tältä:

Punainen sydän mustalla pohjalla. — Kuva 3: Sydämen xy-koordinaatit on ensin laskettu laskukaavoilla for-silmukan avulla, missä silmukka saa arvoja 0…360, jonka jälkeen pisteet (x,y) on sijoitettu monikulmion sisäpuolelle, joka piirtää halutun kuvion eli sydämen.

Ruusukuviot

Lähes samanlainen piirtämisidea, kuin sydämen laskukaavassa, on myös ruusukuvioissa. Ruusukuviot keksittiin jo 1700-luvulla Italiassa. Ruusukuviot voidaan muodostaa laskukaavoilla.

$r = pituus\cdot cos(k\cdot t)$ $x = r\cdot cos(t)$ $y = r\cdot sin(t)$

missä t saa arvoja 0…360 ja k = n/d. Ruusukuvio muuttaa muotoa, kun k:n arvo muuttuu. K:n arvo on käytännössä kokonaislukujen n ja d suhde. Tehdään ohjelma, jossa liukupalkeilla voidaan muuttaa kokonaislukujen n ja d arvoja ja näemme heti muutoksen kuviossa. Liukupalkki määritellään setup-funktiossa komennoilla:

muuttuja = createSlider(min, max, oletus); muuttuja.position(x, y);

jonka jälkeen draw-funktiossa jollekin toiselle muuttujalle voidaan sijoittaa liukupalkin arvo komennolla:

muuttuja2 = muuttuja.value();

Jotta saamme käyrästä sulavan, niin kulmat kannattaa laskea 0,1-desimaalin välein. Myös tässä ohjelmassa on sama idea eli käyrän pisteet lasketaan for-silmukan avulla ja käyrän pisteet piirrämme monikulmiokomennon avulla. Kokonainen ohjelma ruusukuvioiden piirtämiseksi on seuraavanlainen:

var Liukupalkki_n;   // Määritellään globaalimuuttuja 
var Liukupalkki_d;   // Määritellään globaalimuuttuja

function setup() {
  createCanvas(600, 650);          // Ikkunan koko 600 x 650
  angleMode(DEGREES);              // Kulma-asetus 360° käyttöön
  textSize(20);                    // Tekstin koko 20 px
  Liukupalkki_n = createSlider(1, 50, 4); // Luodaan liukupalkki
  Liukupalkki_n.position(50, 10)          // Liukupalkin paikka
  Liukupalkki_d = createSlider(1, 50, 1); // Luodaan liukupalkki
  Liukupalkki_d.position(350, 10)         // Liukupalkin paikka
} 

function draw() {
  background(0);                   // Taustaväri musta
  var n = Liukupalkki_n.value();   // n saa arvon liukupalkilta
  var d = Liukupalkki_d.value();   // d saa arvon liukupalkilta
  noStroke();                      // Ei reunaviivaa
  fill(255);                       // Täyttöväri valkoinen
  text("n = "+n,210,30);           // Tulosta n:n arvo
  text("d = "+d,510,30);           // Tulosta d:n arvo
  var k = n/d;                     // Laske k = n/d
  translate(width / 2, height / 2);// Origo ikkunan keskelle
  noFill();                        // Ei täyttöä
  stroke(255);                     // Reunaviivan väri valkoinen
  strokeWeight(2);                 // Viivan paksuus 2 px
  beginShape();                    // Aloita monikulmio
    for (var t = 0; t < 360*d; t=t+0.1) { 
    // For-silmukka, missä t = 0,1, 0,2, 0,3, …, 359,9
      var r = 250*cos(k*t);        // Laske r
      var x = r*cos(t);            // Laske x
      var y = r*sin(t);            // Laske y
      vertex(x, y);                // Monikulmion piste
    }                              // Lopeta for-silmukka
  endShape(CLOSE);                 // Lopeta monikulmio
}

Lähde: https://editor.p5js.org/riekkinen/sketches/j81m3Q7IG

Suorita ohjelma ja muuta liukupalkeilla n:n ja d:n arvoja. Ohjelman suoritus voisi olla esimerkiksi seuraavanlainen:

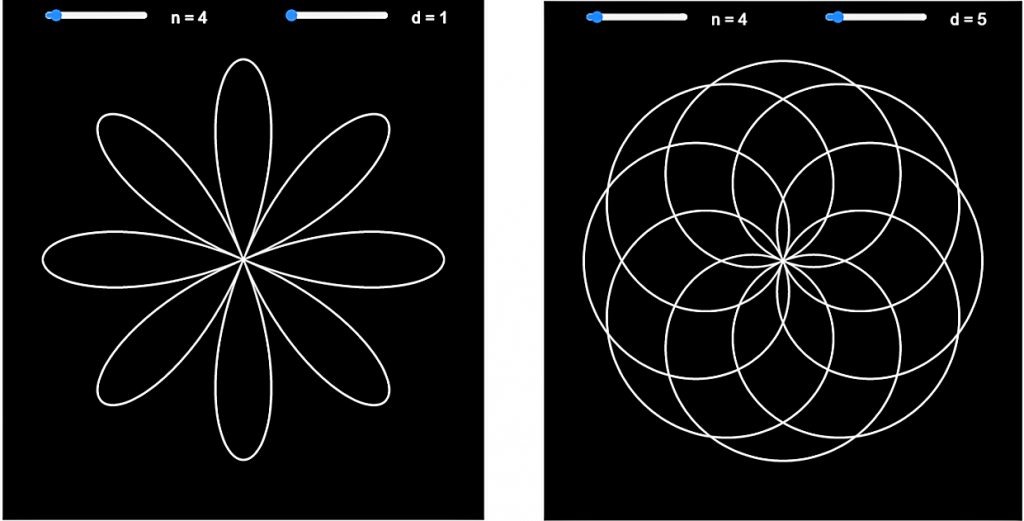
Valkoinen ruusukuvio mustalla pohjalla. Ohjelmointi ja taide laskukaavoilla. — Kuva 4: Kuvassa on esitetty kaksi erilaista mahdollista ruusukuviota

Taidetta laskukaavoilla

Monet taiteilijat ovat innostuneet kehittämään laskukaavoja, joilla saadaan aikaiseksi taidetta. Hamid Naderi Yeganeh on iranilainen yliopistollisen koulutuksen saanut taiteilija, joka yhdistää matematiikkaa ja ohjelmointia luovalla tavalla. Seuraava koodi on kehitetty hänen ideansa pohjalta. Ohjelma piirtää 9000 kappaletta ympyröitä, jotka kulkevat laskettua rataa (x, y) pitkin ja samalla myös ympyrän säde r kasvaa oman laskukaavan mukaisesti.

function setup() {
  createCanvas(800, 800);      // Ikkunan koko
  angleMode(DEGREES);          // Kulma-asteet 360° käytössä
  background(0);               // Taustaväri musta
  translate(width/2, height/2);// Origo ikkunan keskelle
  scale(1,-1);                 // Peilaa y-koordinaatit eli xy-koordinaatisto
  noFill();                    // Ei täyttöväriä
  stroke(255);                 // Reunaviivan väri valkoinen
      for (var t=1; t <= 9000; t++) {  // for-silmukka, missä t = 1,2,3,…,9000
        var r = 380*(1/200.0+1/10.0*pow(sin(64*PI*t/90),6));
        var x = 380*(cos(14*PI*t/90.0)*(1-3/4.0*pow(cos(36*PI*t/90.0), 2)));
        var y = 380*(sin(14*PI*t/90.0)*(1-3/4.0*pow(cos(36*PI*t/90.0), 2)));
        ellipse(x, y, r, r);    // Piirrä ympyrä
      }
}

Lähde: https://editor.p5js.org/riekkinen/sketches/0lauwib1n

Kaavan tarkempi tutkiminen jätetään lukijan pohdittavaksi, mutta idea on hyvin samankaltainen kuin edellisissä esimerkeissä. Tosin tässä ei käytetä monikulmiokomentoa, vaan piirretään 9000 ympyrää, joista kuvio muodostuu. Kun ajat ohjelman niin lopputulos näyttää tältä: