Navigaatiofysiikkaa IV – Sivuutusetäisyys
Tämän kirjoitussarjan aiemmissa osissa [1, 2, 3] tarkasteltiin etäisyyden laskemista majakkaan, silloin, kun majakan valo tulee juuri näkyviin horisontin takaa.
Tässä kirjoitussarjan viimeisessä osassa tarkastellaan toista veneilyesimerkkiä, kahden veneen sivutusetäisyyden laskemista lähtien kahdesta perättäisestä tutkamittauksesta. Valitaan xy-tason origo oman veneen paikkaan ensimmäisen tutkahavainnon hetkellä ja y-akseli veneen kulkusuuntaan.
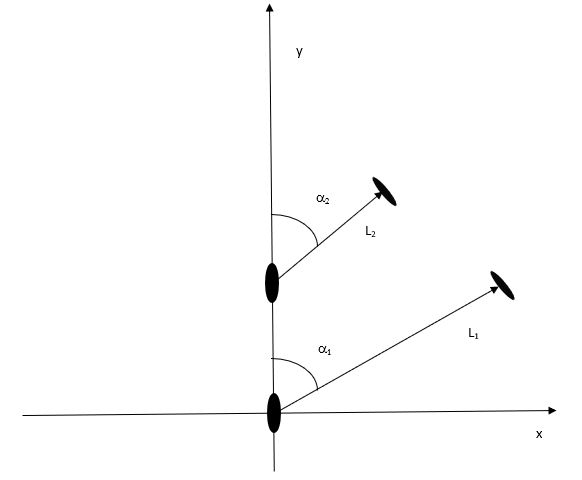
Jos tutkan antamat etäisyydet toiseen veneeseen ovat $L_1$ ja $L_2$ sekä vastaavat keulasuuntimat $\alpha_1$ ja $\alpha_2$ (kts. kuva 1) ja mittausten väli $\Delta t$, on havaitun veneen poikkisuuntainen (x-suuntainen) nopeuskomponentti (kohti oman veneen kulkulinjaa)
| $u_x=\frac{L_1\sin\alpha_1-L_2\sin\alpha_2}{\Delta t}$ | (1) |
Tällöin aika $t_0$, joka kuluu havaitulta veneeltä siihen, kunnes se leikkaa oman veneen kulkulinjan (laskettuna ensimmäisen havainnon hetkestä), on
| $t_0=\ \frac{s}{u_x}\ =\ \frac{L_1\sin\alpha_1}{L_1\sin\alpha_1-\ L_2\ \sin\alpha_2}∆t$ | (2) |
Jos oman veneen nopeus on $v$, on havaitun veneen nopeuskomponentti oman veneen kulkusuunnassa (y-suuntainen nopeuskomponentti)
| $u_y=\frac{\ L_2\cos\alpha_2-L_1\cos\alpha_1}{∆t}+v$ | (3) |
Yhtälöt (2-3) antavat tällöin mahdollisuuden laskea havaitun veneen etäisyyden sen leikatessa oman veneen kulkulinjaa (kuvassa 1. y-akselia):
| $d_0=\ L_1\cos\alpha_1+t_0\left(u_y-\ v\right)\ =\ \frac{L_1L_2\left(\sin\alpha_1\cos\alpha_2-\ \sin\alpha_2\cos\alpha_1\right)}{L_1\sin\alpha_1-\ L_2\sin\alpha_2} $ | (4) |
Käyttämällä osoittajassa erotuskulman siniä voimme kirjoittaa tämän
| $d_0\ =\frac{L_1L_2\sin\left(\alpha_1-\alpha_2\right)}{L_1\sin\alpha_1-\ L_2\sin\alpha_2}$ | (5) |
Jos $d_0>0$ tapahtuu sivuutus keulan edestä, ja vastaavasti jos $d_0 <0$ tapahtuu sivutus perän takaa. Tämä yhtälö pätee vaikka vene lähestyisi takaviistostakin ($\alpha > 90°$). Yhtälö (5) on sopusoinnussa meriteiden sääntöjen varoituksen kanssa, että yhteentörmäys tapahtuu, jos suuntakulma toiseen alukseen ei muutu.
On kuitenkin huomattava, että lyhin etäisyys veneiden välillä, eli merenkulussa käytetty termi CPA (= Closet Point of Approach), ei ole sama, kuin edellä laskettu etäisyys risteävän veneen leikatessa oman veneen kulkusuuntaa, $d_0$. Veneiden etäisyyden laskemiseksi yleisesti käytämme seuraavia lyhennysmerkintöjä:
| \begin{matrix} s_i=\ L_i\sin\alpha_i\\ c_i=\ L_i\cos\alpha_i\\ \end{matrix} | (6) |
Näillä merkinnöillä etäisyyden neliö voidaan lausua
| $d^2=\ \left[s_1-\left(s_1-s_2\right)x\right]^2+\left[c_1-\left(c_1-c_2\right)x\right]^2$ | (7) |
jossa x on skaalattu, dimensioton aikasuure $x=t/∆t$. Aika $t$ on mitattu ensimmäisen tutkahavainnon hetkestä. Ratkaistaan etäisyyden neliön pienin arvo laskemalla derivaatan nollakohta.
| $0=\ -2\left(s_1-s_2\right)\left[s_1-\left(s_1-s_2\right)x\right]-2\left(c_1-c_2\right)\left[c_1-\left(c_1-c_2\right)x\right]$ | (8) |
Minimietäisyyden hetkeksi saadaan tällöin
| $x=\ \frac{s_1\left(s_1-s_2\right)+c_1\left(c_1-c_2\right)}{\left(s_1-s_2\right)^2+\left(c_1-c_2\right)^2}$ | (9) |
Sijoitetaan tämä ääriarvokohta yhtälöön (7). Minimiarvoksi saadaan
| $d_{\min}^2=\ \frac{\left[c_1s_2-c_2s_1\right]^2}{\left(s_1-s_2\right)^2+\left(c_1-c_2\right)^2}$ | (10) |
Sijoitetaan tähän takaisin yhtälön (6) merkinnät. Sievennyksen jälkeen saamme
| $CPA=\ d_{\min}=\ \frac{\left|L_1L_2\left(\sin\alpha_2\cos\alpha_1-\ \sin\alpha_1\cos\alpha_2\right)\right|}{\sqrt{\left(L_1\sin\alpha_1-L_2\sin\alpha_2\right)^2+\left(L_1\cos\alpha_1-\ L_2\cos\alpha_2\right)^2}}$ | (11) |
Käyttämällä tässä taas erotuskulman siniä ja kosinia sekä identiteettiä:
| $\sin^2\alpha+\ \cos^2\alpha=\ 1$ | (12) |
voimme kirjoittaa minimietäisyyden lopuksi
| $CPA=\ \frac{\left|L_1L_2\sin\left(\alpha_1-\alpha_2\right)\right|}{\sqrt{L_1^2+L_2^2-2L_1L_2\cos\left(\alpha_1-\alpha_2\right)}}$ | (13) |
Mikä on taas sopusoinnussa em. meriteiden sääntöjen varoituksen kanssa, että yhteentörmäys tapahtuu, jos suuntakulma toiseen alukseen ei muutu.
Huomaa, että yhtälön (13) neliöjuuressa oleva lauseke on positiivinen luku, koska se on kosinilauseen perusteella kolmas sivu kolmiossa, jossa kaksi sivua ovat $L_1$ ja $L_2$ ja näiden välinen kulma $\alpha_1 – \alpha_2$. Jos kulmasuuntimat ovat samat, on nimittäjän neliöjuuri yhtä kuin etäisyyksien $L_1$ ja $L_2$ erotus.
Lähdeviitteet
[1] T. Toimela, Navigaatiofysiikkaa I, Dimensio, 5.2. 2020
https://www.dimensiolehti.fi/navigaatiofysiikkaa-i-valon-kulun-geometriaa/
[2] T. Toimela, Navigaatiofysiikkaa II, Dimensio, 12.2. 2020
https://www.dimensiolehti.fi/navigaatiofysiikkaa-ii-valon-taittuminen-ilmakehassa/
[3] T. Toimela, Navigaatiofysiikkaa III, Dimensio, 19.2. 2020
https://www.dimensiolehti.fi/navigaatiofysiikkaa-iii-etaisyyden-maarityksesta/
Aloituskuva Phot Daniel Kuruvilla on Unsplash







