Navigaatiofysiikkaa III – Etäisyyden määrityksestä
Navigaatiokirjallisuudessa, esim. [1], löytyvä laskukaava etäisyyden laskemiseksi majakkaan, silloin, kun majakan valo tulee juuri näkyviin horisontin takaa, on
| $s=2{,}08\ \left(\sqrt{\frac{H}{\mathrm{m}}}\ +\ \sqrt{\frac{h}{\mathrm{m}}}\right)\ \mathrm{M}$ | (1) |
jossa $H$ ja $h$ ovat majakan (valon) ja silmän korkeudet merenpinnasta. M = meripeninkulma (Nautical mile) = 1852 m. Tämän kirjoitussarjan ensimmäisessä osassa [2] saimme geometrisellä tarkastelulla tuloksen
| $s=1{,}927\ \left(\sqrt{\frac{H}{\mathrm{m}}}\ +\ \sqrt{\frac{h}{\mathrm{m}}}\right)\ \mathrm{M}$ | (2) |
Yllä oleva geometrinen tulos poikkeaa yhtälöstä (1) noin 8
$\cos\theta=\ \frac{R}{r}\ \cdot\ \frac{1+\ a\rho_0}{1+\ a\rho_0e^{\left(-\ \frac{\rho_0gT_0}{p_0\alpha}+1\right)\ln\frac{1}{1-\ \alpha\ (r-R)/T_0}}}$ (3)
Tämä yhtälö siis vastasi tilannetta, jossa valonsäde sivuaa yhdessä kohtaa meren pintaa, eli $\theta = 0$, kun $r=R$.
Oletetaan tässä normaali ilmanpaine $p_0=101{,}325\ \mathrm{kPa}$ ja lämpötilaa $T_0=+25\ °\mathrm{C}$ vastaava (ideaalikaasun) tiheys $\rho_0=1{,}185\ \mathrm{kg/m^3}$, saadaan $b=\frac{\rho_0g}{p_0}=\ 0{,}000115\ 1/\mathrm{m}$. Vakiolle $\alpha$ käytämme arvoa $\alpha=0{,}0065\ \mathrm{K/m\ }$ [4, 5]. Edelleen ilman taitekertoimen tiheysriippuvuuden vakiolle a käytämme lukuarvoa $a=0{,}000228\ \mathrm{m}^3/\mathrm{kg}$ [4].
Hyödynnämme tätä yhtälöä (3) etäisyyden laskemiseksi majakkaan. Etäisyyden määrittämiseksi tarvitaan korkeus ($h = r-R$) valon maan keskipisteen suhteen kiertyneen kulman funktiona. Nyt valon kulkusuunnan (vaakatason kanssa muodostaman) kulman $\theta$ tangentti on kulkukäyrän kulmakerroin
| $\tan\theta=\ \frac{dy}{dx}$ | (4) |
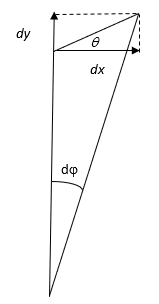
Siirryttäessä karteesisesta xy-koordinaatistosta napakoordinaatteihin ($r$, $\varphi$) pätee (lähtöpisteen ollessa y-akselilla) infinitesimaalisella tarkkuudella $dy\ =\ dr$ ja $dx=rd\varphi$ (kts. kuva 1.). Joten
| $\frac{dr}{d\varphi}=r\tan\theta=r\ \frac{\sqrt{1-\mathrm{\cos}^2\theta\ }}{\cos\theta}=\ \frac{r\ \sqrt{r^2-\ R^2\ \left(f(r-R)\right)^2}}{R\ f(r-R)}$ | (5) |
jossa tangentti on lausuttu kosinin avulla ja funktio $f(x)$ on yhtälön (3) perusteella
| $f\left(x\right)=\ \frac{1+\ a\rho_0}{1+\ a\rho_0e^{\left(-\ \frac{b\ T_0}{\alpha}+1\right)\ln\frac{1}{1-\ \alpha\ x/T_0}}}$ | (6) |
Yhtälöstä (5) saadaan integroitua etäisyys isoympyrää pitkin
| $s=R\varphi=\int_R^r\frac{R^2\ f\left(r-R\right)dr}{r\ \sqrt{r^2-\ R^2\ \left(f(r-R)\right)^2}}=\ \int_0^H\frac{R^2\ f\left(x\right)dx}{(R+x)\ \sqrt{(R+x)^2-\ R^2\ \left(f(x)\right)^2}}$ | (7) |
Ottaen tällöin huomioon, että $H\ll\ R$ ja $bH\ll1$, kehitetään integroitava muuttujan $x$ johtavaan kertalukuun (vrt. McLaurinin sarja). Siten saadaan
| $s\cong\ R\ \int_0^H\frac{dx}{\sqrt{2Rx-2R^2a\rho_0\left(b-\ \alpha/T_0\right)x/(1+a\rho_0)}}=\ \frac{\sqrt{2RH}}{\sqrt{1-Ra\rho_0\left(b-\ \alpha/T_0\right)/\left(1+a\rho_0\right)}}$ | (8) |
Kirjoitetaan yhtälö (8) meripeninkulman M avulla kuten tämän kirjoitussarjan ensimmäisessä osassa [2]
| $s=\ \sqrt{\frac{360\cdot60}{1852\ \pi}\ }\cdot\ \frac{1}{\sqrt{1-Ra\rho_0\left(b-\ \alpha/T_0\right)/\left(1+a\rho_0\right)}}\ \cdot\ \sqrt{\frac{H}{\mathrm{m}}}\ \mathrm{M}$ | (9) |
Yhtälössä (9) ensimmäinen kerrointermi on arvoltaan 1,927, toinen termi puolestaan on 1,091, jolloin yhteensä
| $s=2{,}10\ \mathrm{M}\sqrt{\frac{H}{\mathrm{m}}}$ | (10) |
Valon taittumisen vaikutus etäisyysmittaukseen on huomattavan suuri, noin 9
$90°-θ≅90°$ (11)
Matemaattisesti tämän taitekertoimen pienen muutoksen aiheuttaman vaikutuksen valon kulkukulmaan näkee kirjoitussarjan aiemmassa osassa [3] johdetusta valon kulkusuunnan ja taitekertoimen välisestä relaatiosta:
| $d\theta=\ \frac{dn}{n\tan\theta}\ \cong\ \frac{dn}{n \theta}$ | (12) |
jolloin hyvin pienikin taitekertoimen $dn$ muutos aiheuttaa suhteellisen ison kulmamuutoksen, koska kulma $\theta $ itsessään on pieni.
Kerroin yhtälössä (10) on prosentin suurempi kuin, mitä kirjallisuudessa [1] on annettu. Tässä on kuitenkin huomattava, että kertoimen tarkka arvo riippuu lämpötilasta ja paineesta ja lisäksi maan gravitaatiokentästä purjehduspaikalla. Edellä on oletettu lämpötilan olevan $+25\ °\mathrm{C}$, ilmanpaineen normaali ja painovoimakiihtyvyys ns. normipaikkakunnalla, $g=9{,}80665\frac{\mathrm{m}}{\mathrm{s}^{\mathrm{2}}}$.
Etäisyyden voisikin siten kirjoittaa lopuksi (huomioiden myös silmän korkeuden $h$):
| $s=\ \frac{1{,}927}{\sqrt{1-a\ R\cdot\frac{pM_{ilma}\ }{R_mT^2}\left(\frac{gM_{ilma}}{R_m}-\ \alpha\right)/\left(1+a\ \frac{pM_{ilma}\ }{R_mT}\right)\ }}\ \cdot\ \left(\sqrt{\frac{H}{\mathrm{m}}}\ +\ \sqrt{\frac{h}{\mathrm{m}}}\right)\ \mathrm{M}$ | (13) |
Tämän etäisyyskaavan kerroin on isompi korkeapaineen vallitessa. Isompiin kertoimiin päädytään myös, jos tyydytään purjehtimaan vain korkeilla pohjoisilla tai eteläisillä latitudeilla, jolloin lämpötila $T$ on yleensä alempi ja myös painovoimakiihtyvyys $g$ on keskimääräistä suurempi.
Majakan etäisyyden laskemiseksi tarkasti pitäisi siis lukea merikortista majakan valon korkeus ($H$), määrittää silmän korkeus meren pinnasta ($h$), selvittää painovoimakiihtyvyys purjehduspaikalla ($g$) ja lukea ilmapuntari ($p$) sekä lämpömittari ($T$).
Lähdeviitteet
[1] Suomen Navigaatioliitto: Veneilijän merenkulkuoppi II, Rannikko-navigointi, Unigrafia Oy, Helsinki, 2013
[2] T. Toimela, Navigaatiofysiikkaa I, Dimensio, 5.2. 2020
https://www.dimensiolehti.fi/navigaatiofysiikkaa-i-valon-kulun-geometriaa/
[3] T. Toimela, Navigaatiofysiikkaa II, Dimensio, 12.2. 2020
https://www.dimensiolehti.fi/navigaatiofysiikkaa-ii-valon-taittuminen-ilmakehassa/
[4] David R. Lide (ed.), Handbook of Chemistry and Physics, 87th edition, Taylor Francis Group, 2006
[5] Inkinen-Tuohi, Momentti 1, Insinöörikoulutuksen fysiikka, Otava, 1999
Aloituskuva Phot Daniel Kuruvilla on Unsplash







