Navigaatiofysiikkaa II – Valon taittuminen ilmakehässä
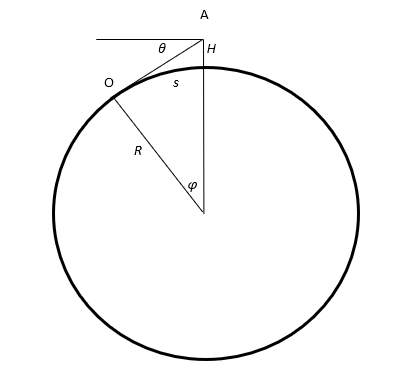
Tämän kirjoitussarjan ensimmäisessä osassa [1] laskimme majakan etäisyyttä tilanteessa, kun majakan valo tulee juuri näkyviin horisontin takaa. Oletimme laskussa valon kulkevan viivasuoraan. Tämän oletuksen mukaan kulma $\theta$, jonka valonsäde muodostaa vaakatason (kussakin kohdassa alapuolella olevan maan pinnan kanssa yhdensuuntaisen tason) kanssa, on sama kuin valon maan keskipisteen suhteen kiertämä kulma $\varphi$ (kts. kuva 1)
| $\theta=\varphi=\ \cos^{-1}\frac{R}{r}$ | (1) |
jossa $r$ on maan keskipisteestä mitattu etäisyys ($r = R+H$). Eli maan keskipisteestä mitatulle etäisyydelle $r$ ja valon suuntakulmalle $\theta$ pätee relaatio
| $\cos\theta=\ \frac{R}{r}$ | (2) |
Differentioimalla yhtälö (2) puolittain saadaan tällöin valon edetessä korkeuden $r$ ja kulman $\theta$ muutoksille
| $-\ \sin\theta\ d\theta= -\frac{R}{r^2}\ dr=\ -\ \cos\theta\ \frac{dr}{r}$ | (3) |
Supistetaan miinusmerkki yhtälöstä (3) ja jaetaan $\cos\theta$:lla, jolloin saadaan
| $\tan\theta d\theta_1= \frac{dr}{r}$ | (4) |
Kulman $\theta$ ja etäisyyden $r$ välinen relaatio muuttuu, kun otetaan huomioon valon taittuminen. Tarkastellaan valon taittumista infinitesimaalisen pienessä ilmakerroksessa. Snellin laista saadaan (kts. kuva 2)
| $n\left(r\right)\cos\theta=n\sin\left(90°-θ\right)=\left(n+dn\right)\sin\left(90°-\theta-d\theta\right)=\left(n+dn\right)\cos\left(\theta+d\theta\right)$ | (5) |
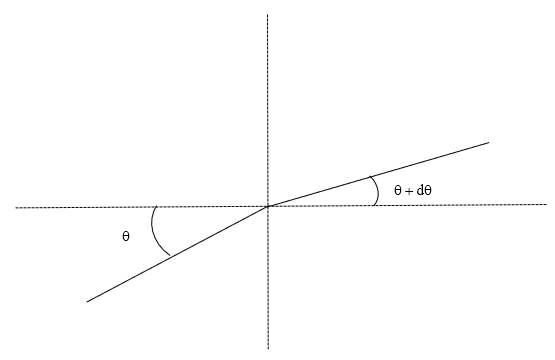
Käyttäen summakulman kosinia saadaan
| $n\ \cos\theta= \left(n+dn\right)\ \left(\cos\theta\cos d\theta-\sin\theta\sin d\theta\right)$ | (6) |
Nyt infinitesimaalisille muutoksille $d\theta$ pätee $\cos d\theta=1$ ja $\sin\ d\theta=d\theta$, jolloin saadaan
| $d\theta_2= \frac{dn}{n\tan\theta}$ | (7) |
Ilman taitekerroin $n$ riippuu ilman tiheydestä [2]
| $n=1+a\rho$ | (8) |
Vakiolle $a$ löytyy kirjallisuudesta hieman toisistaan poikkeavia arvoja. Alonso-Finn [2] antaa lukuarvon $a=0{,}00024\ \mathrm{\frac{m^3}{kg}}$. Taulukkokirjan Handbook of Chemistry and Physics [3] tulosten saamiseksi on oletettava lukuarvo $a=0{,}000228\ \mathrm{\frac{m^3}{kg}}$. Ilman tiheys $\rho$ taasen riippuu korkeudesta [4]
| $\rho= \rho_0\ e^{-\frac{\rho_0gh}{p_0}}\ \ \ \ {,}\ \ \ \ h=r-R$ | (9) |
Tämä yksinkertaistettu yhtälö (9) kuitenkin yliarvioi tiheyden ja sen mukana valon taitekertoimen muutosta korkeuden funktiona. Se ei ota huomioon lämpötilan riippuvuutta korkeudesta. Nyt ideaalikaasun tilanyhtälön perusteella ilman tiheys on
| $\rho=\frac{pM_{ilma}}{R_mT}$ | (10) |
Jossa $R_m$ on moolinen kaasuvakio ja $M_ilma$ on ilman moolimassa.
Kahden (tai useamman) muuttujan funktion $f(x,y)$ muutos muuttujien $x$ ja $y$ infinitesimaalisen pienissä muutoksissa voidaan lausua kokonaisdifferentiaalin avulla
| $\Delta f\approx df\left(x{,}\ y\right)=\frac{∂f}{∂x}dx+\frac{∂f}{∂y}dy$ | (11) |
jossa $\frac{∂f}{∂x}$ on funktion $f(x,y)$ osittaisderivaatta muuttujan $x$ suhteen (normaali derivaatta niin, että muuttujaa $y$ käsitellään vakiona). Kirjoitetaan tiheyden (10) kokonaisdifferentiaali paineen ja lämpötilan avulla
| $\rho=\frac{M_{ilma}}{R_mT}\ dp-\ \frac{M_{ilma}p}{R_mT^2}\ dT$ | (12) |
Paineen muutos aiheutuu aerostaattisen paineen muutoksesta (vrt. hydrostaattinen paine)
| $dp= -\rho\ g\ dh$ | (13) |
Lämpötilalle voidaan olettaa lineaarinen riippuvuus korkeudesta
| $T=\ T_0- \alpha\ h$ | (14) |
jossa $\alpha=0{,}0065\ \mathrm{\frac{K}{m}}$ [3, 4]. Lämpötilan muutos yhtälössä (12) on siis
| $dT= -\alpha\ dh$ | (15) |
Tiheyden muutos voidaan lausua siten korkeuden avulla
| $d\rho= – \frac{M_{ilma}g\rho}{R_mT}\ dh+\ \frac{M_{ilma}p}{R_mT^2}\alpha\ dh$ | (16) |
Eli
| $\frac{d\rho}{\rho}=\ \left(-\frac{M_{ilma}g}{R_m}+\alpha\right)\ \frac{dh}{T_0-\alpha\ h}$ | (17) |
Integroidaan tämä puolittain ja ratkaistaan tiheys. Yhtälön (9) antama tiheyden korkeusriippuvuus korvautuu tällöin lausekkeella
| $\rho=\ \rho_0e^{\left(-\ \frac{g\ M_{ilma}}{R_m\alpha}+1\right)\ln\frac{T_0}{T_0-\ \alpha h}}\ =\ \ \ \rho_0e^{\left(-\ \frac{\rho_0gT_0}{p_0\alpha}+1\right)\ln\frac{1}{1-\ \alpha h/T_0}}$ | (18) |
Ottamalla raja-arvon $\alpha \rightarrow 0$ voimme todeta, että yhtälö (18) palautuu aiempaan yhtälöön (9). Käyttämällä kuitenkin tarkempaa yhtälöä (18) saamme yhtälön (8) taitekertoimelle lausekkeen
| $n\left(r\right)=1+a\rho_0e^{\left(-\ \frac{\rho_0gT_0}{p_0\alpha}+1\right)\ln\frac{1}{1-\alpha\left(r-R\right)/T_0}}$ | (19) |
jossa käytämme vakiolle $a$ lähteen [3] arvoa $a=0{,}000228\ \mathrm{\frac{m^3}{kg}}$. Nyt yhtälön (7) perusteella
| $d\theta_2= \frac{1}{n\tan{\theta}} \frac{dn}{dr}\ dr$ | (20) |
Yhdistämällä geometriasta seuraava $d\theta_1$, yhtälö (4), ja Snellin laista aiheutuva $d\theta_2$, yhtälö (20), saadaan
| $\tan\theta d\theta=\ \left(\frac{1}{r}-\frac{1}{n}\frac{dn}{dr}\right) dr$ | (21) |
Integroimalla tämä puolittain
| $\int_{0}^{\theta}{\tan{w}dw}= \int_{R}^{r}{\left(\frac{1}{z} – \frac{1}{n} \frac{dn}{dz}\right) dz}$ | (22) |
saadaan
| $-\mathrm{\ln}\cos\theta=\ln\frac{r}{R}+\ln n\left(r\right)-\ln n\left(R\right)$ | (23) |
Sijoittamalla taitekerroinfunktio (19) yhtälöön (23) saadaan valon kulkusuunnan maan pinnan kanssa yhdensuuntaisen tason kanssa muodostaman kulman riippuvuudelle maan keskipisteestä mitatusta etäisyydestä $r$ yhtälö
| $\cos{\theta}=\ \frac{R}{r} \cdot \frac{1+\ \alpha \rho_0}{1+\ \alpha\rho_0e^{\left(-\ \frac{\rho_0gT_0}{p_0\alpha}+1\right)\ln{\frac{1}{1-\alpha\left(r-R\right)/T_0}}}}$ | (24) |
Tämä tarkempi yhtälö korvaa valon suoraviivaisen kulun oletuksen mukaisen yhtälön (2). Käytämme tätä yhtälöä (24) tämän kirjoitussarjan kolmannessa osassa aluksen etäisyyden määrittämiseen majakasta.
Lähdeviitteet
[1] T. Toimela, Navigaatiofysiikkaa I, Dimensio, 5.2. 2020
https://www.dimensiolehti.fi/navigaatiofysiikkaa-i-valon-kulun-geometriaa/
[2] Marcello Alonso, Edward J. Finn: Fundamental University Physics II, Addison-Weseley, 1967
[3] David R. Lide (ed.), Handbook of Chemistry and Physics, 87th edition, Taylor Francis Group, 2006
[4] Inkinen-Tuohi, Momentti 1, Insinöörikoulutuksen fysiikka, Otava, 1999
Aloituskuva Phot Daniel Kuruvilla on Unsplash







