Matriisimekaniikkaa yleistajuisesti. Osa 3: Kvanttiloogiset operaatiot

Johdanto

Kahdessa kirjoituksessani (Arvi Hakanen, Dimensio 16.11.2021 ja 17.11.2022) lähestyin matriisimekaniikkaa ensiksi fotonien kontekstissa ja toiseksi fermionien kontekstissa. Jälkimmäisessä (Matriisimekaniikkaa yleistajuisesti. Osa 2) etenin yhden hiukkasen kaksitilasysteemistä kaksihiukkassysteemiin, jollainen on esimerkiksi He-atomin elektronien kaksoisspinsysteemi. Sitä voidaan pitää prototyyppinä kaikille muille elektronien pariutumisille atomeissa, molekyyleissä ja vaikkapa suprajohteissa. Kaksitilasysteemiin ja kaksihiukkassysteemiin liittyvästä matriisimekaniikasta minun on nyt tarkoitus edetä yhden ja kahden kubitin kvanttiloogisiin operaatioihin, joita matriisimekaniikan ansiosta voidaan tarkastella matriisioperaatioina.

Kvanttiloogiset operaatiot voidaan paitsi esittää matriisein myös visualisoida käyttäen Blochin palloa, jossa kubitin puhdas superpositiotila on pallopinnan pisteen paikkavektori. Kvanttilooginen operaatio voi olla esimerkiksi kannan vaihto, jolla yksiulotteisesta tilavektorista tehdään symmetrisesti kaksiulotteinen. Ensimmäinen operaatio on (Paulin X-matriisilla tehtävä) NOT-operaatio, joka pyöräyttää alkutilaansa alustetun kubitin tilavektorin kärjen pallon pohjoisnavalta etelänavalle. Toisilla (Y-, Z-, S- ja T-operaatioilla) taas muokataan vaihetekijää, jota hyödynnetään tietyissä laskenta-algoritmeissa, joissa kubittien vaiheet vuorovaikuttavat. Kubitin mittauksen tuloksena amplitudit ja niihin liittyvät todennäköisyydet luetaan. Vaikka tavoitellaan yleistajuista tyyliä, pohjatietoina olisi hyvä kerrata kompleksiluvut ml. kompleksivektorin käsite, jotta Blochin pallosta saadaan havainnollinen. Netistä löytyy simulaatio, jossa kubitin puhtaaseen superpositiotilaan voidaan soveltaa kvanttiloogisia operaatioita (X-, Y-, Z-, H-, S- ja T-matriisit): [1]

Yhden kubitin operaatioista esitän sovelluksen, joka on jo kyetty verifioimaan käyttäen LUMIQ-supertietokoneen bitti- ja kubittilaskennan rajapintaa [2]. Yhteen kubittiin liittyvän kvanttilaskennan avulla on mahdollista tuottaa aidosti satunnainen jono nollia ja ykkösiä. Toimiva kvanttitietokone vaatii monien käytännön ongelmien ratkaisemista, esim. kubitin superposition romahduttava lukeminen on eri asia kuin kirjoittaminen, jossa kubitin/kubittien superpositioon tehdään matriisioperaatioita. Useamman kubitin rekisteri eroaa tavanomaisesta bittirekisteristä siinä, että kubitteja voidaan lomittaa yhteen, jolloin niiden välille saadaan yhteyksiä, joita laskennassa hyödynnetään. Kubittisysteemi tai sen koherenssi on saatava säilymään laskentasyklin ajan, kunnes tietyn kubitin mittaus tuottaa halutun tuloksen. Laskentasykli tyypillisesti toistetaan useita kertoja, jotta sen tulos tarkentuu. Lukeminen/mittaus on irreversiibeli prosessi siinä missä laskenta on reversiibeliä (palautuvaa). Matriisien avulla havainnollistetaan sitä, miten laskenta sisältää mahdollisuuden takaisinlaskentaan eli on palautuvaa.

Kahteen kubittiin liittyy olennaisesti kvanttilomittumisen (tai kvanttikietoutumisen) käsite. Lomittamalla kubitit voidaan saada aikaan maksimaalisesti lomittuneet kubitit, jolloin toisen tilan määritys merkitsee samalla toisen tilan määritystä. Maksimaalisesti lomittuneet ovat esimerkiksi He-atomin elektronit perustilassa… lomittuminen on siis lähtökohtaisesti luonnollinen ilmiö. Kvanttilaskennan kontekstissa se on tie monen kubitin laskentaan, johon tarkoitukseni on edetä artikkelin loppupuolella. Monen kubitin laskennalla tunnetuilla klassista ja kvanttilaskentaa yhdistävillä algoritmeilla voidaan saavuttaa monia kilpailuetuja klassiseen bittilaskentaan verrattuna (jopa murtaa alkulukusalauksia). Lomittaminen voidaan tehdä esimerkiksi siten, että kahden kubitin tilan lukeminen ei romahduta kolmannen kubitin superpositiota vaan se säilyy (viestikubitti). Kolmen kubitin lomittamisen tarjoamia mahdollisuuksia tarkastelen kvanttiteleportaation esimerkin avulla.

Kvanttilaskennan lyhyt historia

Kvanttilaskennan (ja kvantti-ICT:n) alkutahdit kirjoitettiin noin sata vuotta sitten, kun Wolfgang Pauli otti käyttöön (myöhemmin spininä tunnetun) binäärisen kvanttiluvun atomien elektronirakenteen kuvauksessa. Hän kehitti Paulin spinmatriiseina eli spinoreina tunnetut X-, Y- ja Z-matriisit, jotka ovat tärkeitä Blochin palloon (Kuva 1) liittyviä kvanttiloogisia operaatioita. Kolmiulotteisen spinvektorin mahdollisia orientaatioita voidaan kuvata 2×2 matriiseilla, kunhan niihin hyväksytään tarvittaessa kompleksilukukertoimia. Matriisin kertoimien kompleksisuus lisää kolmannen ulottuvuuden siihen, että kubittien tilavektorit esitetään aina kaksiulotteisen kannan lineaarikombinaatioina. Tämän oivalluksen ansiosta laskennassa käytettäviä dimensioita voidaan redusoida ja saadaan sääntö, jonka mukaan operointi n:n kubitin rekisteriin vaatii 2ⁿx2ⁿ matriisin. Kahden kubitin lomittamiset onnistuvat 4×4 matriiseilla. Fysikaalisesti matriisin kertoimien kompleksisuus tuo spinin kuvaukseen mukaan vaihetekijän. Kaikkien primitiivisin kvanttilaskenta tapahtuu atomeissa ja molekyyleissä luonnostaan. Jos elektroni osaisi puhua, se voisi sanoa toiselle (elektronille He-atomissa): “Ota sinä spinvektorisi arvoksi ½, niin minä olen -½ ja silloin mahdumme molemmat tuolle samalle pallosymmetriselle s-orbitaalille”…”tiedän, tämä voi kuulostaa tylsältä, mutta koska olemme kvanttimekaanisia hiukkasia, meillä on se toinenkin mahdollinen asento samanaikaisesti, ja yhteinen tilamme on lomittunut Bellin tila $\left.\ |\mathrm{\Psi}^-\right\rangle$”…

Ensimmäisessä virittyneessä tilassa He-atomien elektronien suorittama ”laskenta” tuottaa em. singlettitilan lisäksi triplettitilan, joka onkin jo “liikaa” universaalille (eli kvanttiloogisten operaatioiden yhdistelminä muodostettavien algoritmien) kvanttilaskennalle. Universaalissa kvanttilaskennassa hyödynnetään mm. kahden kubitin Bellin lomittuneita tiloja, joihin palataan tuonnempana. Kubitteihin vangittujen hiukkasten ei ole sallittua (tai toivottua) vaihtaa paikkaa luonnollisten triplettitilojen tapaan. Kubitit/hiukkaset saadaan vaihtamaan tilaa, kun niihin operoidaan 4×4 SWAP-matriisilla. Kaksidimensionaalisten “anyonien” triplettitiloja sitä vastoin voidaan teoriassa käyttää tulevaisuuden kvanttilaskennassa, ”jos niiden (letittyvä) aaltofunktio tallettaa tiedon kustakin triplettitilalle ominaisesta identtisten hiukkasten vaihdoksesta”. Tämä viimeinen virke on melko vapaasti käännetty Wikipedia-artikkelista ”Anyon”. Tavallisilla fermioneilla kokonaisaaltofunktio on antisymmetrinen, jolloin identtisten hiukkasten vaihdoksessa merkin täytyy vaihtua spinosassa, jos avaruusosa on symmetrinen. Tai sitten avaruusosan on oltava antisymmetrinen, jos spinosassa merkki ei vaihdu.

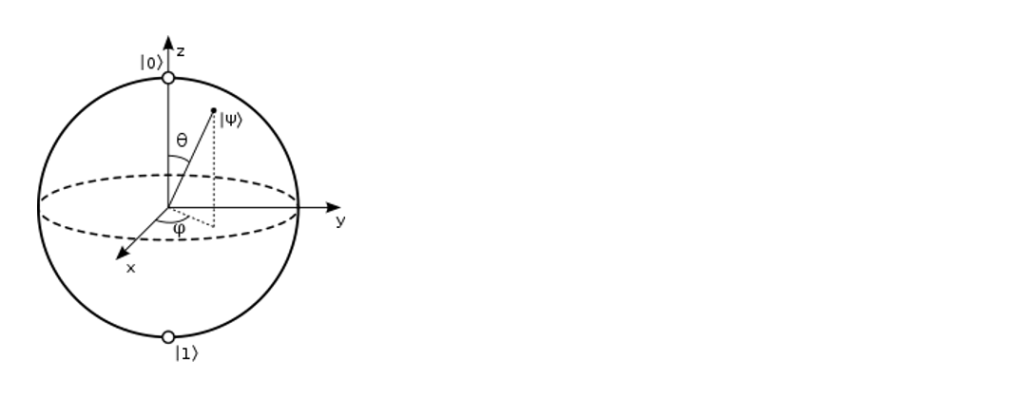
Lähdetään liikkeelle Blochin pallosta ja siitä, että spinin binäärisyys on oikeastaan laskentatulos. Laskenta alustetaan niin, että kubitit asetetaan tilaan $\left.\ |0\right\rangle$. Niinpä kantaa $\left.\ |0\right\rangle,\ \left.\ |1\right\rangle$ kutsutaan laskennalliseksi. Tässä kannassa kubitin tilavektori $\left.\ |\psi\right\rangle=\left.\ 1|0\right\rangle+\left.\ 0|1\right\rangle$ osoittaa Blochin pallon pohjoisnavalle ja tilavektori $\left.\ |\psi\right\rangle=\left.\ 0|0\right\rangle+\left.\ 1|1\right\rangle$ etelänavalle. Tila on fysikaalinen silloin, kun tilavektorin pituus on yksi. Yleisesti tilavektori $\left.\ |\psi\right\rangle=\left.\ \alpha|0\right\rangle+\left.\ \beta|1\right\rangle$ voidaan kirjoittaa kahden kulman avulla seuraavasti:

$$\left.\ |\psi\right\rangle=e^{i\gamma}(\cos{\frac{\theta}{2}\left.\ |0\right\rangle}+e^{i\varphi}\sin{\frac{\theta}{2}\left.\ |1\right\rangle}) \qquad \qquad \qquad \qquad \qquad (1)$$

Yleinen vaihetekijä $e^{i\gamma}$ kumoutuu kompleksikonjugaattinsa kanssa mittauksessa $\left\langle\psi\middle|{e^{-i\gamma}M}^\dagger M\ e^{i\gamma}\middle|\psi\right\rangle=\left\langle\psi\middle|\ M^\dagger M\middle|\psi\right\rangle$, jolloin kubitille riittää kirjoittaa

$\left.\ |\psi\right\rangle=\cos{\frac{\theta}{2}\left.\ |0\right\rangle}+e^{i\varphi}\sin{\frac{\theta}{2}\left.\ |1\right\rangle}  \qquad \qquad \qquad \qquad \qquad   (2)$                                

Blochin pallo –simulaatiossa [1] havaitaan, että operoimalla tilaan $\left.\ 1|0\right\rangle+\left.\ 0|1\right\rangle$ Paulin matriisilla $Y=\binom{1\quad-1}{i\quad0}$ ja perään Hadamard-matriisilla $H=\frac{1}{\sqrt{2}}\binom{1\quad1}{1\quad-1}$ (tai päinvastoin) kompleksivektorin kärki kääntyy kompleksitasoon, jolloin siihen voidaan soveltaa vaihekulmaa φ muuttavia matriiseja S ja T. S saa aikaan 90 asteen kierron ja T 45 asteen kierron. Yleinen kubitin vaihetta siirtävä matriisi $P=\binom{1\quad0}{0\quad e^{i\varphi}}$.

Simulaatiossa yhteen kubittiin operoivat matriisioperaatiot voidaan tarkistaa laskemalla vastaavat matriisitulot. Todetaan, että kaikki edellä mainitut matriisioperaatiot ovat palautuvia, jolloin niitä vastaavat matriisit ovat unitaarisia ts. $M^\dagger M=1$, ja lasketaan malliksi yksi (Paulin Y matriisin transponointi ja kompleksikonjugointi kumoavat toisensa eli $Y^\dagger=Y$):

$$Y^\dagger Y=\binom{0\quad-i}{i\quad 0} \binom{0\quad-i}{i\quad 0} = \binom{1\quad0}{0\quad 1} \qquad \qquad \qquad \qquad \qquad      (3)$$

Kubitin mittaus tuottaa satunnaislukuja

Tarkastellaan kubitin puhdasta superpositiotilaa $\left.\ 1|0\right\rangle+\left.\ 0|1\right\rangle$. Tehdään siihen Hadamard-muunnos, jolloin saadaan tila $\left.\ 0.71|0\right\rangle+\left.\ 0.71|1\right\rangle$. Hadamard-muunnos merkitsee vektorin kiertoa xz-tasossa 45 asteen kulmaan ajateltavan akselin ympäri. Tilan $\left.\ 0|0\right\rangle+\left.\ 1|1\right\rangle$ muunnettu tila on $\left.\ 0.71|0\right\rangle-\left.\ 0.71|1\right\rangle$. Nämä tilavektorit muodostavat uuden ortogonaalisen kannan, jota merkitään $\left.\ |+\right\rangle,\ \left.\ |-\right\rangle$. Huomataan, että Blochin pallossa ortogonaaliset kantavektorit osoittavat vastakkaisiin suuntiin.

Jos nyt Hadamard-operaation jälkeen jatketaan tarkastelua ”laskennallisessa kannassa” $\left.\ |0\right\rangle,\ \left.\ |1\right\rangle$, huomataan, että operaatio tuottaa superpositiotilan, jossa kantavektorien amplitudit ovat yhtä suuret (amplitudit ovat kumpikin suuruudeltaan $1/\sqrt2$). Mittauksessa tällaisella tilalla on yhtä suuri todennäköisyys romahtaa tilaan $\left.\ |0\right\rangle$ ja tilaan $\left.\ |1\right\rangle$. Tehdään mittaus myQLM simulaatioympäristössä, joka on kevyt open access -versio QLM:stä [2].

prog.apply (H, qbits[0])
circuit = prog.to_circ()
%qatdisplay circuit //tuottaa kuvan q0

job1 = circuit.to_job()
job2 = circuit.to_job(nbshots = 5) //mittausta toistetaan viisi kertaa
job3 = circuit.to_job(nbshots = 42) //mittausta toistetaan 42 kertaa
result# = qpu.submit(job#)
Tuloksia:
(result1)
   state: |0⟩ probability amplitude: 0.7071067811865475+0j probability: 0.4999999999999999
   state: |1⟩ probability amplitude: 0.7071067811865475+0j probability: 0.4999999999999999
(result2)
   state: |0⟩ probability 0.6
   state: |1⟩ probability 0.4
(result3)
   state: |0⟩ probability 0.4523809523809524
   state: |1⟩ probability 0.5476190476190477

Kahden kubitin operaatiot, lomitukset ja mitä niillä saavutetaan

Siinä, missä He-atomin 1. virittyneessä tilassa elektronien lomittuminen tuottaa neljä tilaa (spinien vaihdon suhteen antisymmetrisen singlettitilan ja kolminkertaisen spinsymmetrisen triplettitilan), kubittien maksimaalinen lomittaminen tuottaa niin ikään neljä superpositiotilaa (nk. Bellin tilat):

$$\left.\ |\mathrm{\Phi}^+\right\rangle=\left.\ |B_{00}\right\rangle=\left.\ |00\right\rangle+\left.\ |11\right\rangle  \qquad \qquad \qquad \qquad \qquad  (4)$$

$$\left.\ |\mathrm{\Psi}^+\right\rangle=\left.\ |B_{01}\right\rangle=\left.\ |01\right\rangle+\left.\ |10\right\rangle    \qquad \qquad \qquad \qquad \qquad   (5)$$

$$\left.\ \left.\ |\mathrm{\Phi}^-\right\rangle=|B_{10}\right\rangle=\left.\ |00\right\rangle-\left.\ |11\right\rangle    \qquad \qquad \qquad \qquad \qquad    (6)$$

$$\left.\ |\mathrm{\Psi}^-\right\rangle=\left.\ |B_{11}\right\rangle=\left.\ |01\right\rangle-\left.\ |10\right\rangle     \qquad \qquad \qquad \qquad \qquad    (7)$$

Lomittunut tila on sellainen, jota ei voida esittää kahden hiukkasen tilojen tensoritulona. Jos yhtälössä (4) ensimmäinen kubitti mitataan ja tulos on 0, toisenkin kubitin arvo on 0 ja vastaavasti, jos ensimmäisen on 1, niin myös toisen on 1. Sanotaan, että (4) ja (6) ovat samansuuntaiset superpositiot siinä missä (5) ja (7) ovat vastakkaiset.

Lomittunut tila ei siis ole separoituva niin kuin tila

ensimmäisen kubitin mittaus, jos antaa tulokseksi 0, tuottaa uuden superposition

$$\left.\ |0\right\rangle\otimes\frac{1}{\sqrt2}\left.\ (|0\right\rangle+\left.\ |1\right\rangle)=\frac{1}{\sqrt2}(\left.\ |00\right\rangle+\left.\ |01\right\rangle). \qquad \qquad \qquad \qquad \qquad   (9)$$

Lomittuneita hiukkaspareja syntyy luonnossa esimerkiksi parinsyntyreaktioissa, mutta tässä kirjoituksessa tarkastellaan vain keinotekoisesti luotuja kubitteja (esimerkiksi suprajohtavia virtasilmukoita) ja niiden lomittamista. Lomittumista hyödynnetään kvanttilaskennan kontekstissa esim. kvanttiteleportaatiossa (QT), josta on jo useita kokeellisia verifikaatioita. QT ei ylitä valonnopeutta; sen nopeutta rajoittaa tarvittava klassinen viestikanava. Sen avulla kvantti-informaatiota voidaan kuitenkin siirtää luotettavammin kuin kokonaan klassisilla välineillä. Siirrettävät kubitit siirtyvät salattuna, eikä niitä voida teoriassakaan kopioida (kloonaamattomuusteoreema). Tarvittavat lomittuneet kubittiparit voidaan jakaa etukäteen, mutta niitä myös kuluu tiedonsiirrossa. Tarkastellaan kubittien lomittamista matriisien avulla ja käytän QT:ta esimerkkinä siitä, miten ja mihin kahden kubitin loogisia operaatioita käytetään.

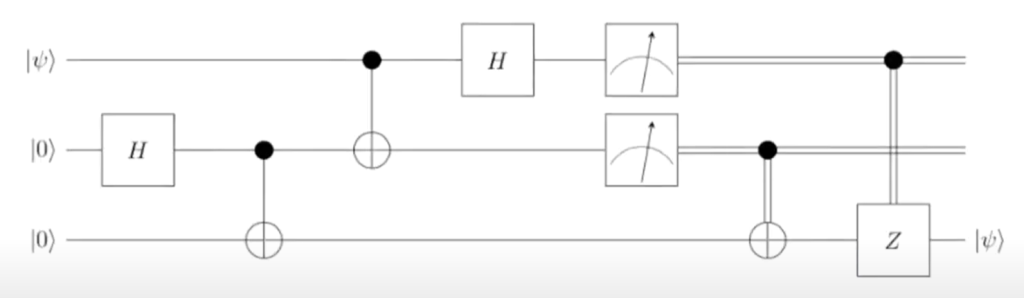
Käydään kaavio läpi vasemmalta oikealle. Hadamard-operaatio kahteen kubittiin ja sen perään CNOT-operaatio (controlled not = piirroksessa mustan pisteen ja rengastetun plusmerkin yhdistelmä) tuottaa Bellin $\left.\ |\mathrm{\Phi}^+\right\rangle$ tilan.

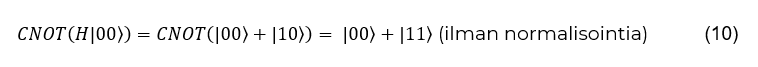
Seuraavaksi viestikubitti $\left.\ |\psi\right\rangle$ lomitetaan parin $\left.\ |\mathrm{\Phi}^+\right\rangle$ kanssa ja saadaan kolmen kubitin tila:

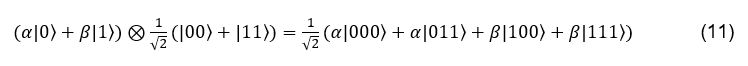
Seuraava CNOT muokkaa kolmen kubitin tilaa ja saadaan:

$$\ \ (11)\rightarrow\ \frac{1}{\sqrt2}\left(\alpha\left.\ |000\right\rangle+\left.\ \alpha|011\right\rangle+\left.\ \beta|101\right\rangle+\left.\ \beta|110\right\rangle\right)   \qquad   (12)$$

Seuraavaksi kolmen kubitin tilaan tehdään yksinkertainen Hadamard-muunnos, joka laajentaa superposition:

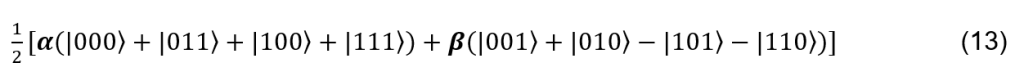
Seuraavaksi Alice mittaa molemmat kubittinsa ja valmistaa klassisen viestin Bobille. Jaetaan (13) kahdelle riville ja taulukoidaan mahdolliset tulokset kahden kubitin mittauksen jälkeen:

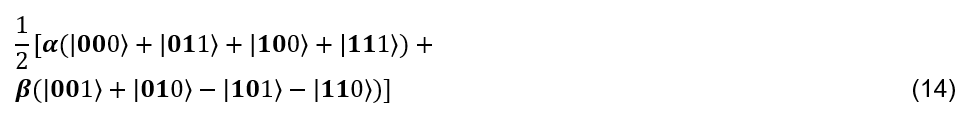
Taulukko 1. Klassisen kanavan sisältö/kubitti kvanttiteleportaatiossa.

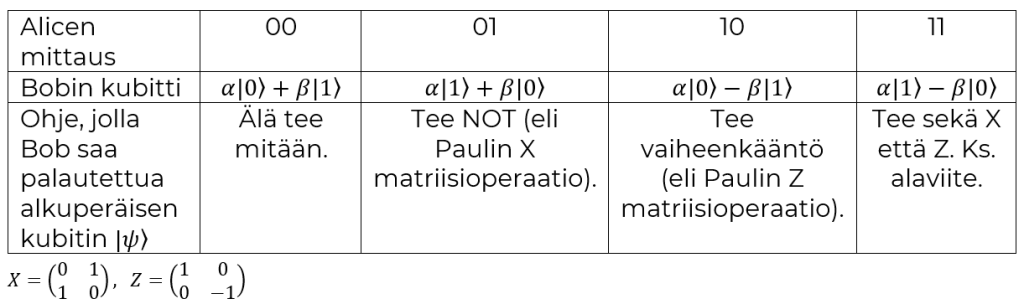
Kvanttilaskennan edellytykset ja monen kubitin laskenta

DiVincenzo listaa viisi edellytystä kvanttilaskennalle ja siihen päälle kaksi, jotta laskennasta päästään tietotekniikkaan (kvantti-ICT) [3]. Jottei tämä listaus jää vain teoreettiseksi, käydään samalla läpi IBM:n Yorktown-nimistä viiden kubitin kvanttitietokoneen realisaatiota.

1. Skaalattava kubittisysteemi.
2. Kubitit on voitava alustaa (esim. tilaan $\left.\ |00\ldots0\right\rangle$).
3. Laskenta-aikaa pidempi koherenttiaika (= aika, jonka jälkeen dekoherenssi pilaa laskennan).
4. Universaali joukko kvanttiloogisia operaatioita/portteja.
5. Yksittäinen kubitti on voitava mitata.
6. Paikallaan pysyviä ja liikkuvia loogisia kubitteja on voitava vaihtaa toisikseen.
7. Liikkuva kubitti on saatava laadukkaasti perille.

Ensimmäinen edellytys sisältää useita piirteitä. Yhden ja kahden kubitin systeemejä ei oikeastaan voida vielä laskea kvanttitietokoneeksi (vaikka muut edellytykset täyttyisivät). Kubitilla tarkoitetaan keinotekoista kvanttimekaanista hiukkasta, jonka Blochin pallon navalle alustettu tila voidaan kannanvaihto-operaatiolla muokata laskennalliseksi superpositioksi. Lisäksi kahden kubitin tiloja on voitava lomittaa. Lomittamalla kubitit niiden välille saadaan yhteys; all-to-all yhteyksiä ei vaadita. SWAP- ja MOVE-operaatioilla loogista kubittia, ts. kubitin tilaa voidaan liikuttaa kubittiarkkitehtuurissa.

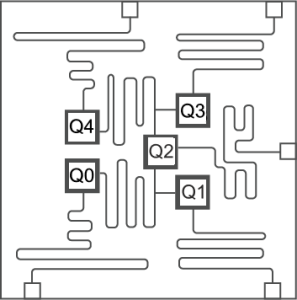
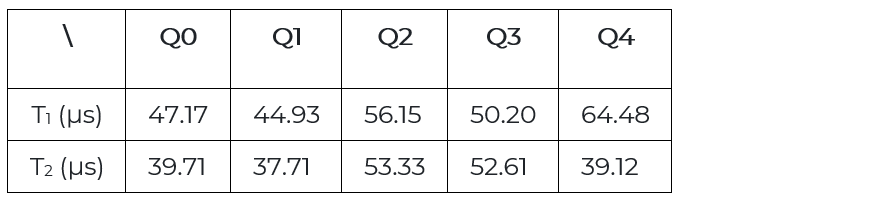
Kuvan laidoilla näkyvät ruudut ovat viiteen kubittiin liittyvät mikroaaltoresonaattorit, joilla kunkin kubitin tilaan voidaan operoida yksilöllisesti. Kubittien välissä näkyvät sillat mahdollistavat kubittien lomitukset. Kubiteille annetaan (T₁) relaksaatio- ja (T₂) koherenssiaikojen pituudet seuraavasti. Samalla datalehdellä todetaan, että gate-ajat yhden ja kahden kubitin operaatioille ovat luokkaa 83 ns ja 150-240 ns, tässä järjestyksessä.

Taulukko 2. Yorktown T₁– ja T₂-ajat

DiVincenzon listan kohdasta 4 voidaan todeta, että universaali joukko kvanttiloogisia operaatioita on esimerkiksi CNOT, H, X, Z ja $R(\frac{\pi}{8})$ (Solovayn – Kitaevin teoreema) [3].

Listan kohdat 6-7 ovat puolestaan melko käytännönläheisiä ja liittyvät siihen, että kvantti-ict:ssä ”liikkuvat kubitit” tai niiden realisaatiot ovat tavallisesti fotoneja joiden polarisaatiotilaa tai spatiaalista tilaa hyödynnetään. Niiden kanssa on haastavaa kommunikoida.

Johdannossa lupasin vielä lähestyä monen kubitin laskentaa, jonka toteuttaminen vaatii isompia kvanttikoneita kuin edellä kuvattu viiden kubitin realisaatio. Tarkastellaan aluksi laskennan vaativuusteoriaa (tai kompleksisuusteoriaa) ja sen tunnettua P = NP? ongelmaa, joka on yksi seitsemästä Clay Mathematics Instituten listaamasta miljoonan dollarin avoimesta ongelmasta vuodelta 2000.

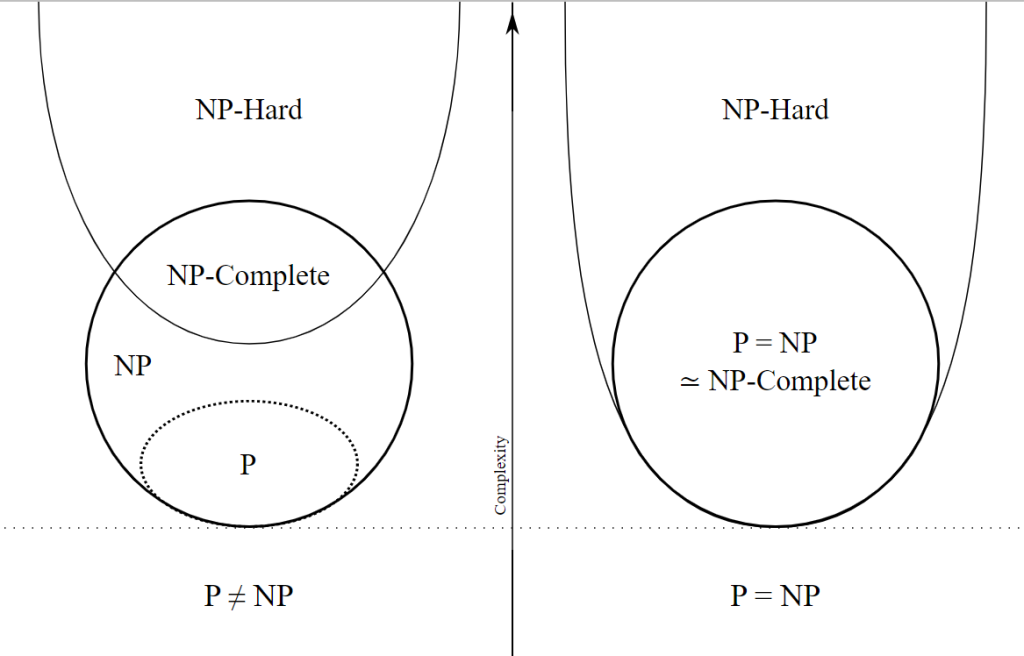
NP-täydellisiksi kutsutaan ongelmia, jotka ovat joko kaikki vaikeita eivätkä ratkea (P ≠ NP) polynomisessa ajassa (deterministisellä sekvenssikoneella) tai ovat kaikki helppoja ja ratkeavat (P = NP). Joukkoon P kuuluva ongelma voidaan ratkaista polynomisessa ajassa siinä missä joukon NP ongelman ratkaisu voidaan verifioida polynomisessa ajassa. Jokainen Sudoku-ruudukkoa (useammin kuin kerran) täyttävä huomaa, että ratkaisun verifioiminen on helpompaa kuin sen löytäminen. Jotta P olisi NP tarvittaisiin tehokas klassinen algoritmi, jolla NP-ongelman ratkaisun löytäminen olisi yhtä nopeaa kuin sen verifiointi ja vertautuisi laskenta-askelten lukumäärään N, joka on inputin latauksen vaatiman ajan polynominen (eikä eksponentiaalinen) funktio. Kvanttitietokone ei poista P = NP? ongelmaa, koska kvanttitietokone ei mahdu deterministisen sekvenssikoneen määritelmään. Propabilistiselle laskennalle onkin luotu uudet vaativuusluokat BPP (klassiselle) ja BQP (kvanttilaskennalle) ja ongelma P = PSPACE? (jonka osajoukko BQP on). Vaikkei näihin avoimiin kysymyksiin saataisi vastauksia lähitulevaisuudessa, kvanttitietokoneella voidaan silti saavuttaa monia etuja klassiseen laskentaan verrattuna. Esimerkiksi Shorin algoritmilla voidaan pienentää suurten lukujen tekijöihinjaon vaatimaa eksponentiaalista laskenta-aikaa, ts. pienentää eksponenttia. Yleistajuisessa kirjoituksessani käyn kursorisesti läpi yhden monen kubitin laskenta-algoritmin, Groverin algoritmin, joka pienentää strukturoimattoman tietokantahaun vaatimaa polynomista laskenta-aikaa O(N), lue ordo N, kvadraattisesti eli antaa tuloksen ajassa O($\sqrt N$).

Viittaan tässä IBM Quantum Composeriin [5], jonka dokumentaatiossa Groverin kvanttihakualgoritmi kuvataan yksityiskohtaisesti. ”Sävellystyökalulla” kvanttilooginen piiri voidaan kirjoittaa ”nuottiviivastoksi” ja se voidaan myös ajaa kvanttitietokonesimulaatiossa (sivustolta löytyy joitakin valmiita esimerkkejä). Sivustolla on esimerkiksi mahdollista koodata 2×2 Sudokun klassiset rivejä ja sarakkeita koskevat säännöt palautuvaksi kvanttilaskennaksi, jolloin laskennassa on kolme rekisteriä: neljä kubittia muuttujille, toiset neljä säännöille ja yksi kubitti takaisinlaskennan (uncomputation) tulokselle (Kuva 5).

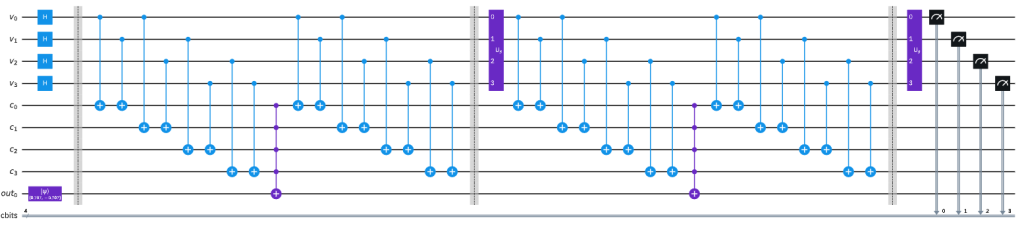
Kuvan 6 tulokset osoittavat selkeästi, että 2×2 Sudokun ratkaisut (16:sta alkeistapauksesta) ovat

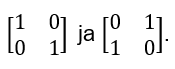
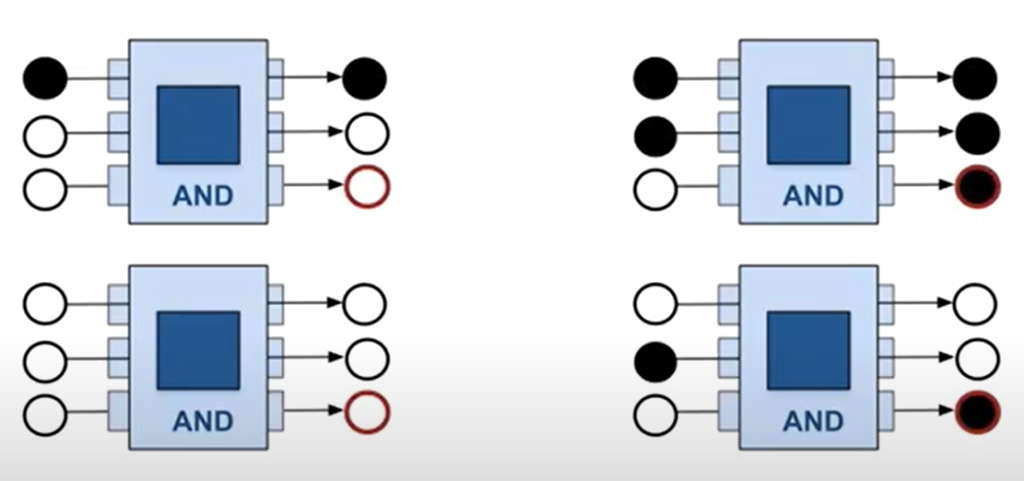
Laskennan stepit avataan viitteessä [5]. En toista niitä tässä vaan keskityn yhteen yksityiskohtaan, nimittäin siihen miten irreversiibeli klassinen looginen operaatio esimerkiksi AND (jonka outputista ei saa palautettua inputtia), voidaan muuttaa reversiibeliksi, jolloin se voidaan liittää osaksi kvanttiloogista algoritmia. Ensinnäkin outputteja on oltava yhtä monta kuin inputteja. Lisäksi kutakin inputtia kohti tulee olla yksikäsitteinen output (ja päinvastoin). Tämä tehdään käyttämällä apubittiä eli ancillaa. Kuvassa 7 tämä on tehty käyttäen kvanttiloogisia symboleja, jolloin bitit on korvattu kubiteilla. Oikealla keskimmäinen pallukka (2. kubitti) ilmaisee alkuperäisen (klassisen) outputin. Ylin pallukka ilmaisee 1. kubitin inputin (tulee suoraan läpi portista). Alimmainen pallukka on ancilla, joka tässä tapauksessa ilmaisee 2. kubitin inputin.

Viitteet

[1] Roope Salmi: Blochin pallo -simulaatio. https://bloch.ollpu.fi/

[2] Mikael Johansson (CSC – Tieteen tietotekniikan keskus) ja Jami Rönkkö (IQM Quantum Computers): Kvanttilaskentaa ja -ohjelmointia kahdessa tunnissa -webinaari. https://ssl.eventilla.com/event/jz2dA

[3] David P. DiVincenzo (IBM): The Physical Implementation of Quantum Computation. Quantum Physics, April 2000 https://arxiv.org/abs/quant-ph/0002077v3

[4] IBMQ – Yorktown device, https://github.com/Qiskit/ibmq-device-information/blob/master/backends/yorktown/V1/version_log.md

[5] IBM Quantum Composer v.3.9.87 https://quantum-computing.ibm.com/composer/docs/iqx/guide/grovers-algorithm