Lumiukko GeoGebralla – Walking in the Air
Vuosi sitten joulukuussa olin muutaman tunnin sijaisena 8 luokalla. Ryhmän opettaja pyysi minua ”koodaamaan” oppilaiden kanssa jotain kivaa GeoGebralla. Tämä lumiukkoprojekti onnistui suhteellisen mukavasti kahden 45 min oppitunnin aikana. Tein saman uudelleen lukion lyhyen matikan ryhmälläni ja myös suuri osa heistä sai aikaiseksi liikkuvan lumiukon. Jos oppilailla on perusosaamista GeoGebralla, niin tämä onnistunee vaikka 7-luokkalaisten kanssa, kunhan varaa riittävästi aikaa.
Tämä ohje toimii sekä GeoGebra 5, 6 ja GeoGebra 3D-versioilla. Kaikki komennot kirjoitetaan syöttökenttään. Tämän ohjeen teen GeoGebra 5.0.498 versiolla. Eri versioilla objektien automaattinen nimeäminen ei välttämättä toimi samalla tavalla.
Käynnistetään GeoGebra Classic 5. Näytä-valikosta kannattaa valita näkyville Algebra, 3D piirtoalue ja Syöttökenttä. Piirtoaluetta ei tarvita tässä vaiheessa. Koska lumiukossa on aika monta eri osata, niin myös laittaa Algebra-ikkunan yläreunan Järjestä-valikosta valinta kohtaan Objektin tyyppi. Näin osaset on helpompi hahmottaa.
Lumipallojen piirtämiseksi luodaan palloja. Haluan, että pallot ovat eri kokoisia ja suurimman säde on 2. Niinpä luon kolme pistettä 3D avaruuteen. Kokemus osoittaa, että rakennettaessa 3D objekteja, kannattaa käyttää koordinaatteja pisteiden luomisessa. Näin rakennelmiin on helpompi tehdä muutoksia jälkikäteen. Toisaalta myös luomisprosessin selittäminen kirjallisesti helpottuu. Opettajan kannalta saa myös mukavaa opetuskeskustelua, kun ensin piirtää joulupukin liitutaululle ja suunnittelee mittoja. Tätä luodessani käytin kultaista leikkausta ja sen likiarvoa, kun suunnittelin ukon muotoja.
A = (0, 0, 1)
B = (0, 0, 2.5)
C = (0, 0, 3.4)
Pallon saa luotua 3D-piirtoalueelle ikkunan pallotyökalujen avulla tai Pallo-komennolla. Luodaan alimmat pallot työkalujen avulla ja päällimmäisin komennolla.
Klikataan hiirellä Pallo-työkaluun, klikataan pisteeseen A ja vedetään pallon säde noin yhden mittaiseksi. GeoGebra luo pisteen nimeltä D ja pallon a.
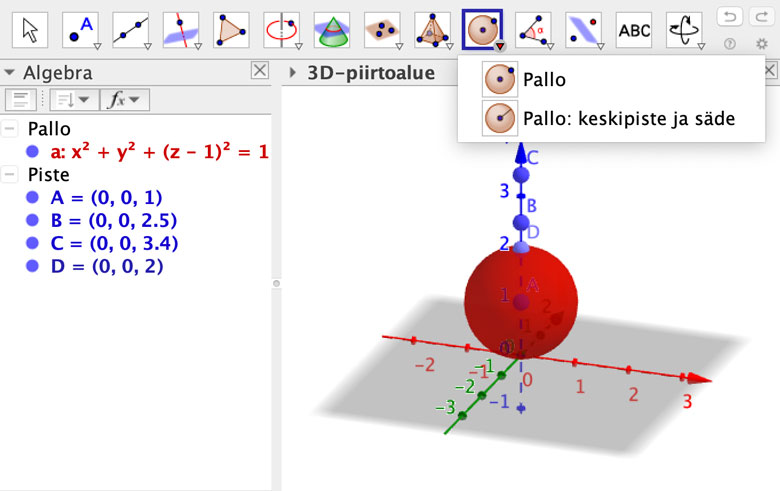
Luodaan seuraava lumipallo toisella työkalulla. Valitaan Pallo: keskipiste ja säde -työkalu, klikataan pisteeseen B ja määritetään säteeksi 0.618. GeoGebra luo pallon nimeltä b.
Kolmas pallo nimeltä c syntyy Pallo(Sphere)-komennolla
c = Pallo(C, 0.382)
Koristelin pallojen pintaa pistetyökalulla, näin sain silmät, nenän ja suun eli pisteet: E, … , N. Pisteiden sijoittamisen helpottamiseksi 3D-avaruutta voi liikuttaa xy-tasossa ja z-akselin suunnassa, kun painaa Vaihto-näppäimen pohjaan ja siirtää hiirellä avaruutta. Avaruuden pyörittäminen tapahtuu Kierrä 3D näkymää -työkalulla tai kun pitää ctrl-näppäintä pohjassa.
Hattu tehdään lieriötyökalulla, tehdään se silinterihatun näköiseksi. Luodaan piste O hatun alaosan keskipisteeksi ja P hatun lierin pisteeksi.
O = (0, 0, 3.6)
P = (0.5, 0, 3.6)
Lieri syntyy Ympyrä: keskipiste akselilla -työkalulla. Kun työkalu on valittu, klikataan ensin z-akseliin vaikkapa xy-tason alapuolella ja sen jälkeen pisteeseen P. Näin syntyy ympyrä d. Ympyrän olisi voinut luoda myös komennolla
d = Ympyrä(Suora(A,B), P)
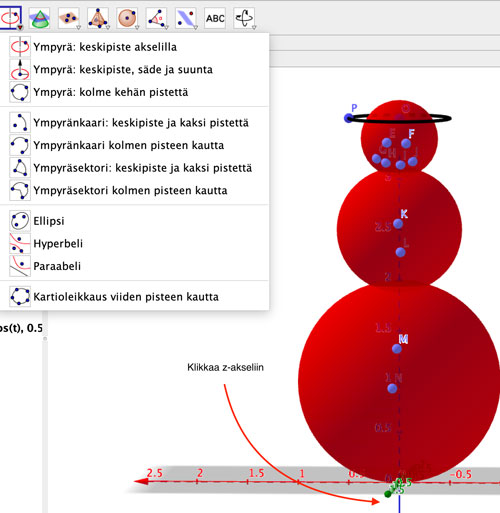
Hatun pääosaa varten luodaan lieriön korkein piste Q.
Q = (0, 0, 4.2)
Lieriö luodaan joko Lieriö-työkalulla kahden pisteen ja säteen avulla tai Lieriö(Cylinder)-komennolla
e = Lieriö(O, Q, 0.3)
GeoGebra luo lieriölle ympyrät e2 ja e3 sekä pinnan e4. On huomattava, että ympyröiden ja lieriöiden automaattinen nimeäminen on erilaista eri GeoGebran versioilla.
Nyt lumiukko on valmis ja viimeistään tässä vaiheessa se kannattaa tallentaa. Jos haluaa liikuttaa ukkoa, niin tässä vaiheessa ei vielä kannata muuttaa värejä. Tosin aloittelijat voivatkin lopettaa ukon värittämiseen.
Eri osien väritystä voi muuttaa valitsemalla objektit ja käyttämällä 3D-ikkunan työkaluja tai valitsemalla objektit Algebra-ikkunassa hiiren oikealla painikkeella ja Ominaisuudet kohdassa.
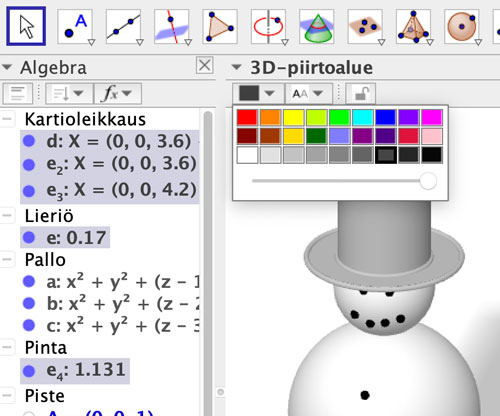
Kun mikään objekti ei ole valittuna 3D-piirtoalueella, niin koordinaattiakselit ja xy-tason saa pois näkyvistä yläreunan valikosta. Samassa kohtaa näkyy myös koti-ikoni. Se muuttaa 3D-näkymän oletuskohtaan. Objektien näkyvyyden saa helpoimmin pois Algebra-ikkunan pompuloista.

Liikkeen tuottamiseksi tarvitaan listoja. Yksittäisen liikkuvan listan jäseniä voi myös värittää. Niinpä luodaan kolme listaa hattu, pisteet ja pallot.
hattu = {d, g, h, e, i}
pisteet = {E, F, G, H, I, J, K, L, M, N, O}
pallot = {a, b, c}
Yksinkertaisin tapa liikuttaa listojen objekteja on käyttää apuna liukua ja Siirto(Translate)- komentoa. Sen ensimmäisenä syötteenä voi olla lista ja toisena paikkavektori tai piste. Mikäli syötteenä on piste, niin GeoGebra luo sen tilalle origosta lähtevän vektorin. Eli tässä tapauksessa vektorin Vektori(PP).
Luodaan piste PP ja liuku t.
PP = (5, 5, 5)
t = 5
Klikataan t-muuttujaa Algebra-ikkunassa hiiren oikealla painikkeella ja valitaan Ominaisuudet. Perusominaisuudet välilehteen laitetaan ruksi kohtaan Animaatio ja Liukusäädin välilehteen: Min = 0, Max = 1. Kannattaa itse kokeilla eri arvoja Animaatioaskeleelle ja Nopeudelle. Liuku t näkyy vain Piirtoalueella, niinpä valitaan se Näytä-valikosta. Ikkunoita voi siirrellä eri kohtiin vetämällä niitä eri ikkunoiden yläreunasta.
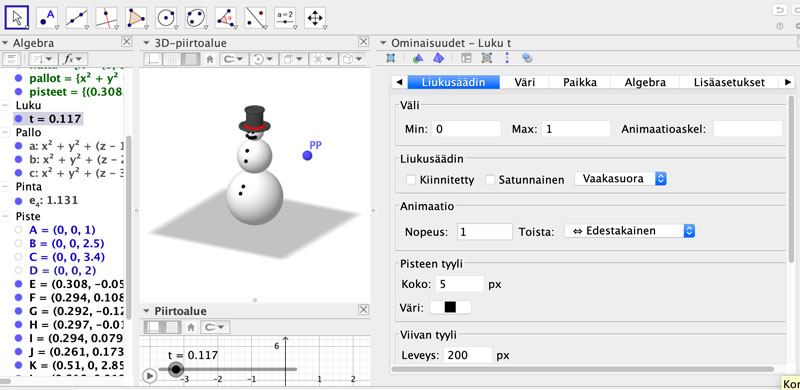
Kun syöttökenttään kirjoitetaan komento
Siirto(hattu, t*PP)
luo GeoGebra uuden listan nimeltä hattu’. Mikäli animaatio on päällä, niin näkyy, että vihreä hattu liikkuu vektorin $ 5\overline{i}+5\overline{j}+5\overline{k} $ suuntaisesti. Samalla tavoin saadaan muut osat liikkumaan.
Siirto(pisteet, t*PP)
Siirto(pallot, t*PP)
Liikkuvien listojen objekteja voi nyt värittää. Pysäytetään animaatio Piirtoalueen t-liu’usta tai hiiren oikealla painikkeella Algebra-ikkunassa, kun t-liuku on valittuna. Valitaan ensin kaikki alkuperäisen objektit valitsemalla hiirellä ensin jokin objekti Algebra-ikkunassa ja sen jälkeen painetaan ctrl-A (Macissä cmd-A) tai Muokkaa valikosta Valitse kaikki. Hiiren oikealla painikkeella valitaan Näytä objekti pois päältä. Tämän voi joutua tekemään kaksi kertaa, mikäli osa objekteista ei alun perin ole näkyvissä. Muutetaan listat hattu’, pallot’ ja pisteet’ näkyviksi Algebra-ikkunan pompulan tai hiiren oikean painikkeen avulla. Kun lista hattu’ on valittuna sen kaikki osat saa väritettyä kerralla. Tässä vaiheessa voi alkaa hyräilemään Lumiukko-animaatioelokuvasta tuttua laulua ”Walking in the Air”, samalla kun laittaa animaation päälle.
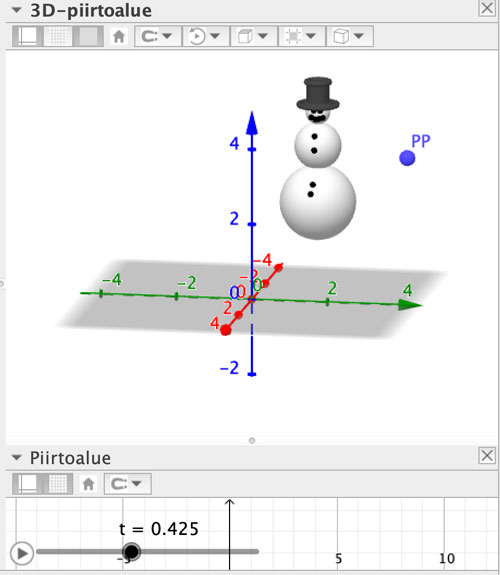
Ukkoa kuljettaminen pitkin avaruuden käyrää pitkin tapahtuu seuraavasti. Luodaan ensin parametrinen käyrä, tässä tapauksessa ruuvikäyrä käyttäen apuna t -liukua.
PP = (cos(t) – 1, sin(t), 0.1*t)
Liu’un t ominaisuuksissa kannattaa muuttaa maksimiarvo suuremmaksi, vaikkapa arvoksi 2 π.
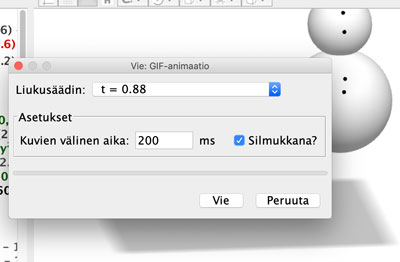
Gif-animaatio saadaan tallennettua 3D-piirtoalueelta seuraavasti. Sulje Piirtoalue ja valitse mielekkäät arvot t-liu’ulle. Animaatioaskelta ei kannata laittaa liian pieneksi, ettei tule järjettömän isoja tiedostoja. Valitaan t-liun animaatio päälle hiiren oikealla painikkeella ja säädetään 3D-piirtoalueen koko sopivaksi. Valitaan Tiedosto-valikosta Vie → Vie: Piirtoalue Gif animaationa… Liukusäädin valitaan t:ksi ja Kuvien välinen aika sopivaksi. 200 ms tarkoittaa viittä kuvaa sekunnissa.
Tässä tarinassa esitetty GeoGebra-tiedosto löytyy GeoGebra materiaaleista osoitteessa

Lisää luettavaa
Korhonen, Luoma-aho, Rahikka. Geogebra -opas. MFKA 2012.
Mikon fysiikan ja matikan blogi https://mikonfysiikka.wordpress.com/
Rahikka. Listat GeoGebrassa. Dimensio 6/2018.







