Kolme tehtäväkokoelmaa
Matematiikkamateriaalia on paljon monella kielellä. Suomenkielisiä matematiikan tehtäväkokoelmia ei ole kuitenkaan verkossa vapaasti saatavissa montakaan, vaikka tehtäviä sinänsä on paljon hajallaan monilla sivustoilla. Esittelen seuraavassa kolme kokoelmaa. Niiden tehtäviä opettaja voi käyttää oppilaidensa kanssa, oppilas itsenäisessä opiskelussa ja muukin matematiikan harrastaja oman mielensä harjaannuttamisessa ja virkistämisessä.
Ensimmäinen on Iso M -tehtäväkokoelma [1]. Se on ollut verkossa jo pitkään, mutta ajankohtainen se on siksi, että MatTa-sivusto [2] on revisioitu – korjattu/tarkistettu/ajanmukaistettu – syksyn 2023 aikana. Alun perin tehtäväkokoelma on koottu lukiotasoisen matematiikan kertaamiseen Teknillisen korkeakoulun matematiikan laitoksella jo edellisen vuosituhannen puolella alkaneen Matematiikkaa tietokoneavusteisesti (MatTa) ‑projektin [3] yhteydessä.
Kokoelmassa on kuutisenkymmentä tehtävää. Ne on ryhmitelty sekä aihepiireittäin että alkuperänsä mukaisesti. Valtaosa on valikoituja ylioppilaskirjoitustehtäviä ja TKK:n pääsykoetehtäviä. Esimerkkeinä voivat olla seuraavat kolme:
Näkökulmia (aihepiiri Avaruus): Kuu näkyy Maasta 0,52 asteen kulmassa. Kuun säde on 1740 km ja Maan säde on 6370 km. Missä kulmassa Maa näkyy Kuusta?
Helsingistä napapiirille (aihepiiri Maantiede): a) Kuinka monta kilometriä maan pintaa pitkin laskettuna on yksi leveysaste? b) Kuinka pitkä matka on linnuntietä Helsingistä pohjoiselle napapiirille? Maapallon säde on 6370 km. Tarvittavat maantieteelliset leveydet ovat: Helsinki 60o pohjoista leveyttä, napapiiri 66,5o pohjoista leveyttä.
Elämän sileät särmät (arkkitehtiosastojen valintakoetehtävä vuodelta 1993): ”Elämän sileät särmät”-patsas on kuution muotoinen pronssiveistos, jonka särmän pituus on 3,2 m. Lisäksi patsas on ontto siten, että sen kaikki sivutahkot ovat yhtä paksut. Mikä on sivutahkojen paksuus, kun patsaan ontto osa on 95
Toinen kokoelma on Solmun tehtäviä [4]. Se piilee vaatimattomasti matematiikkalehti Solmun verkkosivulla ”Matematiikan opetus” otsikon ”Tehtäviä” alla. Aihepiirit ovat monipuolisia ja tehtävät monen tasoisia. Esimerkiksi keskimmäisen seuraavista arvioidaan sopivan ”lukiolaisten lisäksi myös edistyneille yläkoululaisille”:
Montako alkiota on suurimmassa joukon A = {1, 2, . . . , 547} sellaisessa osajoukossa, jossa minkään kahden luvun summa ei ole jaollinen 42:lla? (Solmu 1/2002: Solmun tehtävät, tehtävä 5)
Opri kirjoitti 2022 luvun listan seuraavasti: Listan kolmas luku on toinen luku jaettuna ensimmäisellä luvulla, listan neljäs luku on kolmas luku jaettuna toisella luvulla, ja niin edelleen, esimerkiksi listan 100. luku on 99. luku jaettuna 98. luvulla. Mikä on Oprin listan viimeinen luku, jos sen ensimmäinen luku on 20 ja toinen luku on 22? (Solmu 3/2022 s. 29)
Linnuston suojeluarvoa laskettaessa otetaan huomioon lajin uusiutumiskyvyn indeksi (U), joka lasketaan linnun painosta, lajin lisääntyvän kannan suuruus Suomessa (K) ja lajin uhanalaisuuden indeksi Suomessa (S). Lajikohtainen suojelupistearvo (SA) lasketaan kaavalla $\frac{U\cdot S}{K}$. Pistearvo on sitä korkeampi, mitä hitaampi laji on lisääntymään, mitä uhanalaisempi se on ja mitä pienempi on kannan koko Suomessa. Tietyn elinympäristön suojeluarvo (LA) saadaan kertomalla kunkin alueella pesivän lajin muunnettu parimäärä (M), joka on parimäärä potenssiin 0,7, kyseisen lajin suojeluarvolla (SA) ja laskemalla saadut luvut yhteen, siis kaava on $\sum_{}^{}(SA\cdot M)$ (Ote pitemmästä tekstistä [5].)
Kolmas kokoelma voisi olla MAOLin matematiikan tehtävät. Sellaista kokoelmaa ei toistaiseksi ole verkossa, vaikka hyvin voisi olla, sillä niin paljon tehtäviä on tuotettu ja julkaistu vuosien aikana, sekä verkkosivujen materiaalipankissa että muualla. Kirjojakin on useita, esimerkiksi Matematiikan pulmasivut (Heinonen, Martti, 2018) ja Lisäpotku (peruskoulukilpailutehtäviä, Korhonen, Hannu ja Latva, Heimo, 2000) sekä pari muuta kilpailumatematiikan tehtäväkokoelmaa.
Heinosen kirjassa on hänen itse laatimansa Dimensiossa julkaistut pulmasivut vuosilta 2006–2019 ja nelisenkymmentä julkaisematonta sivua, yhteensä lähes 300 tehtävää. Muiden tekemiä pulmasivuja Heinonen ei kirjaansa ottanut.
Muiden kuin Heinosen tekemiä pulmasivuja on ilmestynyt sekä paperilehdessä että sähköisessä [6] ehkä yhtä paljon kuin Heinosen tekemiä, esimerkiksi:
Mehiläisten määrä mehiläisperheessä on aina viisinumeroinen luku. Mehiläisperhe juhlii onnellista hetkeä aina, kun mehiläismäärä on palindromiluku. Kesän alussa perheessä on 10 000 jäsentä. Joka päivä kuningatar munii noin 1 000 munaa. Kuinka monta onnellista hetkeä mehiläisperheessä on kesän aikana? (Toukokuun pulmat 16.5.2023)
Vuosiluvuissa 2000–2023 on kolme alkulukua. Mitkä ne ovat? (Joulukuun pulmat 4: Vuosilukuja, 27.12.2022, tehtävä 1)
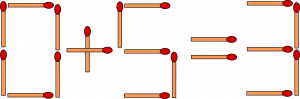
Siirrä yhtä tikkua niin, että yhtälö on tosi. Ongelmalle löytyy kaksi ratkaisua. Etsi ne molemmat. (Maaliskuun pulmasivut: Tikusta asiaa 15.3.2022, tehtävä 1)
Jotkut pulmasivuista ovat yhteen aihepiiriin liittyviä tehtäväkenttiä, usein vaikeutuvia sarjoja, eivätkä irrallisia pikkutehtäviä, esimerkiksi Fibonacci-kello [7] ja Ratsun reitti [8].
Viime vuosien pulmasivujen esittäminen yhtenäisenä kokoelmana ei vaatisi olennaista lisätyötä, sillä ne ovat jo nyt julkisesti saatavissa [9]. Käyttöä kyllä tehostaisi niiden kerääminen yhteen ja jonkinlainen luokittelu aihepiirin tai vaikeustason mukaan.
MAOLin tehtäväkokoelmaa ei kannattaisi piilottaa jäsensivujen salasanojen taakse, vaan pitää se julkisena Dimensio-lehden tapaan. Se korostaisi MAOLin tehtävää matematiikan puolesta puhujana ja innostuksen herättäjänä. Vaikutusta tehostaisi se, että pulmasivujen tehtävät eivät ole ihan tavanomaista koulumatematiikkaa, vaan näyttäisivät matematiikasta sellaisia puolia, jotka eivät tule aina esille kouluopetuksessa. Sellaisina ne voisivat tarjota pohdiskeltavaa myös matematiikan harrastajille. Samaan kokoelmaan voisi sisällyttää jäsensivuilla olevia Survo-ristikoita ja topologian harrastustehtäviä sekä muuta vastaavaa materiaalia. Kokoelman koostaminen sopisi hyvin liiton juhlavuoden imagonnostattamisprojektiksi.
Päätoimittajan lisäys artikkeliin
MAOL-toimisto ja MAOLin viestintätoimikunta ovat linjanneet verkossa julkaistavan Dimension pulmasivujen ratkaisut MAOLin jäseneduksi. Itse tehtävät ovat kuitenkin julkisia. Yksittäinen opettaja voi tukea MAOL ry:tä kuulumalla MAOL ry:hyn, jotta MAOL voi yhä tulevaisuudessa innostaa matematiikan opettajia julkaisemalla pulmatehtäviä verkkolehdessään.
Lähteet
[1] Iso M-tehtäväkokoelma osoitteessa https://matta.math.aalto.fi/isomharj/tehttoc.html
[2] MatTa-sivusto osoitteessa https://matta.math.aalto.fi/
[3] Kivelä, Simo K. (2000): Matematiikan opiskelua digitaalisessa ympäristössä: Iso-M-projektin lähtökohdat, periaatteet ja toteutus. Teknillisen korkeakoulun matematiikan laitoksen raporttisarja C14.
[4] Solmu/Matematiikan opetus/Tehtäviä osoitteessa https://matematiikkalehtisolmu.fi/opetus.html#tehtavia
[5] Ekologisia tehtäviä osoitteessa https://matematiikkalehtisolmu.fi/2000/ekoteht/
[6] Dimension pulmasivuja https://staging.dimensiolehti.qs.fi/category/pulmasivut/
[7] Matematiikan pulmasivu: Fibonacci-kello. Dimensio 5/2016 s. 76.
[8] Huhtikuun pulmat 2023: Ratsun reitti. Dimensio 18.4.2023 https://staging.dimensiolehti.qs.fi/huhtikuun-pulmat-2023-ratsun-reitti/
[9] Dimension pulmasivu -kategorian lisäksi haku https://staging.dimensiolehti.qs.fi/page/5/?s=pulmasivu antaa myös muutamia fysiikan ja kemian pulmasivuja sekä joitakin artikkeleita, joissa on viitteitä pulmasivuihin ja tehtäviä, jotka eivät ole ilmestyneet pulmasivuilla.







