Kevään 2021 fysiikan ylioppilaskoe
Osanottajamäärä jatkoi kasvuaan
Kevään 2021 fysiikan ylioppilaskokeeseen ilmoittautui 9499 ja osallistui 8998 kokelasta. Osallistujamäärä on lisääntynyt jo useamman koekerran ajan. Tämä tarkoittaa, että yhä useampi lukiolainen opiskelee nykyään fysiikkaa enemmän kuin yhden pakollisen kurssin verran, mikä on hyvä asia.
Kaikkien kokelaiden pistemäärien keskiarvo kevään kokeessa oli 57,0 ja ensimmäistä kertaa fysiikan kokeeseen osallistuvien 55,7. Kuten tunnettua, arvosanojen pisterajat määräytyvät kokeeseen ensi kertaa osallistuvien kokelaiden suoritusten perusteella. Korkeakoulujen valintamenettelyjen muuttuminen ja vuonna 2019 voimaan tullut hyväksyttyjen ylioppilaskokeiden rajaton uusimismahdollisuus ovat lisänneet huomattavasti kokeiden uusijoiden määrää. Uusijoiden osuus tämän kevään fysiikan kirjoittajista oli noin 22
Yleisradion abitreenien kyselyssä kolmannes vastanneista kokelaista piti kevään 2021 fysiikan koetta juuri sopivana ja yli 40
Sensoroinnista käytiin keskustelua
Julkisuudessa on aika ajoin käyty keskustelua ylioppilaskokeiden sensoroinnista, niin myös kevään 2021 ylioppilaskokeiden yhteydessä. Esille otetuissa esimerkkitapauksissa on usein kyse siitä, että opettaja on alustavassa arvostelussaan antanut kokelaalle merkittävästi enemmän pisteitä kuin sensori varsinaisessa arvostelussa. Alustavan arvostelun ja sensoreiden arvostelun välisiä eroja seurataan sensoroinnin kuluessa, ja niitä havaitaan hieman useimmin juuri tähän suuntaan kuin päinvastaiseen suuntaan. Mikäli sensorin ja opettajan antamat pisteet tehtävästä poikkeavat huomattavan paljon toisistaan, myös toinen sensori tarkastaa tehtävän, joskus kolmaskin.
Erot alustavan ja varsinaisen arvostelun välillä ovat luonnollisia, sillä opettajat ja sensorit perustavat arvostelunsa ainakin osittain eri näkemyksiin siitä, mistä pisteitä annetaan ja mistä niitä otetaan pois. Sensoroinnin tärkein periaate on mahdollisimman yhtenäinen ja tasapuolinen arvostelu kaikkien kokelaiden kesken, ja tämä vaikuttaa siihen, millä tavoin ratkaisut pisteytetään arvostelussa. Myös fysiikan jaoksen tekemä sensoreiden työn laadun seuranta keskittyy arvostelun tasapuolisuuden varmistamiseen.
Huomioita tehtävistä ja ratkaisuista
Tehtävä 1 Monivalintatehtäviä fysiikan eri osa-alueilta (8898 vastaajaa)
Tehtävän viisi ensimmäistä kohtaa käsittelivät perusmekaniikkaa. Niissä tarkasteltiin leikkijunien liikettä ja törmäyksiä. Hankalimmaksi osoittautui kohta 5, jossa veturia vedettiin vakiovoimalla ja kysyttiin, mihin suureeseen veturin liike-energian muutos on verrannollinen. Vain 39
Kohdissa 5 ja 6 pidettiin varattua hiukkasta paikallaan homogeenisessa sähkökentässä ja magneettikentässä ja kysyttiin, miten hiukkanen alkaa liikkua, kun se päästetään irti. Vain vajaa kolmannes tiesi, että magneettikenttä ei kohdista paikallaan olevaan varattuun hiukkaseen voimaa eli että hiukkanen pysyy paikallaan.
Kohdassa 10 kysyttiin, miksi kasvihuonekaasut lämmittävät ilmakehää. Vain 5,8
Oikeiden vastauksen osuudet tehtävän 1 osakohdissa olivat: 1. 78,70
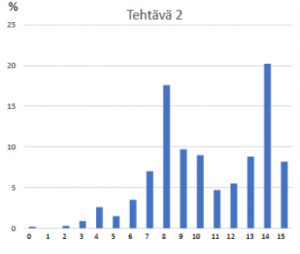
Tehtävä 2 Pikajuoksu (8700 vastaajaa)
Tässä tehtävässä oli annettu Carl Lewisin väliajat 100 metrin maailmanennätysjuoksussa Tokiossa vuonna 1991. Ensimmäisessä kohdassa piti esittää kuvaaja väliajoista matkan funktiona. Kuvaajalla tarkoitetaan mittauspisteitä sekä niihin tehtyä graafista tasoitusta eli mittauspisteisiin hyvin istuvaa käyrää. Mitattuja pisteitä vastaavaa funktiota ei löydy valmiina mistään, sillä liike on aluksi kiihtyvää ja lopussa Lewis etenee vakionopeudella. Tämän takia graafinen tasoitus on tässä tehtävässä paras ratkaisu kuvaamaan funktiota. Murtoviivaa tai mittauspisteisiin (osaan tai kaikkiin) sovitettua suora ei huolittu tasoitukseksi, mutta mm. kaikki astetta kaksi korkeammat polynomisovitukset päätettiin hyväksyä, jos ne sopivat riittävän hyvin mittauspisteisiin.
Kohdassa 2 tasoitusta piti hyödyntää interpolointiin eli piti määrittää Lewisin väliaika 75 metrin kohdalla. Vastauksen sai monenlaisella tasoituksella osumaan sensoreiden määrittelemään hyväksymisikkunaan.
Viimeisessä kohdassa piti soveltaa loppupään mittauspisteiin tasaisen liikkeen mallia, eli sovittaa niihin t(v)-suora, ja ekstrapoloida sen avulla Lewisin kuvitteellinen aika 200 metrin matkalla. Yleisin virhe oli suoran sovittaminen kaikkiin mittauspisteisiin. Yhtä lailla väärin oli laskea 200 metrin aika 100 metrin keskinopeuden avulla. Ratkaisun sai tehdä joko graafisesti tai laskennallisesti.
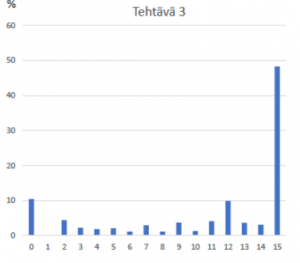
Tehtävä 3 Kaasupullo (6800 vastaajaa)
Tehtävässä piti määrittää argonilla täytetyn kaasupullon massa, kun pullon tilavuus, tyhjän pullon massa, kaasun paine ja kaasun lämpötila tiedettiin.
Suorin tapa ratkaista tehtävä oli olettaa argonin käyttäytyvän ideaalikaasun tavoin ja laskea ideaalikaasun tilanyhtälöstä argonin ainemäärä. Argonin moolimassa tunnetaan, joten argonin massa saadaan silloin laskettua.
Moolimassan sijasta kokelas saattoi käyttää ideaalikaasun moolitilavuutta ja argonin tiheyttä. Taulukoissa oli epäselvyyttä sen suhteen, vastaako niissä annettu arvo lämpötilaa 0 °C (oikein) vai 20 °C (väärin). Sensorit ottivat tämän huomioon hyväksymällä kumpaakin lämpötilan arvoa vastaavan tuloksen.
Osa kokelaista laski tehtävän ”vapauttamalla” argonin normaaliin ilmapaineeseen ja lämpötilaan 0 °C tai 20 °C ja määrittämällä kaasun tilavuuden näissä olosuhteissa yleisen kaasulain avulla. Tässäkin hyväksyttiin molemmat lämpötilan arvot.
Todetaan tässä, että eräs syy taulukkoarvojen sekavuuteen johtunee kaasun tilasta käytetystä lyhenteestä NTP. Kansainvälisissä lähteissä NTP (”normal temperature and pressure”) määritellään tilana, jossa lämpötila on T = 293,15 K (t = 20 °C) ja paine p = 101,325 kPa (1 atm). Suomessa normaalilämpötilaksi kutsutaan lämpötilaa T=273,15 K (t = 0 °C) ja normaalipaineeksi p=101,325 kPa (1 atm). Kaasun sanotaan olevan normaaliolosuhteissa, kun sillä ovat nämä lämpötilan ja paineen arvot. Normaaliolosuhteista käytetään Suomessa joskus lyhennettä NTP, mikä on ristiriidassa lyhenteen kansainvälisen käytön kanssa. Lyhenteen käyttöä olisi tämän takia parasta välttää ja puhua vain normaaliolosuhteista.
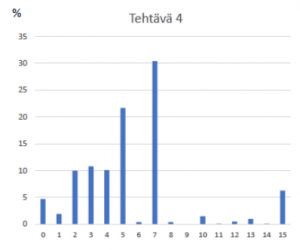
Tehtävä 4 Siltakytkentä (2713 vastaajaa)
Virtapiirit ja yleensäkään sähköopin tehtävät eivät ole viime aikoina nauttineet kaksista suosiota kokelaiden keskuudessa, eikä osaamisen taso ole vastanneidenkaan keskuudessa ollut aina kovin korkea. Tämä pätee myös tämänkertaiseen sähköopin tehtävään, jonka aiheena oli siltakytkennän käyttö tuntemattoman vastuksen resistanssin määrittämiseen. Tehtävän vaativuus kasvoi kohta kohdalta niin, että viimeiseen kohtaan esitti oikean ratkaisun vain 6
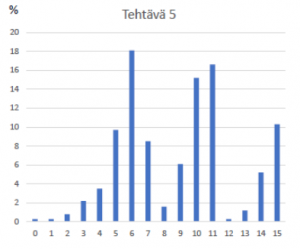
Tehtävä 5 Voimat (8353 vastaajaa)
Tehtävässä tarkasteltiin pyöräilijään ja polkupyörään sekä keinujaan keinukarusellissa vaikuttavia voimia. Kummassakin tapauksessa piti valita oikea annetuista vaihtoehdoista ja nimetä voimat. Koska etukäteisarvio oli, että oikean vaihtoehdon valinta voi tuottaa monille vaikeuksia, pisteitä annettiin kohtuullisen pistesaldon takaamiseksi oikein nimetyistä voimista, vaikka kuva olisikin valittu väärin.
Pyöräilijän tapauksessa eniten tehty väärä valinta oli se, jossa takapyörän lisäksi myös etupyörään vaikutti kulkusuuntaan osoittava lepokitka. Tehtävään valittiin kulkuvälineeksi polkupyörä, koska polkupyörän takavetoisuuden voi olettaa olevan kaikille kokelaille tuttua. Keinun tapauksessa yleisimmän väärän valinnan mukaan karusellissa istujaan vaikuttaa painon ja istuimen tukivoiman lisäksi radan keskustasta ulospäin suuntautuva voima – tuttuakin tutumpi ”keskipakovoima”.
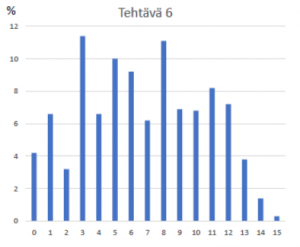
Tehtävä 6 Maanjäristysaallot (2623 vastaajaa)
Maanjäristysaallot innostivat kokelaita yllättävän vähän, jopa vähemmän kuin siltakytkentätehtävä. Ensimmäisen osion laskutehtävät vielä sujuivat, mutta monelle kokelaalle tuntui olevan jossain määrin vieras ajatus, että maanjäristyksen aiheuttamat paineaallot voivat edetä kiinteässä aineessa sekä pitkittäisinä että poikittaisina. Ja jos tämä oli kokelaalle tuttua, niin nesteistä tutun tiedon pitkittäisestä aaltoliikkeestä vain harva osasi yhdistää koskevan myös maapallon nestemäisessä osaa.
Arvostelussa päädyttiin hyväksymään laajasti kuvauksia aaltojen heijastumisesta ja taittumisesta maapallon eri kerrosten rajapinnoilla, ja näin tehtävästä sai pisteitä melko ylimalkaisillakin tiedoilla.
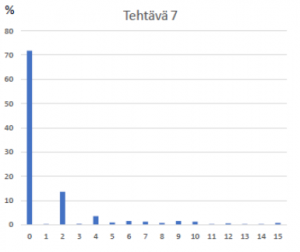
Tehtävä 7 Heijastuminen ohuesta kalvosta (1829 vastaajaa)
Heijastuminen ohuesta kalvosta on perinteinen valon interferenssiin liittyvä ilmiö, joka on varsinkin takavuosina ollut varsin usein ylioppilastehtävän aiheena. Tehtävä oli tämänkertaisen kokeen vähiten valittu tehtävä ja myös kaikkein huonoiten osattu.
Eräs kompastuskohta vaikutti olevan tehtävässä tarkasteltu tilanne, jossa valo osuu pintaan kohtisuorasti. Tavallisestihan valon heijastumista ja taittumista tarkastellaan vinosti tulevan valon tapauksessa. Tämän takia monissa vastauksissa eksyttiin tarkastelemaan kokonaisheijastumista, joka saattaisi selittää heijastuneen valon kirkastumisen tietyissä tilanteissa.
Koetta tarkastaessa saattoi panna merkille, että useimmissa kouluissa interferenssi ohuissa kalvoissa on ilmeisesti jäänyt vähälle huomiolle. Joukosta erottuivat ne koulut, joissa asia oli ollut esillä, sillä niissä yleensä useampi oppilas osoitti osaamista.
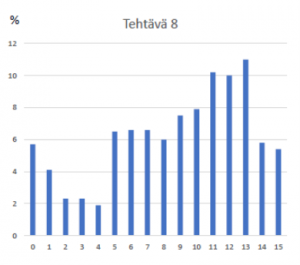
Tehtävä 8 Radon (4602 vastaajaa)
Radonin lähettämän ionisoivan säteilyn vaarallisuus terveydelle oli hyvin kokelaiden tiedossa, mutta se, mihin sen vaarallisuus huoneilmassa liittyy, tiedettiin huonommin. Vastauksesta piti ilmetä, että huoneilman radon päätyy hengitettäessä keuhkoihin, jossa sen säteily voi aiheuttaa vaurioita solujen perimäainekseen.
Tehtävän 2. kohdassa piti selvittää, kuinka monta α-hiukkasta ja kuinka monta β—-hiukkasta radonin tehtävässä annetussa hajoamisketjussa vapautuu. Tähän osattiin vastata hyvin, mutta jotkut olivat laskeneet myös beetahajoamisessa syntyvät antineutriinot beetahiukkasiksi.
Kohdassa 8.3 saattoi käyttää hyväkseen taulukkokirjassa olevaa aktiivisuuden kaavaa. Sensorit suhtautuvat yleensä penseästi pelkän kaavan kopiontiin taulukosta ilman, että kokelas jollakin tavalla osoittaa tietävänsä, miksi juuri kyseinen kaava liittyy tilanteeseen. Toimiva tapa on nimetä kaavassa käytettävät suureet ja liittää kaava niiden avulla tehtävän ratkaisuun. Tässä tapauksessa vaadittiin, että ainakin kaavassa oleva hajoamisvakio λ oli nimetty oikein eikä esimerkiksi kutsuttu sitä ”radonin aallonpituudeksi”.
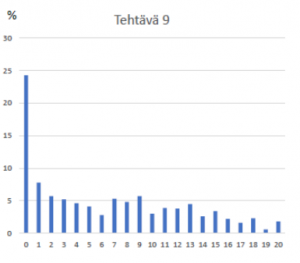
Tehtävä 9 Sauvan tasapaino (5317 vastaajaa)
Osan III ensimmäisessä tehtävässä tarkasteltiin vaakasuorassa asennossa olevaa sauvaa, jonka toinen pää nojaa vapaasti seinään ja toinen pää on tuettu narulla, joka on toisesta päästään kiinni seinässä. Osan III tehtävät ovat usein soveltavia ja tavallisesti aineistoihin pohjautuvia, mutta tällä kertaa yhtenä oli tällainen hieman vaativampi perusmekaniikan tehtävä.
Tehtävän 1. osassa piti saada selville, kuinka pieni sauvan ja kiinnitysnarun välisen kulman pitää vähintään olla, jotta sauva pysyy paikoillaan. Sen määrää lepokitkan suurin mahdollinen arvo – sen lepokitka tässä ääritapauksessa saavuttaa.
Kuten mekaniikan tehtävissä yleensäkin, tässäkin piti piirtää ensin voimakuvio. Lopullisessa Hyvän vastausten piirteistä käy ilmi, mitä sensorit voimakuviolta vaativat: ”Voimakuviosta ei saa pisteitä, jos yksikin voima puuttuu tai siinä on ylimääräisiä voimia tai jos voimia on jaettu komponentteihin, jotka eivät erotu voimista tai joiden pituudet eivät ole oikein. Voimakuvion pisteistä vähennetään yksi piste, jos voimat eivät ole kiinni kappaleessa tai vaikuttavat väärään pisteeseen tai jos voimien summa on selvästi nollasta poikkeava.” Muutamissa vastauksissa oli sauvan seinän puoleiseen päähän piirretty yläviistoon osoittava tukivoima. Tämä hyväksyttiin, jos vastauksesta kävi ilmi, että sillä tarkoitetaan todellisen tukivoiman ja lepokitkan resultanttivoimaa, muuten ei. Joissain oppimateriaaleissa on saman tapainen esimerkki, jossa sauvan pää ei ole kuitenkaan vapaasti seinää vasten vaan on kiinnitetty siihen esimerkiksi nivelellä. Tällaisessa tapauksessa sauvaan vaikuttaa kiinnityskohdassa vino voima.
Tehtävän 2. osassa piti määrittää sauvaan vaikuttavien voimien arvot silloin, kun narun ja sauvan välisellä kulmalla on eräs pienempi arvo kuin edellisen kohdan ääritapausta vastaava. Moni haksahti tässä olettamaan, että lepokitkalla on tässä tapauksessa sama arvo kuin edellisen kohdan ääritapauksessa. Lepokitkan arvohan muuttuu tilanteen mukaan ja asettuu siihen arvoon, joka vaaditaan tasapainon ylläpitämiseen.
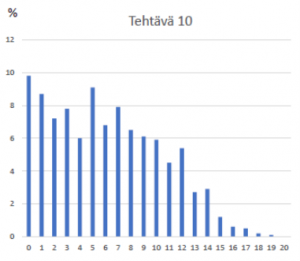
Tehtävä 10 Energiavarasto (7297 vastaajaa)
Ensimmäinen kohta oli perinteinen lämpöopin tehtävä, jossa piti hyödyntää lämpönä siirtyvän energian eli lämpömäärän ja lämpötilan muutoksen välistä yhteyttä ja määrittää annettujen tietojen perusteella lämpötilan muutos. Kokelaat osasivat tehdä tämän hyvin.
Kohdassa 10.2 suurin osa kokelaista laski lämpenevän veden tilavuuden muutoksen veden tilavuuden lämpötilakertoimen avulla. Tämä virheellinen ratkaisutapa antaa veden tilavuuden muutokseksi 2800 m2, kun todellinen muutos on noin 5400 m2 eli virhe on suuri. Tehtävässä oli tietoisesti valittu alkulämpötilaksi 1 celsiusastetta, jotta kokelaalla alkaisivat kellot soida ja hänen mieleensä palautuisi veden laajenemisen epälineaarisuus – veden tiheyden erikoinen käyttäytyminen alhaisissa lämpötiloissa on tuttu asia. Oikea tulos saadaan vertaamalla taulukoituja veden tiheyksiä alku- ja lopputilanteissa.
MAOLin taulukkokirjassa veden tilavuuden lämpötilakertoimelle annettu arvo pätee vain lämpötilassa 20 °C, ei lämpötilavälillä 20 °C–100 °C, kuten taulukon merkinnät antavat ymmärtää. Toisaalta annettu lämpötilaväli ei kata koko tehtävän lämpötila-aluetta, joten lämpötilakertoimen käyttö ei siltikään olisi ollut perusteltua. Toisaalla taulukossa on esitetty veden tiheyden kuvaaja lämpötilan funktiona, josta lämpölaajenemisen epälineaarisuus myös käy selvästi ilmi.
Kohdassa 10.3. vastauksesta piti ilmetä uusiutuvien energialähteiden ominaispiirre eli että niiden energiatuotanto riippuu luonnonolosuhteiden, kuten auringonpaisteen ja tuulen, lyhytkestoisista vaihteluista. Lisäksi piti mainita, että kun uusiutuvien energialähteiden osuus koko energiatuotannosta lisääntyy, pitää olosuhteiden vaikutus niiden energiatuotannon lyhytkestoisiin vaihteluihin tasata energiavarastojen avulla. Vuodenaikaisvaihteluiden tasaamista ei kelpuutettu, koska siihen osataan varautua perinteisen energiatuotannon keinoin.
Viimeisessä kohdassa veteen perustuvaa ja akkuihin perustavaa energiavarastointia pyydettiin vertaamaan toisiinsa energian tuotannon ja energian kulutuksen tasaamisen kannalta. Oleellisia ovat kapasiteetin, käyttönopeuden, käyttötarkoitusten ja energian siirtämisen helppouteen liittyvät erot. Aika moni oli lukenut tehtävän vähän huolimattomasti ja vastasi asian vierestä.
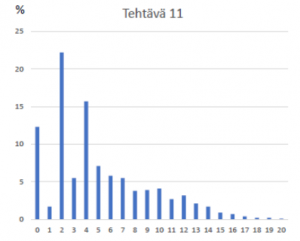
Tehtävä 11 Aurinkopaneeli (4776 vastaajaa)
Tässä tehtävässä kokelaalta vaadittiin kykyä soveltaa oppimaansa fysiikkaa aiheeseen, johon hän ei ole välttämättä törmännyt oppitunneilla. Puolijohteethan eivät ole kuuluneet LOPS:n keskeisiin asioihin (mutta onneksi kuuluvat uudessa LOPS:ssa!).
Ensimmäisessä kohdassa piti selittää, miksi paneelin suuntaaminen Aurinkoa kohti kasvattaa saatavaa sähkövirtaa. Tässä piti osata kertoa, että paneeliin osuvien fotonien määrä lisääntyy ja sitä myötä sähkövirtaa muodostavien elektroni-aukko-parien määrä.
Kohdissa 11.2. ja 11.3. piti sisäistää tehtävässä määritelty käsite spektrivaste, joka lienee ollut kaikille uusi ja kaiken kaikkiaan hieman mutkikas. Kysymykset osoittautuivat hankaliksi.
Kohdassa 11.4. piti kertoa, mitä suurimmalle osalle Auringon valon mukana kennoon osuvasta energiasta tapahtuu, kun kerrottiin kennon muuntamaan energiasta hyödynnettävään muotoon vain 15–20
Jos kokelas jaksoi tehtävän viimeiseen kohtaan, häntä odottivat siellä verrattain helpot neljä pistettä. Energian määrittäminen säteilyn aallonpituudesta oli helppo tehtävä, ja hyvin kokelaat sen osasivatkin tehdä.
Liitteet
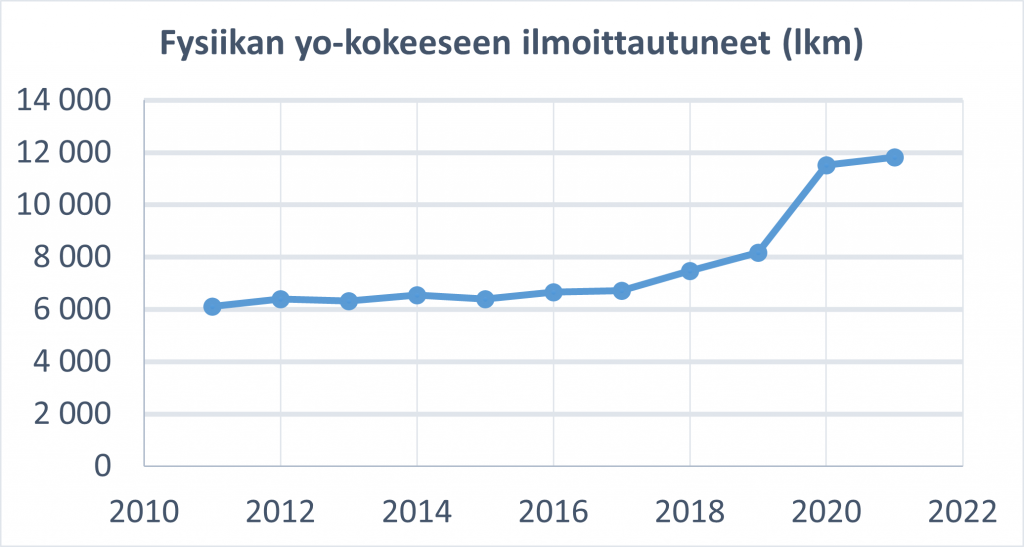
Kuva 1. Fysiikan ylioppilaskokeeseen ilmoittautuneiden määrä 2011–2021.
Kuva 2. Tehtäväkohtaiset pistejakautumat fysiikan ylioppilaskokeessa keväällä 2021.
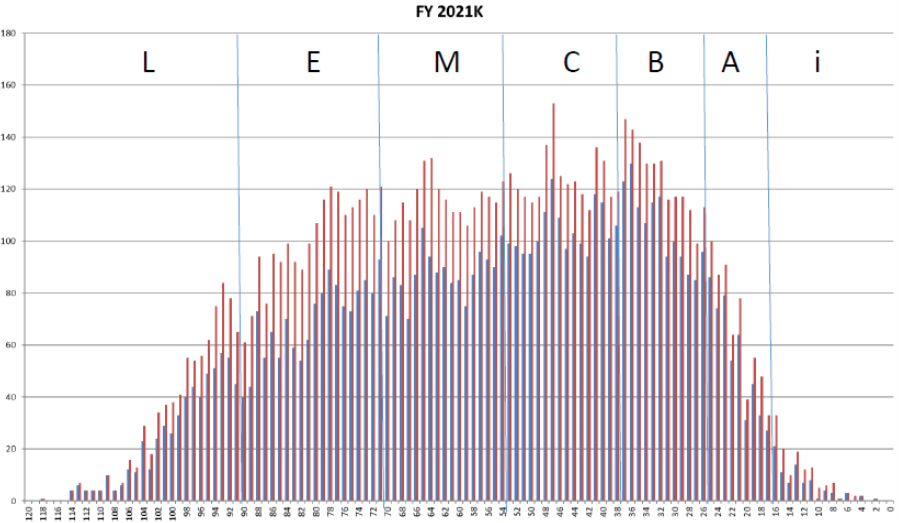
Kuva 3. Kevään 2021 fysiikan ylioppilaskokeen pistejakautuma. Siniset palkit vastaavat ensi kertaa kokeen kirjoittavia ja niiden jatkoina olevat punaiset palkit kokeen uusijoita. Taulukoon on merkitty myös arvosanojen pisterajat.