Kesäkuun pulmasivut: Ympyrän taittelu
Matemaattisten pulmien keksimisellä ei ole mitään rajaa. Geometristen pulmien ei tarvitse välttämättä olla piirtämistehtäviä, vaan paperintaittelukin käy. Näiden tehtävien idea on peräisin Michael Serran kirjasta Discovering Geometry, An Investigative Approach (2002).
Tulostettava versio pulmista (pdf)
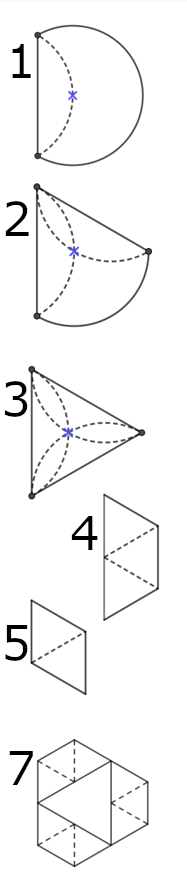
1. Leikkaa paperista suuri ympyrä. Taita yksi kehän piste keskipisteeseen. Taitos on alkuperäisen ympyrän jänne.
Kuinka kaukana se on keskipisteestä?
2. Taita syntyneen kaaren piste keskipisteeseen niin, että uuden taitokseen toinen päätepiste on edellisen taitoksen päätepiste.
Kuinka kaukana uusi taitos on keskipisteestä? Kuinka pitkiä taitokset ovat toisiinsa verrattuina? Perustele.
3. Taita paperi vielä kerran tekemiesi taitosten päätepisteiden kautta. Millaisen kolmion sait? Perustele.
4. Taita saamaasi kolmiota niin, että oikeanpuolimmainen kärki sattuu vasemmanpuolimmaisen pystysivun keskipisteeseen.
Millaisen kuvion sait? Kuvaile tarkasti.
5. Taita kuvion alanurkka alemman taitoksen reunaa pitkin.
Millainen kuvio syntyy nyt?
Avaa viimeinen taitos ja taita ylänurkka vastaavasti.
6. Avaa viimeiset taitokset niin, että saat taas kolmion. Voit taivuttaa sen taitoksia pitkin kolmiulotteisen kappaleen vaipaksi.
Mitä ominaisuuksia kappaleella on? Mikä se on nimeltään?
7. Avaa paperisi uudestaan kolmioksi. Taita kärjet taitoksien keskipisteisiin kuvan mukaisesti. Avaa nämä taitokset. Taivuta kappaleen vaipaksi.
Kuvaile tätä kappaletta.
8. Avaa kaikki taitokset ympyräksi asti. Millaisia kuvioita hahmotat taitoksista? Väritä korostaaksesi geometrisia havaintojasi.
Dimension pulmatehtävien ratkaisut MAOL ry:n sivuilta (vain jäsenille).
Lue täältä kaikki Dimension verkkolehdessä ilmestyneet pulmatehtävät
Tilaa Dimension uutiskirje – saat sähköpostiisi aina kuunvaihteessa koosteen tuoreimmista artikkeleista







