Joulupaketin sitomisesta ja kultaisesta leikkauksesta

Joulupaketin sitominen siten, että nauha kulkee viistosti kuvan 1 mukaisesti on tunnetusti tehtävä huolellisesti, jotta nauha ei pääse löystymään. Tarkastelemme seuraavassa, miten tämä sitominen on tehtävä. Olkoon suorakulmaisen särmiön muotoisen paketin särmät koko järjestyksessä $a,\ b\ \mathrm{\mathrm{ja}}\ c\ \ (a\geq\ b\geq\ c)$. Kuvassa 2 on paketti sivut levitettyinä auki. Sivu A on paketin etusivu, A2 on takasivu, A’ on etusivun peilikuva (jossa siis näkyy etusivun yläreunassa oleva nauhan kulku). Vastaavasti A2’ on takasivun A2 peilikuva. Jotta nauha ei pääsisi löystymään, pitää nauhan muodostaa tässä levityskuvassa janan lähtöpisteestä (kohdasta x ) samaan kohtaan sivulla A. Nauha tässä levityskuvassa ei siis saa olla muodostunut paloittain erisuuntaisista janoista. Kulmalle, jonka tämä nauha muodostaa paketin särmän kanssa, pätee kuvan 2 perusteella:
$$\tan{\alpha}=\ \frac{b+c}{a+c} \; \; \; \; (1)$$
Toisin sanoen suuntakulma, joka takaa nauhan pysymisen kireänä, määräytyy paketin sivujen mitoista. Esimerkiksi, jos $a:b:c=4:2:1$, on nauhan suuntakulman oltava $\alpha=\ \tan^{-1}{\left(3/5\right)}=31°$. Yhtälöstä (1) näemme myös, että suuntakulman suurin mahdollinen arvo on 45 °, mikä toteutuu tapauksessa $b=a$.
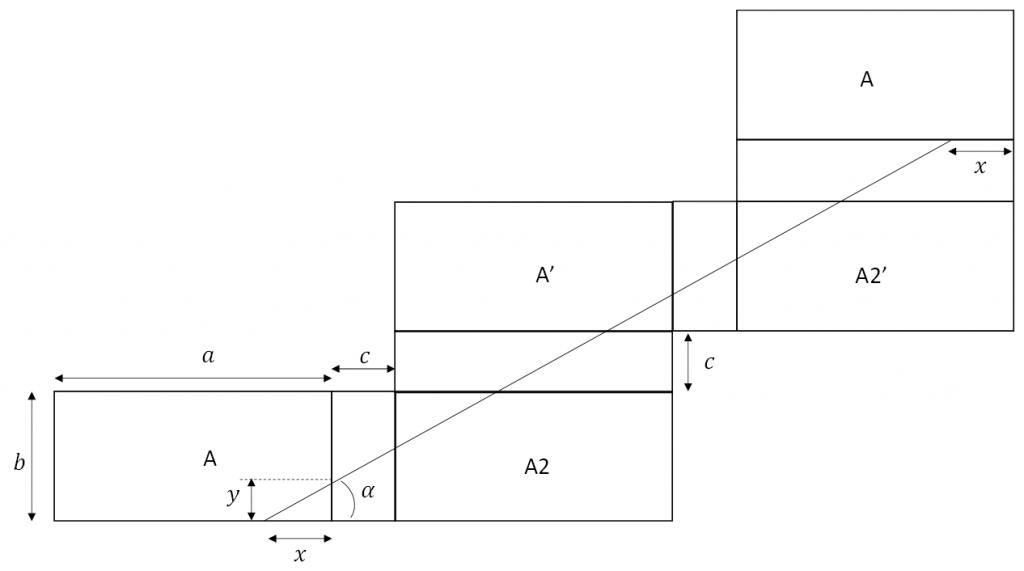
Kuva 2. Paketti sivut auki levitettyinä ja jatkettuina
Suuntakulma on siis yksikäsitteisesti määrätty paketin mittasuhteista, mutta kohta $x$, jossa nauha tulee paketin etusivulle, ei ole yksikäsitteinen, vaan sitä voidaan tietyissä rajoissa säätää. Kuvasta 2. näemme, että on oltava
$$\left(x+c\right)\ \tan{\alpha}<b \; \; \; \; (2)$$
jotta tämä viistomainen paketin sitomistyyli olisi mahdollinen (eli, että nauha ei ”putoa” paketin kulman yli). Sijoittamalla tähän yhtälö (1) saamme ehdon, että
$$x<\frac{ab-c^2}{b+c} \; \; \; \; (3)$$
Kun $b\in\left[c,a\right]$, pätee
$$f\left(b\right)=\ \frac{ab-c^2}{b+c}=a-\frac{a+c}{b+c}\ c\ \le\ a-c \; \; \; \; (4)$$
Jossa yhtäsuuruus pätee tapauksessa, jossa kaksi pisintä sivua ovat yhtä pitkiä, $b=a$ (eli suurin sivu on neliö). Toisaalta
$$f\left(b\right)=\ \frac{ab-c^2}{b+c}=a\ \frac{b}{b+c}-c\ \frac{c}{b+c}\ \ \geq\frac{a}{2}\ -c\ \frac{c}{b+c}\geq\ \frac{a-c}{2} \; \; \; \; (5)$$
Jossa yhtäsuuruus pätee taasen, kun kaksi lyhyintä särmää ovat yhtä pitkiä, $b=c$ (eli, että pienin sivu on muodoltaan neliö). Yhteensä siis
$$\frac{a-c}{2}\le\ \frac{ab-c^2}{b+c}\le\ a-c \; \; \; \; (6) $$
Yhtälöön (6) päätyy myös derivoimalla funktion $f\left(b\right)$ ja toteamalla funktion olevan monotonisesti kasvava funktio välillä $\left[c,a\right]$ ja funktion saadessa välin päätepisteissä yhtälön (6) antamat minimi ja maksimiarvot. Yhtälö (6) kertoo siis, että suurin mahdollinen arvo nauhan sijoituskohdalle x vaihtelee välillä $\left[\frac{a-c}{2},a-c\right]$ riippuen b:n arvosta välillä $\left[c,a\right]$.
Yhtälöstä (6), tai yhtä hyvin yhtälöstä (3), näkee sen, että kuution muotoiselle paketille $(a=b=c)$ tämä viistomainen paketin sitominen ei ole mahdollista.
Jos halutaan sellainen symmetria, että nauha jakaa kummatkin särmät $a$ ja $b$ samassa suhteessa, eli että
$$\frac{x}{a}=\frac{y}{b} \; \; \; \; (7)$$
Tällöin
$$\frac{b}{a}=\frac{y}{x}=\ \tan{\alpha}=\ \frac{b+c}{a+c} \; \; \; \; (8)$$
yhtälön (1) perusteella. Yhtälöstä (8) havaitaan, että tämä symmetrinen muoto ei onnistu mielivaltaiselle paketille, vaan ainoastaan paketille, jolle $a=b$, eli etusivultaan neliömäiselle paketille. Yhtälön (8) perusteella nauha muodostaa tässä tapauksessa etusivun särmien kanssa kulman $\alpha=\tan^{-1}{1}=\ 45°$.
Palataan takaisin yleiseen tapaukseen. Esteettisesti kaunein paketti saataisiin, jos nauha jakaisi pisimmän sivun kultaisen leikkauksen suhteessa, eli että
$$\frac{a}{a-x}=\ \frac{a-x}{x} \; \; \; \; (9)$$
Tämä johtaa tunnetusti toisen asteen yhtälöön, jonka välillä $0<x<a$ oleva ratkaisu on
$$x=\ \frac{3-\sqrt5}{2}\ a\approx0,382\ a \; \; \; \; (10)$$
Pidempi osa sivusta on tällöin
$$a-x=\ \frac{\sqrt5-1}{2}\ a\approx0,618\ a \; \; \; \; (11)$$
Sijoittamalla yhtälön (10) yhtälöön (3) saamme ehdon paketin mitoille, joille tämä kultainen leikkaus on mahdollinen
$$\left(\sqrt5-1\right)ab-\left(3-\sqrt5\right)ac>\ 2c^2 \; \; \; \; (12)$$
Skaalaamalla sivut b ja c pisimmällä sivulla a, eli käyttämällä muuttujia $\beta=b/a$ ja $\gamma=c/a$, saamme yhtälön (12) muotoon
$$\beta>\ \frac{\sqrt5+1}{2}\gamma\left(\gamma+\frac{3-\sqrt5}{2}\right) \; \; \; \; (13)$$
eli yhtälö kuvaa γβ-tasossa ylöspäin avautuvaa paraabelia. Kuvassa 3 viivoitettu alue kertoo, missä skaalattujen paketin mittojen (βγ) alueessa tämä kultaisen leikkauksen mukainen nauhan sijoittelu on mahdollinen.
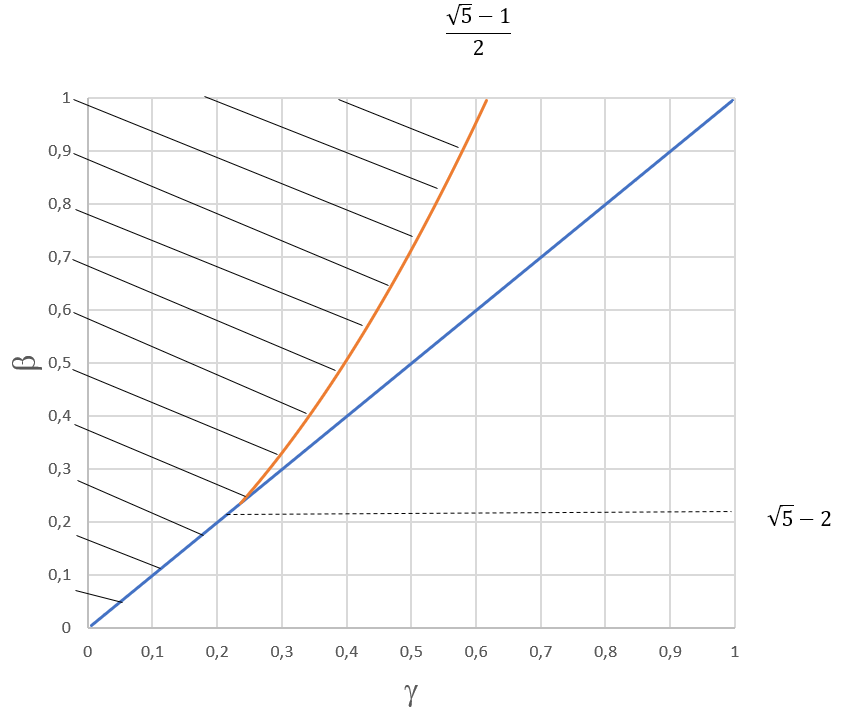
Kuva 3. Kultaisen leikkauksen mahdollistavat paketin mittasuhteet
Aluetta rajaa suorat $\gamma=0$, $\beta=1$ ja $\gamma=\beta$ sekä yhtälön (13) määräämä paraabeli. Kohdan, missä paraabeli kohtaa suoran $\beta=1$, saa laskettua sijoittamalla epäyhtälöä (13) vastaavaan yhtälöön arvon $\beta=1$ ja ratkaisemalla saadun toisen asteen yhtälön positiivisen ratkaisun. Ratkaisuksi tulee skaalamattomien mittojen $b$ ja $c$ avulla
$$\ c<\ \frac{\sqrt5-1}{2}\ a\ \approx0,618\ a \; \; \; \; (14)$$
jossa siis $b=a$.
Vastaavasti kohdan, missä paraabeli kohtaa suoran $\gamma=\beta$ saa ratkaistua sijoittamalla epäyhtälöä (13) vastaavaan yhtälöön arvon $\beta=\gamma$ ja ratkaisemalla nollasta poikkeavan juuren. Tästä saadaan tulos
$$b=\ c<\ \left(\sqrt5-2\right)\ a\ \approx0,236\ a \; \; \; \; (15)$$







