It stops – se pysähtyy

Opetus

18.5.2021

Pysähtymisessä on jotain salaperäistä. Se tuntuu lopulliselta, mutta joskus se on vain väliaikaista. Joskus mikään ei pysähdy, vaan jatkuu vain toisenlaisena. Silloin ”it stops” pysäyttää lukijan tai kuulijan ajattelemaan, mitä sitten seuraa.

Pysähtymisestä kirjoittaa intialainen Shakuntala Devi (1929–2013) kirjassaan Figuring [1], kun hän kuvailee ykkösen kykyä luoda palindromilukuja. Jono on ehkä sinulle tuttu:

1 · 1 = 1

11 · 11 = 121

111 · 111 = 12321

1111 · 1111 = 1234321

…

111111111 · 111111111 = 12345678987654321

”At that point it stops”, sanoo hän. Hänen oli helppo sanoa niin, sillä hän pystyi laskemaan päässään sekunneissa, mitä tapahtuu seuraavaksi. Miksi hän lopettaa juuri siihen? Vastaus ei selviä ihan millä tahansa laskentavälineellä, sillä läheskään kaikki niistä eivät pysty enää näyttämään seuraavaa 19-numeroista tuloa kokonaisuudessaan. Tarvitaan erikoisväline [2], joka kertoo että

1111111111 · 1111111111 = 1234567900987654321

11111111111 · 11111111111 = 123456790120987654321

…

Kerrottavia voi pidentää rajattomasti, ja ne voi aina kertoa keskenään. Siis mikään ei pysähdy tai pääty. Tulot eivät vain enää ole palindromeja.

Pyörimisen pysähtyminen?

Konkreettisessa liiketilanteessa luulisi olevan selvää, mikä on pysähtymistä ja mikä ei, mutta eipä vainkaan. Selittäessään pyörän pyörimistä tasaisella alustalla [3] MIT:n luennoitsija Dennis Auroux piirtää kehäpisteen ratakäyrän, sykloidin, alimpaan kohtaan pisteen ja sanoo, että ”it stops here”. Järki ja arkikokemus sanovat, että eihän siinä mikään pysähdy, vaikka kehäpisteen nopeus onkin hetkellisesti nolla. Pyörä jatkaa pyörimistään ja juna tai auto etenemistään tasaisella vauhdilla.

*Kuva 1: Tasaisesti etenevän pyörän pyöriessä tasaisella alustalla kehäpisteen rata on sykloidi. Sen nopeus radan alimmassa kohdassa on 0 ja kiihtyvyys kohtisuoraan ylöspäin.* *(Ruudunkaappaus Dennis Auroux’n videoluennosta, MIT OpenCourseWare CC-BY 4.0.)*

Liukuva kappale

Esimerkkejä päänvaivaa aiheuttavista jatkumistilanteista ei tarvitse hakea kvanttifysiikasta tai planeettaliikkeestä. Quanta-lehden kolumnisti Pradeep Mutalik esitti joulukuussa 2019 seuraavan probleeman [4]:

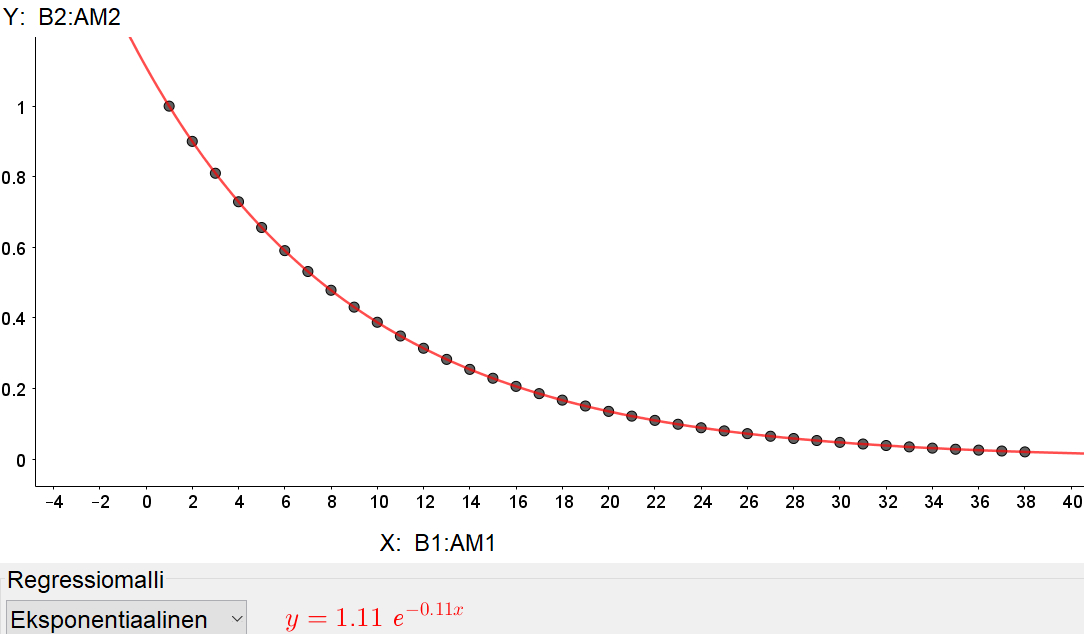
Kappale liukuu tasaisella pinnalla alkunopeudella 1. Jokaisella yhden yksikön pituisella matkalla sen nopeus pienenee yhdellä kymmenesosalla siitä, mitä se oli kunkin matkayksikön alussa. Kuinka pitkän matkan kappale kulkee ennen pysähtymistään?

Artikkelin loppuun liitetyssä pitkässä kommentissa Jonathan Vercruysse kirjoittaa, että ”object will never stop”. Mitä mieltä sinä olet? Mutalikin vastaus julkaistiin kuukautta myöhemmin [5].