Helmikuun pulmasivut: Collatzin konjektuuri
Helmikuun pulmatehtävissä tutustutaan Collatzin konjektuuriin eli otaksumaan.
Collatzin otaksuma on positiivisia kokonaislukuja koskeva väite. Sen mukaan päädytään loputtomaan silmukkaan, lähdettiinpä mistä luvusta n tahansa, jos edetään niin, että
1o luku n korvataan luvulla 3 n + 1, jos se on pariton tai
2o luku n jaetaan luvulla 2, jos se on parillinen
ja samoja sääntöjä sovelletaan tuloksena olevaan lukuun yhä uudestaan. Esimerkiksi luvusta 6 aloitettaessa saadaan
6 3 10 5 16 8 4 2 1 4 2 1 4 2 1 …
Jos halutaan kirjoittaa algoritmi lukujen laskemiseksi, niin tarvitaan kolmas sääntö
3o lopeta, kun tulet lukuun 1.
Kustakin luvusta saadaan siis siitä alkava, ykköseen päättyvä äärellinen lukujono.
Otaksuman esitti saksalainen matemaatikko Lothar Collatz (1910–1990) vuonna 1937. Näennäisestä yksinkertaisuudestaan huolimatta sitä ei ole todistettu oikeaksi eikä vääräksi. Lukuja on tutkittu yksitellen lähes kaksi triljoonaa ja ne kaikki toteuttavat Collatzin otaksuman. Aluksi jonot ovat suhteellisen lyhyitä, mutta esimerkiksi jo luvusta 27 alkavassa jonossa on enemmän kuin sata lukua.
Collatzin jonojen luvuista voidaan piirtää verkkomainen kartta (Elsa Moreira 2022: 5 problèmes de mathématiques que personne n’a réussi à résoudre):
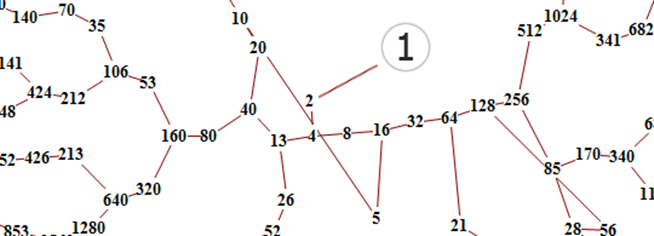
Tehtävät:
1. Laadi parhaiten osamaallasi tai mielestäsi tähän ongelmaan parhaiten sopivalla ohjelmointivälineellä algoritmi, joka tuottaa ykköseen päättyvän Collatzin jonon, kun lähdetään positiivisesta kokonaisluvusta.
2. Tuota algoritmillasi Collatzin jonot 1–10. Kuinka pitkä on pisin jono?
3. Järjestä Collatzin jonoissa 1–10 jonoissa esiintyvät luvut kuvaksi, kartaksi tai taulukoksi järjestelmällisesti (eikä vain epämääräiseksi verkoksi niin kuin edellisessä kuvassa) niin, että kukin luku esiintyy vain kerran.
4. Piirrä samaan kuvioon graafit Collatzin jonoista 1–10. Mikä on suurin luku, joka esiintyy näissä jonoissa?
5. Tuota algoritmillasi luvusta 27 alkava jono. Kuinka monta lukua siinä on?
6. Jatka tutkimuksia kymmentä suuremmista luvuista alkavista Collatzin jonoista.
Keksi omia tehtäviä.
Dimension pulmatehtävien ratkaisut MAOL ry:n sivuilta (vain jäsenille).
Lue täältä kaikki Dimension verkkolehdessä ilmestyneet pulmatehtävät
Tilaa Dimension uutiskirje – saat sähköpostiisi aina kuunvaihteessa koosteen tuoreimmista artikkeleista







