Hammastikkutehtävä
Matematiikka ei ole vain hyödyllinen tieteenala, vaan sen sokkeloissa syntyy paljon innostavaa pikku pohdittavaa. Niin kuin nyt tämäkin Samuli Siltasen tiedekanavallaan esittämä jono 3, 7, 11, 15, …
Aiheen löysin avoimesta Facebook-ryhmästä MAOL eKerho [1]. Siellä Samuli Siltanen on kertonut 9.1.2021 kolmesta matikkapulmasta. Viimeinen niistä synnytti varsinaisen ratkaisun etsimisen ohella monenlaista pohdintaa.
Siltanen esittää videollaan Samun tiedekanava [2] jonon 3, 7, 11, 15 ja kysyy jonon seuraavaa jäsentä. Seuraavassa kuvassa hän hylkää raa’asti vastauksen 19, niin kuin se olisi väärä. Mistään hänen antamastaan vihjeestä ei voi kuitenkaan päätellä, etteikö kyseessä olisi aritmeettinen jono. Hän jopa jättää näyttämättä jonon kaksi ensimmäistä jäsentä.
Professorin ajatuksenjuoksu on kerkeämpää ja hänen älylliset askeleensa pitemmät kuin koululaisen tai tavallisen opettajan. Hänellä on on nimittäin mielessään ihan toinen jono: suorakulmaiseen koordinaatistoon rakennettu hammastikkujono (toothpick sequence). Sen seuraava jäsen onkin 23 ja sitä seuraava 35 (OEIS A139250).
Sitä professori ei tule ajatelleeksi tai ei halua maallikoille paljastaa, että kuusikaan jäsentä ei määrittele hänen tarkoittamaansa jonoa yksikäsitteisesti. Siihen tarvittaisiin ainakin 12 jäsentä:
0, 1, 3, 7, 11, 15, 23, 35, 43, 47, 55, 67, …
Nimittäin säännöllisten kuusikulmioiden muodostamaan vinokulmaiseen koordinaatistoon rakennettu hammastikkujono (OEIS 182634) eroaa edellisestä vasta 12. jäsenestä lähtien:
0, 1, 3, 7, 11, 15, 23, 35, 43, 47, 55, 71, …
Vaikka hammastikkujono näyttää etenevän kummallisen epäsäännöllisesti, niin se rakentuu hyvin konkreettisesti. Otetaan jana (hammastikku). Sen kumpaankin päähän pannaan kohtisuoraan poikittain yksi tikku (kuva 2). Saadun kuvion vapaisiin päihin pannaan taas tikut poikittain. Jatketaan näin niin pitkälle kuin jaksetaan.
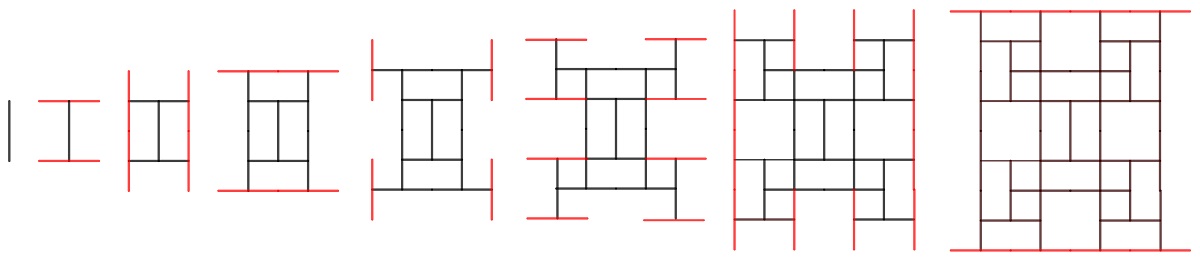
Analyyttistä ratkaisua jonon n:nnelle jäsenelle (hammastikkujen lukumäärälle) ei tunneta. Jonoa on kuitenkin tutkittu kymmeniin tuhansiin asti Table of n, a(n) for n = 0..65535 [3]. Sadas jäsen on 4 903, tuhannes 546 183 ja kymmenestuhannes 49 603 375. Jonon peräkkäisten jäsenten erotus (lisättävien hammastikkujen määrä, OEIS A139251) vaihtelee voimakkaasti (kuva 3). Välillä 0–10000 se on suurimmillaan 419 328 ja pienimmillään 4 aina, kun kuvion järjestysluku on kakkosen potenssi (esimerkiksi kuviot 2, 4 ja 8 kuvassa 2 ja kuva 5).
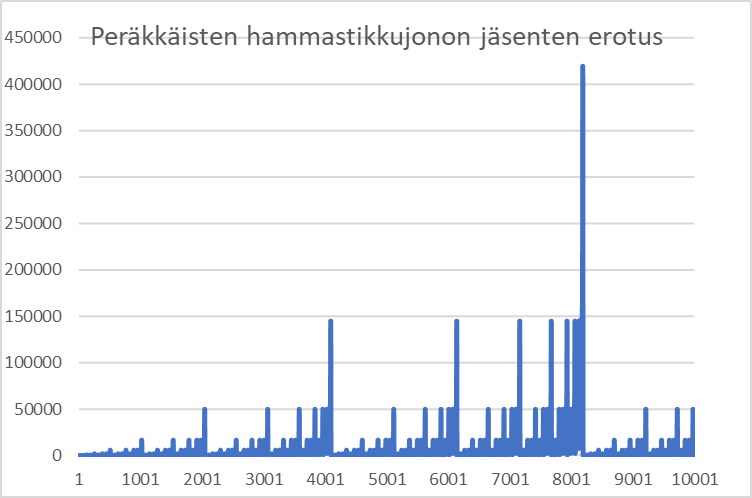
Peräkkäisten jäsenten erotuksen voimakkaassa vaihtelussa voi havaita tietynlaista jaksollista säännöllisyyttä. Tämä näkyy selvästi jonon jäsenten kasvukäyrän muodossa ja sisäisessä rakenteessa (kuva 4). Siinä olen havaitsevinani fraktalisoituvia piirteitä, sillä kasvu kiihtyy pienillä ja vielä pienemmillä väleillä samaan tapaan kuin koko käyrän kasvu.
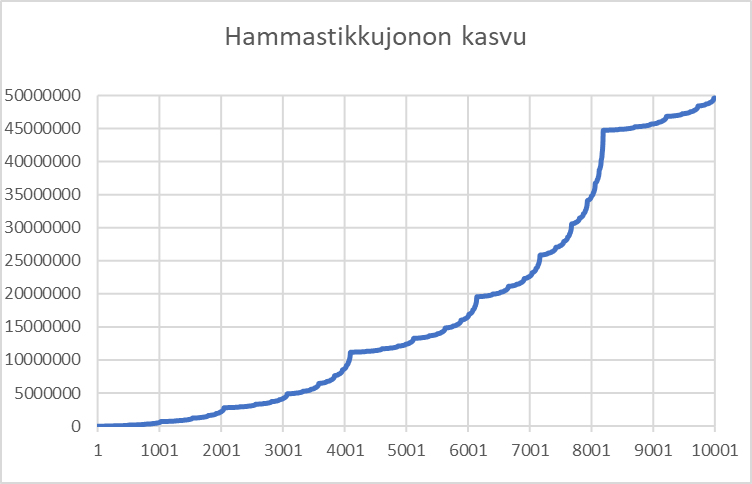
Hammastikkukuvioita voi tutkia myös verkossa [4] Explorations of A139250 the toothpick sequence and other toothpick-like sequences. Fraktalisoitumisen olen näkevinäni myös rakentumiskuviossa (kuva 5).

Hammastikkujonosta voidaan rakentaa muita jonoja, esimerkiksi
1, 3, 11, 43, 171, 683, 2731, 10923, 43691, 174251, 699051, 2796203, 11184811, … ja
1, 1, 2, 2, 3, 3, 4, 5, 5, 6, 6, 7, 8, …
Edellistä jonoa OEIS ei tunne lainkaan. Mikähän se mahtaisi olla? Jälkimmäinenkään ei siellä ole juuri tällä tavalla määriteltynä, vaikka on muutamia muita jonoja, joissa on alussa samat 13 jäsentä. Kun näet molemmat jonot yhdessä, niin havaitset helposti (?), miten jälkimmäinen jono on muodostettu. Ilman sitä muodostumisperiaatetta olisi varmaan vaikea keksiä. Kuvaile se sanoin niin, että tulos on yksikäsitteinen.
Lähteet:
[1]MAOL eKerho https://fi-fi.facebook.com/groups/155873227301/, viitattu 3.2.2021
[2] Samun tiedekanava https://www.youtube.com/watch?v=iFbZzlO2Uaw&feature=youtu.be, viitattu 3.2.2021
[3] Table of n, a(n) for n = 0..65535 https://oeis.org/A139250/b139250.txt, viitattu 3.2.2021.
[4] Explorations of A139250 the toothpick sequence and other toothpick-like sequences, https://oeis.org/A139250/a139250.anim.html, viitattu 3.2.2021







