Graafiteorian oppimateriaalia

Viime vuonna sain valmiiksi pro gradu -tutkielmani ”Graafiteorian oppimateriaalia”. Tutkielma tarjoaa oppimateriaalia graafiteoriasta kiinnostuneille ja se on sovellettavissa esimerkiksi osaksi diskreetin matematiikan kurssia. Graafiteoria tarjoaa vaihtoehtoisen, visuaalisen tavan monien konkreettisten ongelmien ratkaisuun. Tässä artikkelissa esittelen muutaman klassisen graafiteorian sovellutuksen.

Mitä graafiteoria on?

Graafiteoria on matematiikan ala, joka tutkii objektien välisiä suhteita graafien eli matemaattisten mallien avulla. Graafit koostuvat yksinkertaisuudessaan pisteistä ja niitä yhdistävistä viivoista. Esimerkiksi keskenään kilpailevista eläinlajeista voidaan muodostaa graafi. Pisteillä merkitään lajia ja viiva kahden lajin välillä ilmaisee, että lajit ovat keskenään kilpailevia.

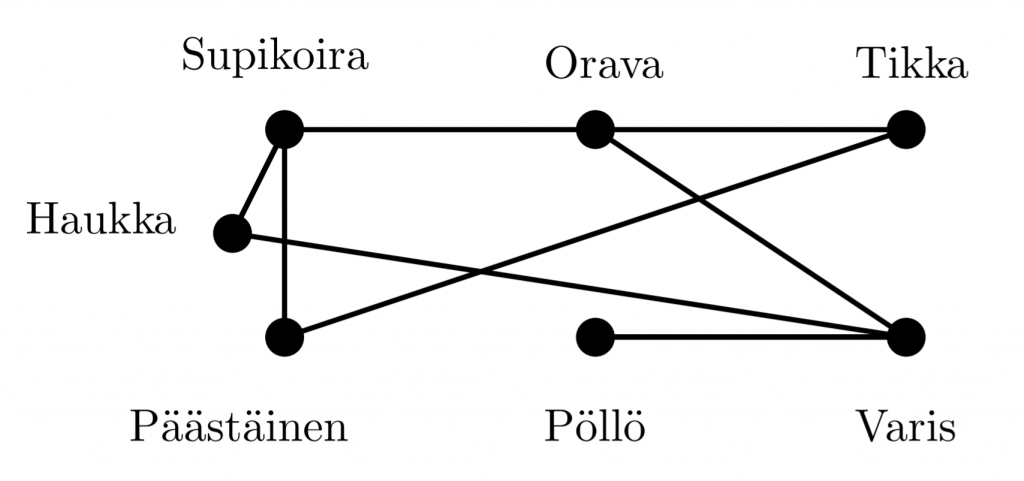
Mallinnuksen lisäksi graafien avulla voidaan pyrkiä ratkaisemaan monenlaisia ongelmia. Esimerkiksi graafin viivoja pitkin voidaan pyrkiä muodostamaan haluttuja reittejä. Graafin pisteitä ja viivoja voidaan värittää eri säännöin. Graafin viivoihin voidaan liittää lukuja, joilla voidaan esimerkiksi mallintaa kilometrejä kaupunkien välillä. Pro gradussani esittelen viidessä kappaleessa tällaisia sovellutuksia ja yhteensä sata tehtävää ratkaisuineen niihin liittyen.

Köninbergin siltaongelma

Graafiteorian voidaan sanoa alkaneen Köningsbergin siltaongelmasta. Pregelin joki jakoi Köningbergin (nykyinen Kaliningrad) kaupungin neljään osaan. Näitä osia yhdisti seitsemän siltaa. Tarinan mukaan kaupunkilaiset yrittivät löytää kotioveltaan reittiä, joka kulkisi jokaisen sillan yli vain kerran ja palaisi kotiovelle. Leonhard Euler osoitti tällaisen reitin mahdottomaksi muodostamansa graafin avulla. Hänen mukaansa on nimetty graafit, jotka sisältävät piirin, jossa kuljetaan jokaisen viivan kautta täsmälleen kerran.

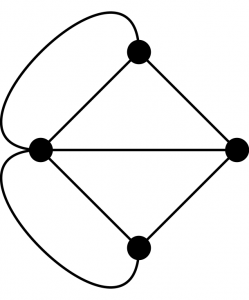
Kuvateksti: Tämä graafi kuvaa Köningsbergin siltaongelmaa. Pisteet ovat maa-alueita ja viivat niiden välisiä siltoja. Kahdesti kahden maa-alueen välillä on kaksi siltaa.

On perin helppoa selvittää, onko graafi Eulerin graafi. Mikäli kaikki graafin pisteet ovat päätepisteinä parilliselle määrälle viivoja, graafi on Eulerin graafi. Köningsbergin siltoja kuvaava graafi ei ole Eulerin graafi, sillä esimerkiksi oikeanpuoleisin piste on päätepisteenä kolmelle viivalle.

Graafien värittäminen

Kenties nimekkäin graafien sovellutuksista on karttojen värittämiseen liittyvä neliväriongelma. Vuonna 1852 Francis Guthrie huomasi, että kaikki Englannin maakunnat voitiin värittää neljällä värillä siten, että vierekkäisillä maakunnilla ei ollut samaa väriä. Heräsi kysymys, voidaanko kaikki mahdolliset kartat värittää neljällä värillä. Tilannetta voidaan havainnollistaa graafeilla, joissa pisteet ovat maita ja viivat maiden välisiä rajoja. Mikäli kahden pisteen välillä on viiva, eivät pisteet voi olla saman värisiä. Vasta vuonna 1976 Wolfgang Haken onnistui osoittamaan tietokonemallinnuksella, että kaikki kartat ovat väritettävissä neljällä värillä.

Graafien värittämisessä on mielekästä tutkia, mikä on vähin mahdollinen määrä värejä, joilla graafi saadaan väritettyä. Pienintä mahdollista määrää värejä, jotka tarvitaan graafin värittämiseen, kutsutaan graafin väriluvuksi. Sen selvittämiseksi on kehitetty algoritmeja, mutta ei sellaista, joka varmasti tuottaisi vähimmän määrän kaikkien graafien kohdalla. Graafien värittämisellä voidaan mallintaa esimerkiksi risteyksen liikennevaloja. Pienimmän väriluvun avulla on mahdollista etsiä vähin määrä liikennevalojen tilanteita, joilla liikenne sujuu kolareitta.

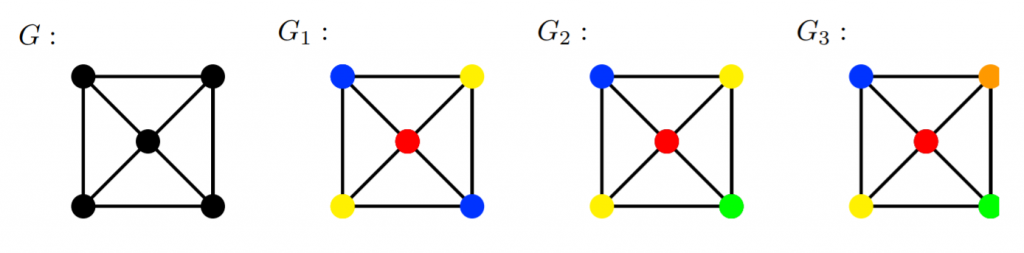
Kuvateksti: Ohessa on graafi G ja sen kolme eri väritystä. Graafin värittämiseen tarvitaan vähintään kolme väriä, joten sen väriluku on kolme.

Hamiltonin graafi

Vuonna 1856 irlantilainen matemaatikko William Rowan Hamilton kehitti Icosian -pelin. Se koostui puusta tehdystä tasoon piirretystä dodekaedrista, jonka jokainen kulma oli nimetty kuuluisan kaupungin mukaan. Dodekaedrissa on 12 viisikulmaista tahkoa. Pelin tarkoituksena oli ”kulkea maailman ympäri” jokaisen kaupungin kautta vain kerran ja palata takaisin päämäärään. Pelillään Hamilton antoi nimen kaikille sellaisille graafeille, joista löytyy piiri, jossa on kaikki graafin pisteet täsmälleen kerran.

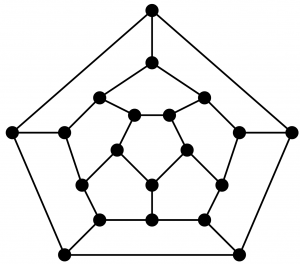
Valitettavasti peli ei ollut menestys, sillä tehtävä on melko helppo ratkaista. Voit kokeilla löytää ratkaisun itse oheisen kuvan avulla. Aloita yhdestä pisteestä, piirrä kynällä reitti, joka kulkee jokaisen pisteen kautta vain kerran palaten lopulta aloittamaasi pisteeseen.

Tutkielmani esittelee myös muun muassa graafien dominointia, painotettuja graafeja sekä virittäviä puita. Sen esittelemät sovellutukset ovat helposti ymmärrettävissä, sillä ne ovat esitettyinä graafein visuaalisesti. Sovellutukset ovat usein myös perin intuitiivisia. Pro gradu on löydettävissä sivustolta https://trepo.tuni.fi/handle/10024/105781.