Askartelua ja aivojumppaa: pop up 2

Pop up -kortti tehdään leikkaamalla ja taittamalla kaksinkerroin taitettua paperi- tai kartonkiarkkia ja mahdollisesti liimaamalla lisäosia. Sakset riittävät tavallisesti, mutta tarkkaan työskentelyyn tarvitset terävän askarteluveitsen tai pienen mattoveitsen ja tukevan leikkuualustan. Tarkkaan taittamiseen tarvitset myös viivaimen, jota pitkin taittaa.

Tehtävä 1: yksinkertainen pop up -kuutio

Tee kohtisuoraan taitetta vastaan kaksi leikkausta, jotka ovat yhtä pitkiä kuin niiden välimatka. Taita leikattu alue ulos kortista viivainta vasten.   Kuutiossasi on nyt oikeastaan vasta kaksi sivutahkoa, mutta se hahmottuu jo kuutioksi ja taittuu litteäksi kortin mukana. Tästä on monia jatkotyöversioita. Katso esimerkiksi jutun viimeistä kuvaa.

Tehtävä 2: pop up -kuutio, jossa on kaksi lisätahkoa

Kaksi muuta sivutahkoa saat liimaamalla. Varaa lisätahkoon liimausvarat. Taita lisätahko ennen liimaamista lävistäjää pitkin niin, että liimausvarat taittuvat päällekkäin. Taitoksen ansiosta kuutio taittuu litteäksi korttia taitettaessa. Voit vielä liimata korttiisi kortin kokoisen ulkokannen niin, että saat kuutiollesi loputkin sivutahkot. Liimaa se kiinni vain etukanteen, jotta pääset kuutiosi sisään.

Tehtävä 3: nelisivuinen pyramidi

Pyramidikortin tekeminen onnistuu helpoimmin niin, että leikkaat pyramidin vaipan erikseen. Muista jättää liimausvarat vaipan reunaan ja pohjan kahteen vierekkäiseen sivuun. Liimaa pyramidi ensin kokoon sivusärmästään. Liimaa sitten pyramidi korttiin niin. että pyramidin sisäpuolelle taitetut liimausvarat jäävät taitteen eri puolille ja että vapaaksi jäävä kärki on lähellä kortin reunaa. Kohdista kärjet tarkasti kortin selkätaitteeseen. Kiinniliimattavan kärjen puolelle pitää jättää enemmän tilaa kuin vapaan kärjen puolelle, sillä pyramidi taittuu  siihen suuntaan, kun kortti taitetaan kokoon. Pyramidin kärki saattaa nimittäin tulla ulos kansien välistä, kun kortti taitetaan kiinni, jos pyramidi liimataan keskelle korttia. Jos käytät jäykkää kartonkia, niin tee kaikki taitokset aina kumpaankin suuntaan. Sillä tavalla saat joustavat taitokset, joihin ei jää jännityksiä.

Miten tekisit kolmisivuisen pyramidin? Voitko tehdä pyramidin aina sivujen lukumäärästä riippumatta? Miten voit vaikuttaa pyramidin kärjen terävyyteen?

Tehtävä 4 vaihtoehtoinen kartiokortti

Nelisivuisen pyramidin voit tehdä myös yhdellä, kortin selkätaitetta vastaan kohtisuoralla leikkauksella ja kahdella samasta taitteen pisteestä alkavalla taitoksella. Pohja on avoin, mutta voit tehdä sen liimaamalla erillisen pohjatahkon samalla tavalla kuin tehtävässä 2. Kartion kaksi muuta sivutahkoa ovat myös avoimia, toistaiseksi vain reikä taittokortissa.

Kun tutkit kartiota tarkemmin, niin huomaat, että pohja ei ole kohtisuorassa kortin kansia vastaan, kun kortti on avattu 90 asteen kulmaan. Onko itse kartio kuitenkin suora? Perustele.

Onnistuuko muun kuin nelisivuisen pyramidin tekeminen tällä tavalla?

Millainen kartiostasi tulee, jos leikkaus ei olekaan kohtisuorassa kortin selkätaitetta vastaan? Onnistuuko  litteäksi taittuvan pohjan liimaaminen myös tällöin? Mihin suuntaan on leikattava, jotta kartion pohja olisi kohtisuoraan kortin kansia vastaan, kun kortti on avattu 90^o?

Katkaistun kartion saat kahdella eripituisella leikkauksella ja niiden päät yhdistävillä kahdella taitoksella.

Tehtävä 5: kuutiokortin mallinnuksia

Leikkaaminen ja liimaaminen on konkreettinen tapa tehdä matematiikkaa. Tuotosten mallintaminen vaatii oman suunnittelunsa. Sen voit tehdä esimerkiksi 2D- tai 3D-Geogebralla.

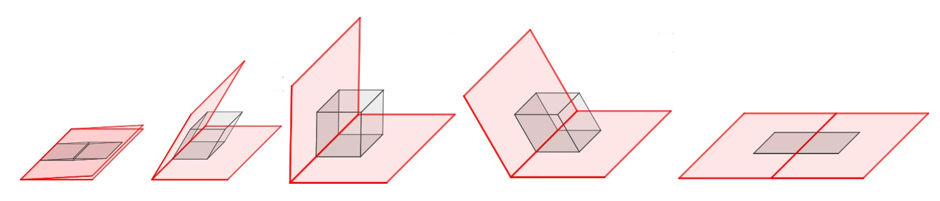
2D-Geogebralla tehty matletti on osoitteessa https://www.geogebra.org/m/kafpqmkh.

Tällä kuvalla on kiinteä projektiosuunta, vaikka kuva muuten onkin dynaaminen.

3D-Geogebralla tehty matletti on osoitteessa https://www.geogebra.org/m/qfdfqh2a.

Kuvaa voit pyörittää vapaasti niin kuin mitä tahansa kappaletta.

Tehtävä 6: lisää katsomista ja lukemista

Katso esimerkiksi Willy Kjellstromin The Math in Pop Ups -sivua http://www.willykjellstrom.com/portfolio_page/pop-up-mathematics/

Math Munch -sivustolla https://mathmunch.org/2013/08/29/moma-pop-up-books-and-a-game-of-numbers/ kerrotaan New Yorkin Modernin taiteen museosta MoMasta ja siellä on linkki videoon https://www.youtube.com/watch?v=beERPEgsjaI.

Esiteltävät työt eivät ole enää oppituntiharjoituksia, mutta ne osoittavat, miten monimutkaisia pop up ‑kortteja voidaan tehdä.

Tämä on jutun toinen, toiminnallinen osa. Ensimmäinen, aiheeseen johdatteleva osa ilmestyi 21.2.2020. https://www.dimensiolehti.fi/askartelua-ja-aivojumppaa-pop-up-1/