Kolme tehtävää matematiikan rakastajilta
Rakastan matematiikka on avoin facebook-ryhmä. Siellä on kaikenlaista puhetta matematiikasta, välistä myös tehtäviä ryhmän jäsenten iloksi ja virkistykseksi. Kesän aluksi niitä tuli päivittäin, esimerkiksi seuraavat kolme. Ryhmän löydät osoitteesta https://www.facebook.com/groups/113557938672387/.
Allin ympyrä
Matikkatäti Alli Huovinen julkaisi 2.6.2021 facebook-ryhmässä Rakastan matematiikkaa tehtävän, joka keräsi nopeasti kolmattakymmentä kommenttia. Kukaan ei tarjonnut sellaista ratkaisua, jonka nykyiset koulumatematiikan työvälineet sallisivat.
Tehtävä kuului näin:
Määritä sen ympyrän yhtälö, joka kulkee pisteiden (6, 1), (2, 3) ja (4, 5) kautta
Hyvin tavanomainen analyyttisen geometrian oppikirjatehtävä.
Vastaajat tuntuivat olevan hyvin perillä siitä, miten tällaiseen tehtävään käydään käsiksi koulumatematiikassa. Otetaan ympyrän yhtälö, sijoitetaan siihen pisteiden koordinaatit piste kerrallaan ja ratkaistaan ympyrän yhtälön kertoimet saadusta kolmen yhtälön yhtälöryhmästä.
Kukaan ei tarttunut tarjolla olevaan geometriseen ratkaisuun. Etsitään piirtämällä piste, joka on yhtä kaukana annetuista pisteistä. Se on ympyrän keskipiste. Sitten voidaan laskea säde ja muodostaa ympyrän yhtälö.
Vielä helpompi olisi ollut käyttää Geogebraa. Sen vakiotoimintona on kolmen annetun pisteen määrittämän ympyrän piirtäminen. Samalla ohjelma näyttää myös ympyrän yhtälön.
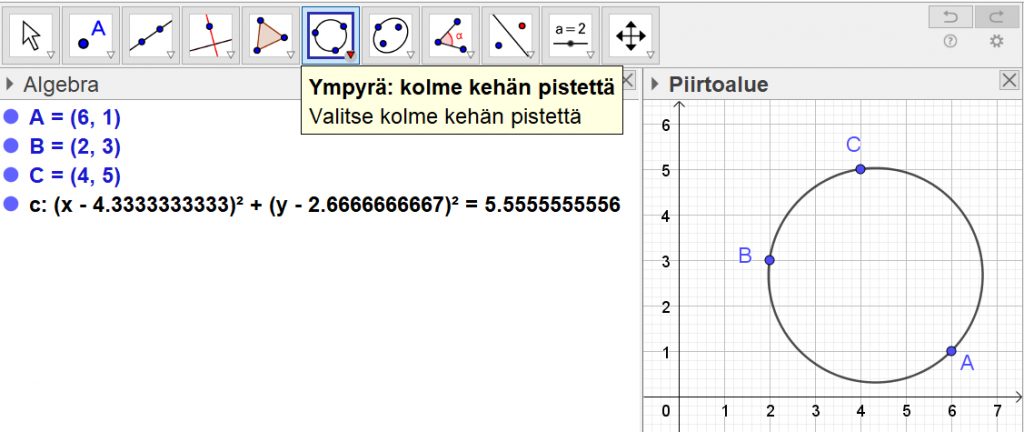
Ainoa muodollinen heikkous on, että Geogebra näyttää yhtälön kertoimet desimaalilukuina. Tässä tapauksessa kaikki kertoimet näyttävät olevan päätymättömiä desimaalilukuja, joiden jakson pituus on 1, siis rationaalilukuja. Jos vielä sattuu muistamaan, miten tällainen desimaaliluku muunnetaan murtoluvuksi, niin yhtälö on helppo kirjoittaa:
$\left(x-\frac{13}{3}\right)^2+\left(y-\frac{8}{3}\right)^2=\frac{50}{9}.$
Yhtälöä voi sitten itse kukin sievennellä haluamaansa muotoon. Jos haluaa vielä muodollisen todistuksen, niin ei auta kuin sijoittaa koordinaatit yhtälöön piste kerrallaan. Geogebrassa on muuten toiminto ”Kahden objektin välinen suhde”, joka tarkistaa ilman käyttäjän laskuja, onko piste suoralla.
Koira ja isäntä
Matti Pylvänäinen julkaisi 3.6.2021 tehtävän, jonka idean hän sanoi saaneensa ulkoilulenkillä. Tehtävä kuului näin:
Isäntä seisoo suorakulmaisen kentän kulmassa A. Hänen koiransa istuu kentän kulmassa B. Kulmien välimatka on 100 metriä. Isäntä lähtee kävelemään kohti kulmaa D tasaista 6 km:n tuntivauhtia. Samalla hetkellä koira lähtee seuraamaan isäntäänsä tasaista 12 km:n tuntivauhtia siten, että se juoksee koko ajan isäntää kohti. Kun koira lopulta saavuttaa isäntänsä, niin kuinka pitkän matkan isäntä on kulkenut ja koira juossut?
Konkreettinen tilanne, johon ei ole ilmeistä ratkaisua koulumatematiikan menetelmävarastossa.
Ensimmäisen ratkaisun ehdottaja tarjosi menetelmäksi vektoreita ja differentiaaliyhtälöparia. Tekstissään hän mainitsi lähtöarvot 21,6 m/s (isäntä) ja 43,2 m/s (koira), jotka ylittävät täysin kummankin kulkijan kyvyt.
Toinen ratkaisija mallinsi tilanteen graafisesti. Tulokset ovat isännälle noin 130,2 m ja koiralle 63,5 m. Vähän myöhemmin hän sanoo toisessa viestissään, että ”funktiolle löytyi symbolinenkin esitys”. Analyyttisen ratkaisun tulokset ovat 400/3 m ≈ 133 m ja 200/3 m ≈ 67 m.
Tilanne on mallinnettavissa luontevasti kilpikonnagrafiikalla. Käytin FMSlogoa. Kun lähtöpaikkojen ero on 100 (m) ja koiran nopeus on kaksinkertainen isännän nopeuteen verrattuna (kuva 2), niin mallinnus antaa isännän kulkemaksi matkaksi 66,7 m ja koiran 133,3 m, siis yhtäpitävästi edellä mainitun analyyttisen ratkaisun kanssa.
Kilpikonnagrafiikkamallia käyttäen tehtävä olisi laajennettavissa kokonaiseksi tehtäväkentäksi. Voidaan tarkastella koiran vauhdin (kuva 3) tai lähtöpaikan (kuva 4) vaikutusta sen kulkeman matkan pituuteen ja radan muotoon.
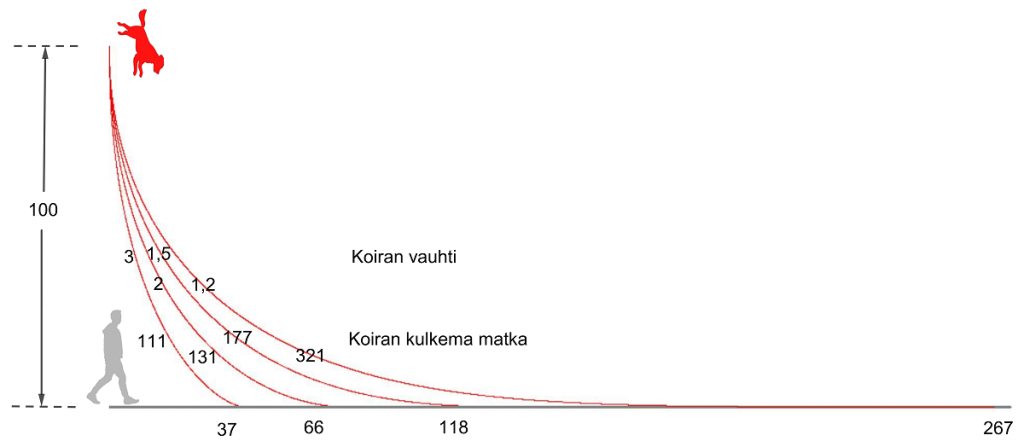
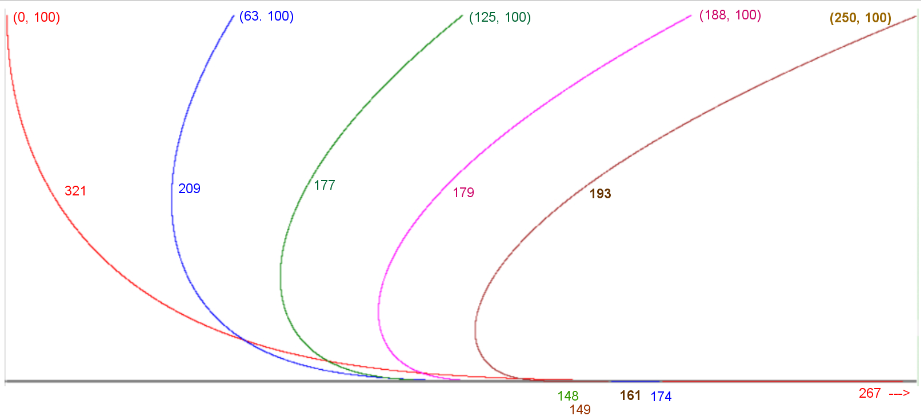
Pääsykoetehtävä vuodelta 1869
Markus Juhani julkaisi 4.6.2021 Facebook-ryhmässä Rakastan matematiikkaa tehtävän (kuva), jonka hän sanoi olleen MIT:n pääsykoetehtävänä vuonna 1869. Nykyään tehtävä näyttää niin tavanomaiselta yhdenmuotoisuustehtävältä, että peruskoululaisenkin pitäisi osata se.
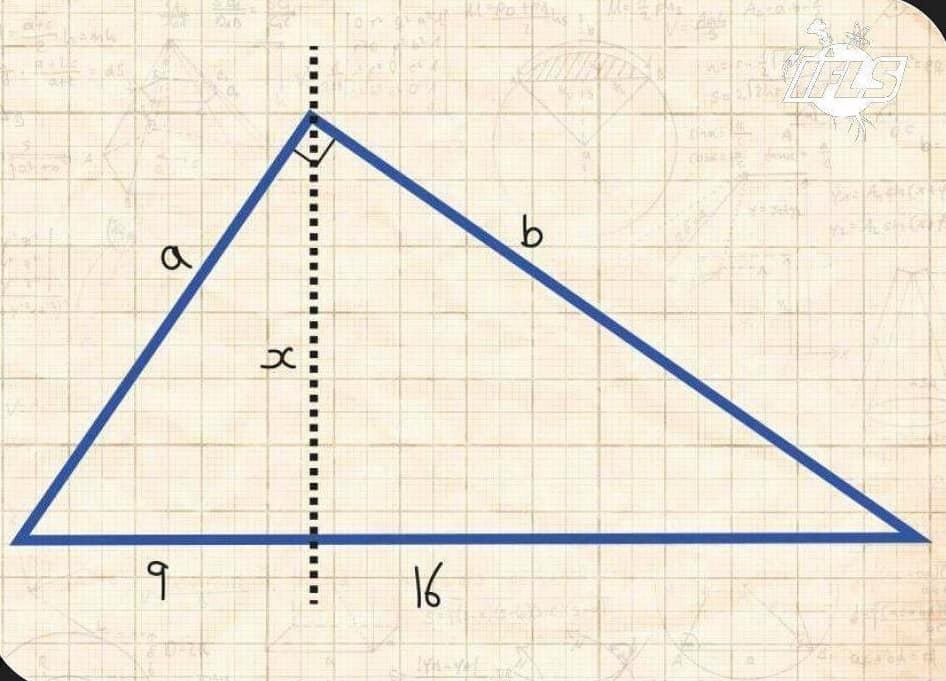
Tehtävää pidettiin hyvänä, jopa erinomaisena. Joku sanoi osaavansa ulkomuistista tämän kolmion sivujen pituudet. Muistipa joku muu vanhan koulugeometrian lauseen, jonka mukaan hypotenuusalle piirretty korkeusjana on hypotenuusan osien keskiverto eli geometrinen keskiarvo.







