Riemua matematiikasta

Matematiikasta irtoaa monenlaista mielihyvää. Koulussa se syntyy monesti oppimisen ja opetuksen onnistuneesta yhteisvaikutuksesta. Varga–Neményi-yhdistyksen toiminnanjohtaja Anni Lampinen on kiteyttänyt sen sähköpostimottoonsa näin: ”Opettajan suurin taito on herättää oivaltamisen ja oppimisen riemua!” Opettajan itsensäkin olisi hyvä opetella keksimään itselleen ilonaiheita opettamastaan asiasta. Riemua voi syntyä myös rajojen ylittämisestä.

Artikkeli perustuu Tartossa vuonna 2011 pitämäni esitelmän ”Rõõm matemaatikas” ideoihin.

Mistä siis matematiikan riemu voisi syntyä? Mitä se voisi olla? Onnistumista tehtävien ratkaisemisessa. Uuden asian ymmärtämistä. Yllättävän ratkaisun tai todistuksen keksimistä. Uuden idean löytämistä. Kauniisti visualisoitua matematiikkaa. Vakuuttavien perustelujen tai selitysten muotoilua. Omasta työstä saatua kannustavaa palautetta. Metkaa matematiikkaa (engl. recreational mathematics, ransk. mathématiques récréatives). 

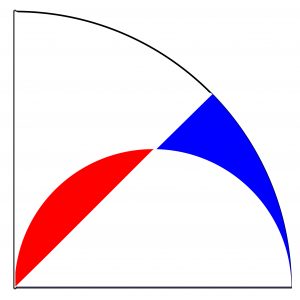
Ilon ja riemun suurin lähde on tekemisessä, onnistumisessa ja yllätyksissä. Eikä tehtävän tarvitse niin kummoinen olla eikä uusikaan muille kuin ratkaisijalleen. Niinkin vanhan tehtävän kuin Apollonioksen ongelman ratkaisujen piirtäminen voi ilahduttaa, jos löytää kolmen ympyrän tapauksen kaikki kahdeksan erilaista tilannetta [1]. Samoin niin yksinkertainen asia, että pystyy vertaamaan toisiinsa kuvan 1 punaista ja sinistä kuviota.

Itseäni kovasti ilahduttaneita keksintöjä ovat olleet tietokoneavusteisen algebran ja dynaamisen geometrian ohjelmat. Ne ovat nykyään arkipäivän työvälineitä koululaisellekin, mutta silloin, kun staattiset harppi- ja viivainkuviot alkoivat vähitellen elää mielessäni, koin monia riemullisia hetkiä. [3] Tuttukin alkeisgeometrian kuvio saa uutta viehätystä liikkeestä, kuten Pythagoraan lause nimimerkki Slikin animaatiossa Geogebran materiaaleissa [4].

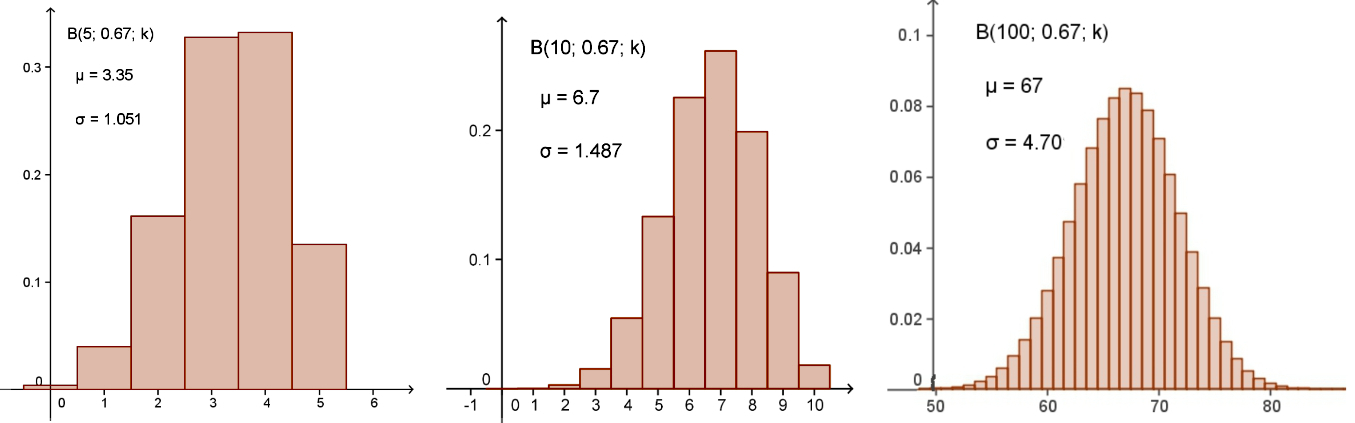
Ihan uusi ja ihastuttava idea minulle oli, että myös binomijakauma voi olla dynaaminen [5]. Esimerkiksi nastanheittoa (p = 0,67) voi simuloida vain säätämällä heittojen määrää. Samasta mallista saa myös rahanheiton (p = 0,5).

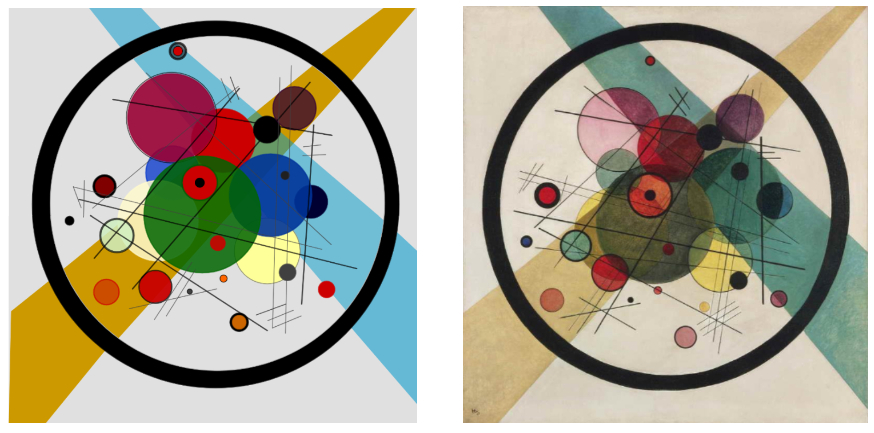
Visuaalisia elämyksiä saadaan aikaan myös siirtymällä matematiikan ja taiteen välisen rajan yli, esimerkiksi jäljittelemällä Vasarelyn tai Kandinskyn [6] töitä. Jos käytössä on dynaaminen matematiikkaohjelma, niin tuloksena voi olla muokattava ”aktiivitaulu”, josta voidaan piilottaa joitakin objekteja tai vaihtaa väriä kuvioon muuten koskematta. 

Rajoja voidaan ylittää matematiikasta myös runouden suuntaan. Lordi Byron on sanonut, että ”I know that two and two make four – –  if – – I could convert 2 and 2 into five it would give me much greater pleasure.” Ilmaisussa näkyy runoilijan eikä matemaatikon sielu. Runous ja matematiikka yhdistyivät sen sijaan esimerkiksi Omar Khaijamissa (1048–1131).

Meidän matemaatikkorunoilijamme on Aatos Lahtinen. Käänsin hänen runonsa Neliöjuuri viroksi ja esitin sen Tartossa vuonna 2011 [8]: 

Ehkä tämä muistelmapala on jo kovin kaukana matematiikasta, mutta se on kuvaava esimerkki siitä, mitä matematiikan opettajana tarkoitan rajojen ylittämisellä.

Lähteitä ja lisää luettavaa:

[1] Korhonen, Hannu: Kolme näkökulmaa Apollonioksen ongelmaan. Dimensio 2/2010 s. 52–53.

[2] Courant, T. Equal Regions Surprise. Geogebra-materiaali https://www.geogebra.org/m/djHuxKnv, viitattu 8.2.2018.

[3] Korhonen, H. Mielikuvat ja dynaamisuuden lumo. Dimensio 1/2009.

[4] Slik. An animated demonstration of the Pythagorean theorem. saatavissa osoitteesta https://www.geogebra.org/m/t5KDeERz, viitattu 8.2.2018.  Ei ole enää verkossa 2021. Sen sijaan siellä on esimerkiksi https://www.geogebra.org/m/YgHjzC5D (H Heinrichs).

[5] Koudounas, Constantinos: Binomial Distribution osoitteessa https://www.geogebra.org/m/FyMaDJgA, viitattu 6.5.2021.

[6] Esimerkiksi Geogebra-materiaali Kandinsky Generator https://www.geogebra.org/m/dkFdkjgq

[7] Robredo, Beatriz: Kandinsky – Círculos en un círculo osoitteessa https://www.geogebra.org/m/pca5uvgs

[8] Lahtinen, Aatos: Todellisuuden neliöjuuri. Mediapinta 2010. Esittely Dimensiossa 1/2011 s. 62–63.