Esivanhempien matematiikkaa
Sukupuut kertovat esivanhemmistamme. Kannamme soluissamme heidän perimäainestaan. Sen varassa on mahdollista ja mielekästä hahmotella sukupuita paljon muistitietoa ja kirjallista henkilökirjanpitoa kauemmaksi. Siinä matematiikka voi tulla avuksi.
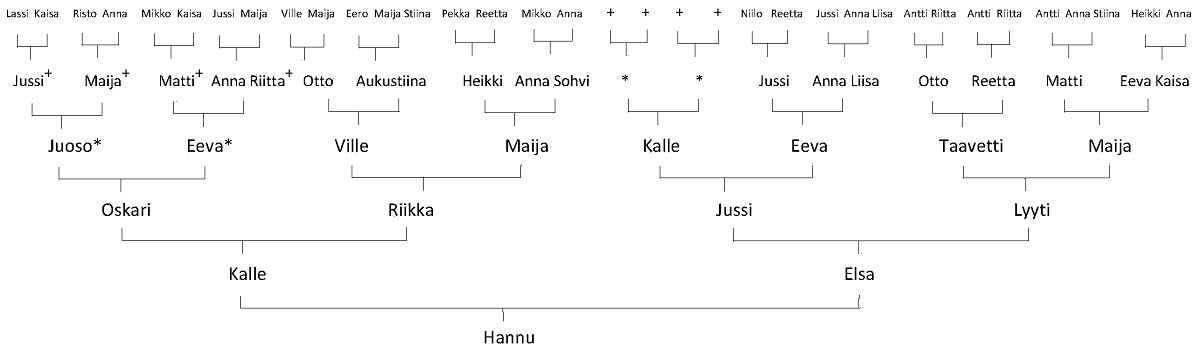
Jokaisella meistä on kaksi biologista vanhempaa, heillä kummallakin samoin kaksi. Siten meillä on neljä toisen polven esivanhempaa, kahdeksan kolmannen polven esivanhempaa (kuva 1) jne. Esivanhempien määrä näyttäisi siis kasvavan rajatta, mitä kauemmaksi taaksepäin mennään ajassa. Tämä on kuitenkin mahdotonta.
Maailman väestö oli pitkään suhteellisen pieni. Se alkoi kasvaa voimakkaasti vasta, kun teollinen saippuanvalmistus ja rokotukset alkoivat 1700-luvulla. Suomen alueella arvioidaan olleen uuden ajan alkaessa noin 300 000 ihmistä. Jos pidetään sukupolven pituutena lähimpien vuosisatojen väestötilastoihin perustuvaa keskimääräistä noin 30:tä vuotta, niin esivanhempien laskennallinen määrä ylittäisi koko väestömäärän jo keskiajan lopulla (kuva 2). Arvio on tietysti karkea, sillä keskiajalta ei ole mitään väestötilastoja. Tässä olen arvioinut väestömäärän pysytelleen pitkään suunnilleen samansuuruisena. Väestönkasvu on kyllä eksponentiaalista myös ennen vuotta 1750, mutta niin hidasta, että se ei näy kovin hyvin kuvan 2 mittakaavassa.
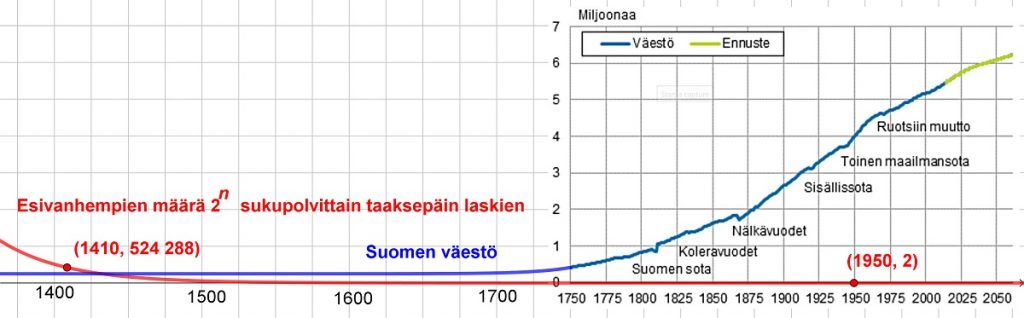
Suomen väestöön vertaaminen on perusteltua, sillä dna-analyysien perusteella perimäni on sataprosenttisesti suomalaista. Eikä periaate muutu, vaikka verrattaisiin esivanhempien määrää koko maapallon väestöön. Laskennallinen esivanhempien määrä ylittäisi kyllä senkin ennen pitkää, vajaassa tuhannessa vuodessa. Suomalaisten määrä antaa vain karkean ylärajan. Todellisuudessa esivanhempieni laskennallinen määrä ylittäisi todellisen vertailumäärän paljon nopeammin, sillä valtaosa esivanhempieni suvuista on pienestä, yhtenäisestä itäsuomalaisten populaatiosta, joka eroaa perimältään länsisuomalaisista yhtä paljon kuin nämä ruotsalaisista (kuva 3).
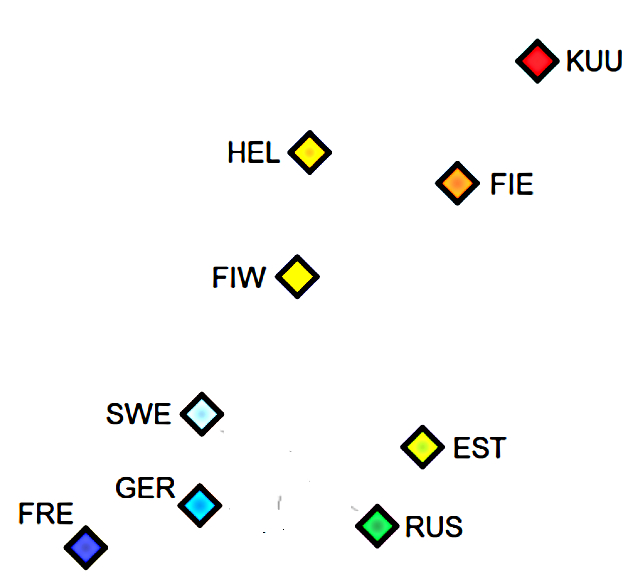
Viimeisten vuosisatojen suhteellinen kasvunopeus on ollut koko maapallolla suurempaa kuin Suomessa ja väestökasvu alkoi kiihtyä kolmisen sataa vuotta aikaisemmin [3] kuin Suomessa (kuva 4).
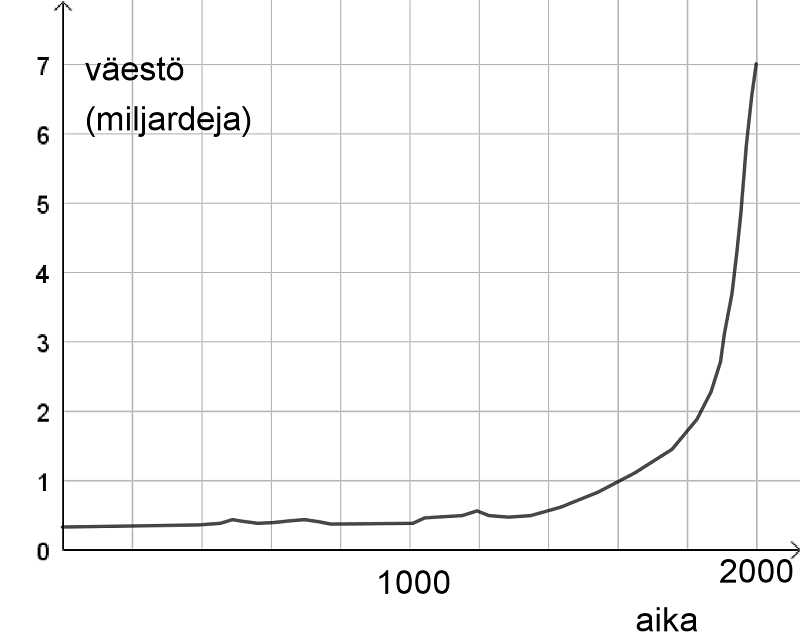
Mikä esivanhempien määrän laskemisessa on siis vikana? Se, että esivanhemmat ovat esivanhempia monia eri sukulaisuuslinjoja pitkin. Pitkällä aikavälillä nämä haaroittuvat ja yhtyvät enemmän verkkoa kuin puuta muistuttavaksi rakenteeksi. Esimerkki tästä omien esivanhempieni kohdalla näkyy jo kuvassa 1. Kaksi neljännen polven esivanhempaani (merkitty *:llä kuvassa 1) esiintyy nimittäin kaaviossa jo aikaisemmin kolmannessa esivanhempien polvessa. Viidennen polven esivanhemmista ”puuttuu” siis jo neljä (merkitty +:lla kuvassa 1). He ovat kaavion neljännen polven esivanhempien rivin vasemmassa laidassa. Aukko laajenee polvi polvelta. Viidennen polven esivanhemmissani on lisäksi ainakin kaksi, jotka aiheuttavat vastaavan esivanhempien kadon seuraaviin sukupolviin. Ja vielä vanhemmissa sukupolvissa, jotka tunnetaan kirjallisten lähteiden perusteella, on useita muita tällaisia aukkoja.
Tilastotieteen kieltä käyttäen kyse on siitä, että populaatiomallit eivät voi perustua tasaisiin jakaumiin, koska puolison valinta ei ole satunnaista [4]. Väestömallien rakentaminen on helppoa, jos oletetaan, että puolison valinta on ollut satunnaista (engl. random mating). Se ei kuitenkaan vastaa todellisuutta. Puolison valinta on ja on aikaisemmin ollut vielä selvemmin hyvinkin monimutkainen maantieteestä, kansallisuudesta, väestöryhmistä, kielestä, uskonnosta ja sosiaalisesta asemasta riippuva prosessi. Itäsuomalaisten esivanhempieni kohdalla maantiede ja sosiaalinen asema ovat ehkä olleet tärkeimmät tekijät, sillä puoliso on saatu useimmiten läheltä omasta tai naapurikylästä ja samalta sosiaaliselta tasolta.
Ei-satunnaisella puolisonvalinnalla (engl. non-random mating) on merkitystä useammallakin tavalla. Vastaavalla tavalla kuin päätellään, että on useita ihmisiä, jopa suomalaisia, joilla on täsmälleen sama määrä hiuksia, on päätelty virheellisesti, että esimerkiksi Kaarle Suuren (n. 745–814) täytyy olla kaikkien nykyisten eurooppalaisten esi-isä. Hänen aikaansa on nykyajasta noin 40 sukupolvea. Nykyään elävällä ihmisellä olisi runsaan tuhannen vuoden takana siis muodollisesti laskien $2^{40}$ eli noin biljoona esivanhempaa. Sehän on mahdotonta! Jossakin vaiheessa laskennallinen esivanhempien määrä olisi ollut yhtä suuri kuin kaikkien eurooppalaisten, jopa maailman kaikkien ihmisten määrä. Siis jokin heistä olisi välttämättä Kaarle Suuren jälkeläinen.
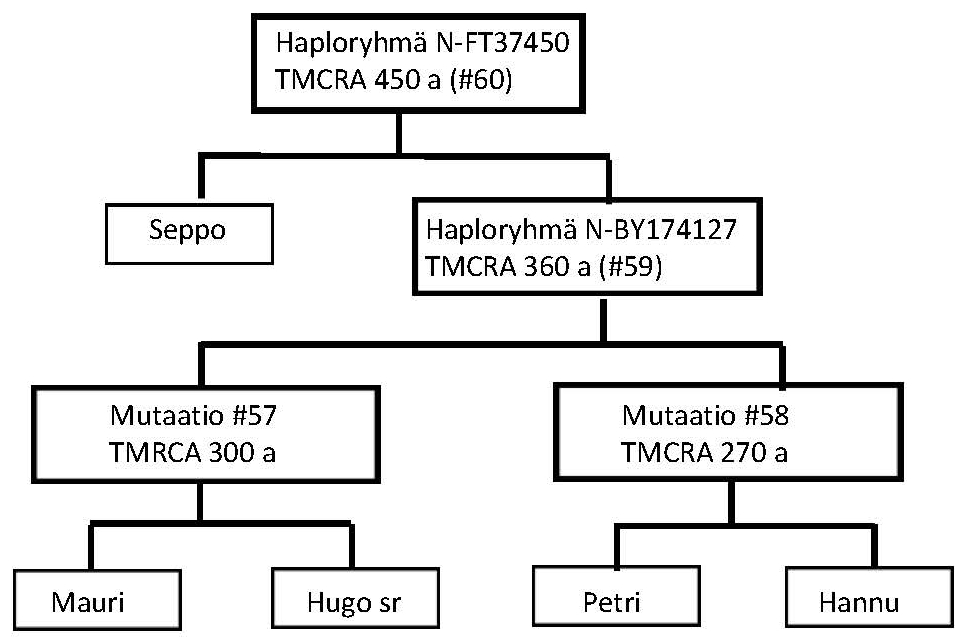
Todellista merkitystä ei-satunnaisella puolisonvalinnalla on geneettistä sukulaisuutta kuvaavien polveutumiskaavioiden eli ns. haplopuiden [5] solmukohtien eli uusien mutaatioiden syntymäajan arvioinnissa. Aika ilmoitetaan usein nuorimman yhteisen esivanhemman elinaikana (engl. time to most recent common ancestor TMCRA) (kuva5). Ääriesimerkki ei-satunnaisuudesta ovat täysin erityksissä eläneet ihmisryhmät, esimerkiksi Australian aboriginaalit, jotka elivät muusta ihmiskunnasta eristäytyneinä kymmeniä tuhansia vuosia. Itäsuomalaisten kohdalla perimän yhtenäisyyden syynä on ehkä enemmänkin lähtöpopulaation pienuus kuin varsinainen eristyksissä eläminen.
Matemaattisia populaatiomalleja on sovellettu eläin- ja kasvipopulaatioihin jo pitkään [7]. Tieteenalan perustajana pidetään englantilaista Thomas Robert Malthusia (1766–1834). Ihmispopulaatioiden matemaattinen mallintaminen laajassa mitassa on sen sijaan varsin nuorta. Erityistä pontta se on saanut viimeisen neljännesvuosisadan aikana sitä mukaa kuin ihmisen perimää on selvitelty yhä tarkemmin. Esivanhempien määrän nopealla kasvulla on populaatiomallien mukaan esimerkiksi se seuraus, että valtaosa, joissakin malleissa jopa 60–80
Lähteitä ja lisää lukemista:
[1] Tilastokeskus: Väestönkehitys vuosina 1749-2050 sivulla https://www.stat.fi/org/tilastokeskus/vaestonkehitys.html
[2] Häkkinen, J. Suomalaisten geenihistoria osoitteessa http://www.elisanet.fi/alkupera/Suomalaisten_geenihistoria.pdf
[3] Estimated world population figures 10 000 BC–AD 2000 https://en.wikipedia.org/wiki/World_population#/media/File:Population_curve.svg
[4] Humphrys, M. Common ancestors of all humans (using mathematical models) osoitteessa https://humphrysfamilytree.com/ca.math.html
[5] Esimerkiksi Ihmisen haploryhmän tyyppi osoitteessa https://fi.wikipedia.org/wiki/Ihmisen_haploryhm%C3%A4n_tyyppi
[6] Yksinkertaistettu ja mukailtu Ahti Mustosen kaaviosta 17.11.2020 osoitteessa https://www.familytreedna.com/groups/korhonen/activity-feed
[7] Population dynamics/History osoitteessa https://en.wikipedia.org/wiki/Population_dynamics







