Tribonaccin luvut ja sanat

Tunnet varmaan italialaisen 1200-luvun matemaatikon Fibonaccin ja hänen lukunsa. Mutta onko Tribonacci tuttu? Samasta maasta? Samalta vuosisadalta? Eipä vainkaan, vaan ajattomasta matematiikan ihmemaasta, missä kaikki on mahdollista ja aina voi itse keksiä lisää uutta.

Fibonaccin luvut rakennetaan rekursiivisesti laskemalla yhteen kaksi edellistä. Entä jos seuraava luku saataisiin laskemalla yhteen kolme edellistä? Tämän jonon ehdin jo nimetä mielessäni Tribonaccin luvuiksi ja luulin tehneeni suurenkin keksinnön, kunnes googletin hakusanalla ”tribonacci”. Tuli runsaat 200 000 tulosta. Haku ”tribonacci number” antaa sekin 12 000 tulosta. Enpä siis ollut mitenkään ensimmäinen. Silti niiden tutkimisessa riitti puuhaa ja haastetta.

Tribonaccin lukujonon siemenluvuiksi, siis kolmeksi ensimmäiseksi, on tarjolla useita vaihtoehtoja [1]. Seuraava luku saadaan aina rekursiivisesti kolmesta edellisestä. Jos aloitetaan luvuista 0, 0 ja 1, niin Tribonaccin jonon jäsenten kasvu on hyvin samantapaista kuin Fibonaccinkin jonon. Edellisen jonon kahdeksan ensimmäistä lukua ovat 0, 0, 1, 1, 2, 4, 7, 13 (kuva 1, toinen sarake vasemmalta) ja jälkimmäisen 0, 1, 1, 2, 3, 5, 8, 13. Sitten Tribonacci alkaa hiipiä edelle yhä nopeammin: kymmenes luku on 44 (34), kahdeskymmenes 19 513 (4 181), kolmaskymmenes 8 646 064 (514 229).

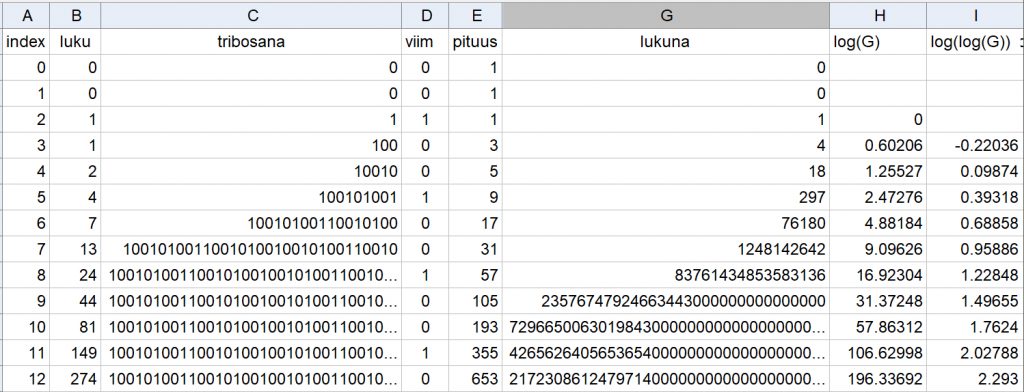
Myös Tribonaccin sanoista on kirjoitettu jonkin verran. Haku antaa englanniksi 2 600 tulosta, mutta ranskaksi tai suomeksi vain 1. Määrittelyt ja siemenjonot vaihtelevat sanojenkin osalta [2]. Yhteistä niille on se, että kolme ensimmäistä jäsentä annetaan ja seuraava saadaan aina kolmen edellisen avulla kirjoittamalla ne peräkkäin yhdeksi merkkijonoksi, viimeinen ensin. Käytän tässä jonoa, jonka jäseniä voisi kutsua binaarisiksi Tribonaccin sanoiksi, koska siemenmerkkeinä on vain nollia ja ykkösiä (kuva1, kolmas sarake vasemmalta).

Tribonaccin sanojen pituuden kasvu on aivan aluksi vähän hitaampaa kuin Fibonaccin sanojen [3], mutta jo kymmenes Tribonaccin sana on binaarimuodossa 105 merkkiä pitkä, kun vastaavan Fibonaccin sanan pituus on vain 55. Jos tarkastellaan tribosanoja lukuina, niin kasvu on samalla tavalla kaksoiseksponentiaalista (double exponential) kuin fibosanojenkin (kuva 2), kantaluku vähän suurempi kuin kultaisen leikkauksen suhde, noin 1,694.

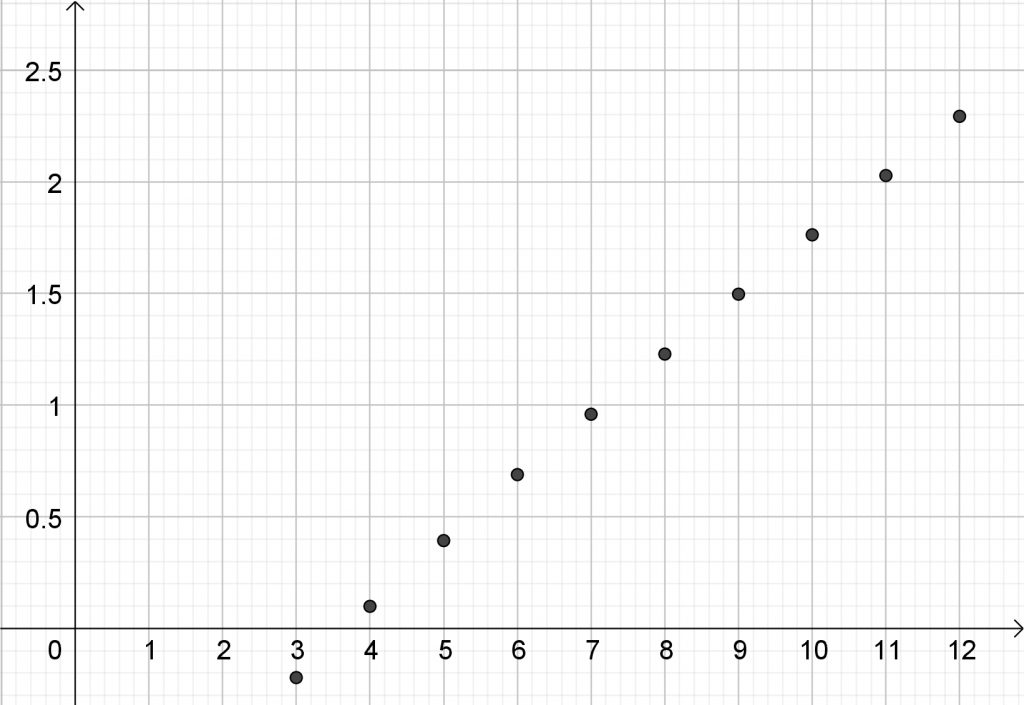
Tribonacci ei suinkaan ole Fibonaccin lisäksi ainoa, joka on kehitellyt omat lukunsa. On nimittäin olemassa Tetranacci (96 000 hakutulosta), Pentanacci (3 700), Hexanacci (3 000) (englanniksi myös esanacci), Heptanacci (2 900) jne. Niihin liittyvää matematiikka löydät verkkoartikkeleista, esimerkiksi [4], [5], [6], [7] ja lukujonojen verkkosanakirjasta OEIS [8] hakemalla nimellä.

Jos kukin lukujono aloitetaan nollilla niin, että ensimmäinen nollasta poikkeava luku on 1 nimeen sisältyvän järjestysluvun mukaisessa kohdassa ja seuraava luku saadaan aina laskemalla yhteen nimen mukainen määrä jonon edellisiä jäseniä, niin saadaan seuraavaa, kun jätetään alkunollat kirjoittamatta:

fibonacci       1    1    2    3    5      8     13     21       34        55        89        144        233        377        610       …

tribonacci      1    1    2    4    7    13     24     44       81      149      274        504        927      1705      3136       …

tetranacci     1    1    2    4    8    15     29     56     108      208      401        773      1490      2872      5536       …

pentanacci   1    1    2    4    8    16     31     61     120      236      464        912      1793      3525      6930       …

heksanacci   1    1    2    4    8    16     32     63     125      248      492        976      1936      3840      7617       …

heptanacci   1    1    2    4    8    16     32     64     127      253      504      1004      2000      3984      7936       …

Kullakin jonolla on omat ominaisuutensa, joista kaikki eivät näy helposti päällepäin. Niinpä esimerkiksi Fibonaccin lukujonon peräkkäisen jäsenten suhde lähestyy kultaista lukua

$\varphi=\frac{1+\sqrt{5}}{2}\approx1{,}618$

sitä tarkemmin, mitä pitemmälle jonossa edetään. Muillakin polynaccijonoilla on vastaava ominaisuus. Tribonaccin jonon vastaava raja-arvo Tribonaccin vakio on

$\frac{1+\sqrt[3]{19+3\sqrt{33}}+\sqrt[3]{19-3\sqrt{33}}}{3}\approx1{,}839$.

Lausekkeen monimutkaisuudesta huolimatta sillä on geometrinenkin sovellus tynkäkuution (snub cube) tilavuuden laskemisessa. [9]

Polynaccijonoja tutkitaan aktiivisesti. Yhdeksästoista kansainvälinen Fibonaccin lukujen ja niiden sovellusten konferenssi pidettiin verkkokonferenssina vuoden 2020 heinäkuussa [10]. Sovellutuksista on myös kirjallisuutta [11]. Onpa olemassa Tribonaccin lukujen päiväkin 13.7. Päivämäärän valinnan perusteen pitäisi selvitä katsomalla jonoa edeltä. Jos ei, niin sitten lähteestä 9. Ja vielä kannattaa huomata, että polynaccijonot ovat innostaneet myös muusikoita [12].

Lähteitä ja lisää luettavaa: [1] Katso esimerkiksi Tribonacci Sequence Term osoitteesssa https://math.stackexchange.com/questions/2280243/tribonacci-sequence-term tai Tribonacci Sequence osoitteessa https://brilliant.org/wiki/tribonacci-sequence/ tai Tribonacci Numbers osoitteessa https://www.geeksforgeeks.org/tribonacci-numbers/ tai Tribonacci Number osoitteessa https://mathworld.wolfram.com/TribonacciNumber.html

[2] Katso esimerkiksi Tribonacci Word sivulla https://www.geeksforgeeks.org/tribonacci-word tai Singh, Mr. Quasiperiodicity in the Tribonacci Word sivulla https://hal.archives-ouvertes.fr/hal-02141636/document tai OEIS A080843

[3]    Katso esimerkiksi Korhonen, H. ja Rahikka, M. Fibonaccin sanoja, Dimensio, syyskuu 2020, osoitteessa https://www.dimensiolehti.fi/fibonaccin-sanoja/

[4] Tribonacci Constant osoitteessa https://mathworld.wolfram.com/TribonacciConstant.html

[5] Tetranacci Number osoitteessa https://mathworld.wolfram.com/TetranacciNumber.html

[6] Piezas, T.  A Tale of Four Constants osoitteessa https://sites.google.com/site/tpiezas/0012

[7] Feng, J.  More Identities On the Fibonacci Numbers osoitteessa https://www.researchgate.net/publication/236343468_More_Identities_On_The_Tribonacci_Numbers

[8] The On-Line Encyclopedia of Integer Sequences osoitteessa http://oeis.org

[9] Tribonacci Numbers Day sivulla  Odditudes and Weirdities osoitteessa https://odditudes-and-weirdities.tumblr.com/post/55353571069/tribonacci-numbers-day-july-13

[10] The Nineteenth International Conference on Fibonacci Numbers and Their Applications osoitteessa http://pmf.unsa.ba/fibonacci19/index.php

[11] Bergum, G., Philippou, A. ja Horadam, A. Applications of Fibonacci Numbers, Springer 1988, osoitteessa https://link.springer.com/book/10.1007/978-94-009-1910-5

[12] Polynacci Sequence mathmetal osoitteessa https://soundcloud.com/thatonefella/polynacci-sequence