Perushahmotusta neljännen ulottuvuuden mieltämiseen, osa 2 – Kahdesta ulottuvuudesta kolmanteen
Ympäristömme on kolmiulotteinen. Meidän on lähes mahdotonta yrittää kuvitella neliulotteista tilaa, edes yksikertaisimpia neliulotteisia kappaleita. Kaksiulotteisen maailman tarkastelu on helpompaa. Jos yritämme ensin kuvitella omaa maailmaamme kaksiulotteisten eliöiden silmin, niin samantapaiset ajattelutavat saattaisivat auttaa meitä kurkistamaan myöhemmin neliulotteisiin maailmoihin.
Tunnetuin kaksiulotteinen maailma on varmaankin englantilaisen Edwin Abbott Abbottin luoma Flatland [1]. Sitä nimitettiin Pintalaksi Funktio-lehden sarjassa Ajan ja avaruuden geometriaa [2] 1980-luvulla. Käytän sen artikkelin suomenkielistä sanastoa seuraavassa, vaikka Abbottin kirja on myöhemmin suomennettu eri nimellä [3].
Abbottilla saattoi olla kirjaa kirjoittaessaan muitakin motiiveja kuin matematiikka. Kirja voidaan tulkita myös yhteiskuntakritiikiksi, sillä Pintalan yhteiskunta oli hyvin vahvasti luokkayhteiskunta. Asukkaat olivat monikulmioita ja sitä korkeammalla yhteiskuntahierarkiassa, mitä useampia kulmia heillä oli. Kertoja N. Eliö (alkuperäisteksissä A Square) oli siis varsin alhaisessa asemassa. Hänellä oli ulkoreunassaan silmä, jolla hän näki vain tason suuntaan.
Abbottin kirja ei saavuttanut aluksi suurta menestystä [4] , kunnes vasta seuraavan vuosisadan puolella 1920-luvulla, kun suhteellisuusteorian esittämiseen oli tarvittu neliulotteista koordinaatistoa, heräsi moniulotteisiin avaruuksiin kohdistuva kiinnostus. Lähes kulttimaineeseen Flatland kohosi 1900-luvun loppupuolella. Abbottin ideoita kehitettiin edelleen kirjan muodossa tasan sata vuotta myöhemmin [5]. Tehtiinpä aiheesta elokuva vielä tällä vuosituhannella [6]. Nimi esiintyy nykyään monessa muussakin yhteydessä populaarimusiikista pyöräilyyn.
Tässä yhteydessä meille on apua siitä, miten kolmiulotteisen avaruuden herra Pallo yritti selittää N. Eliölle omaa avaruudenkäsitystään. Jos Pallo oli kokonaan Pintalan ulkopuolella, niin N. Eliö ei voinut tietenkään nähdä sitä ollenkaan. Kun Pallo kulki Pintalan läpi, niin N. Eliö näki jumalaisen pyöreän kuvion. Hyvin korkeassa yhteiskunnallisessa asemassa siis, koska ympyrä samastui monikulmioon, jolla on äärettömän monta kulmaa. Kummallista vain oli, että herra Pallon koko näytti muuttuvan [7].

Vielä kummallisempi on herra A. Neliö (A niin kuin avaruus). Vaikka hän väittää olevansa N. Eliön serkku, vieläpä kaksoisolento, niin N. Eliöstä hän näyttää neulalta [8], siis hyvin teräväkulmaiselta, mikä tarkoittaa alinta kastia Pintalan yhteiskunnassa.

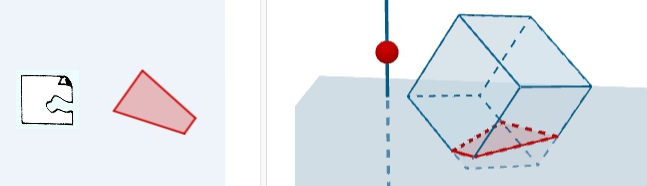
Eivätkä ihmeellisyydet tähän lopu. Kolmiulotteisessa avaruudessa Tilalassa (Avaruusmaa, Spaceland) asuu myös K. Uutio. Häntä ei ole Abbottin tai Ruckerin kirjassa, mutta joustava mieli voi hänetkin luoda [9].
Sarjan seuraavissa osissa tutustumme muihin keinoihin, joilla välittää tietoa kolmiulotteisesta avaruudesta kaksiulotteisille olioille. Ja vielä myöhemmin yrittää itse hahmottaa neliulotteisia kohteita näiden periaatteiden avulla.
Sarja jatkuu.
Sarjan aikasempi osa:
Perushahmotusta neljännen ulottuvuuden mieltämiseen, osa 1 – Mitä ne ulottuvuudet ovat? (25.3.2020)
[1] E. A. Abbott. Flatland, a Romance of Many Dimensions. Seeley & Co, Londin 1884.
Saatavissa esimerkiksi osoitteesta https://archive.org/details/flatlandromanceo00abbouoft/mode/2up
Hyvin monia muita painoksia, myös e-kirjana.
[2] Korhonen, H. Ajan ja avaruuden geometriaa 1: Neljäs ulottuvuus. Matemaattisten aineiden opettajien liiton koululaislehti Funktio 1980:2, s. 4–5, 7.
[3] Abbott, E. A. Tasomaa. Suom. Kimmo Pietiläinen. Terra Cognita 1991.
[4] Wikipedia-artikkeli Flatland osoitteessa https://en.wikipedia.org/wiki/Flatland.
[5] Rucker, R. The 4th Dimension. Toward a Geometry of Higher Reality. Hougjton–MIfflin, Boston 1984.
[6] Flatland , the Movie. Flat World Productions 2007.
Katso esimerkiksi https://en.wikipedia.org/wiki/Flatland:_The_Movie.
[7] Geogebra-matletti Flatland sphere 2 osoitteessa https://www.geogebra.org/m/xugpapz7
[8] Geogebra-matletti Flatland_square osoitteessa https://www.geogebra.org/m/rcsnabaz
[9] Christersson, M. Flatland. Geogebra-matletti osoitteessa https://www.geogebra.org/m/CrnH2mrY







