Na­vi­gaa­tio­fy­siik­kaa I – Va­lon ku­lun geo­met­riaa

Matematiikassa ja luonnontieteissä esimerkit arkielämästä motivoivat hyvin oppilaita. Vielä arkielämääkin paremmin toimivat esimerkit juhlasta. Ja mikä onkaan suurempaa juhlaa kuin purjehtiminen, mistä voi löytää hyviä esimerkkejä.

Navigaatiokirjallisuudessa, esim. [1], löytyy laskukaava etäisyyden laskemiseksi majakkaan, silloin kun majakan valo tulee juuri näkyviin horisontin takaa:

$s=2{,}08\left(\sqrt{\frac{H}{\mathrm{m}}}+\sqrt{\frac{h}{\mathrm{m}}}\right)\mathrm{M}$

(1)

jossa $H$ ja $h$ ovat majakan (valon) ja silmän korkeudet merenpinnasta. M = meripeninkulma (Nautical mile) = 1852 m. Herää kysymys, miten yllä oleva kaava on saatu.

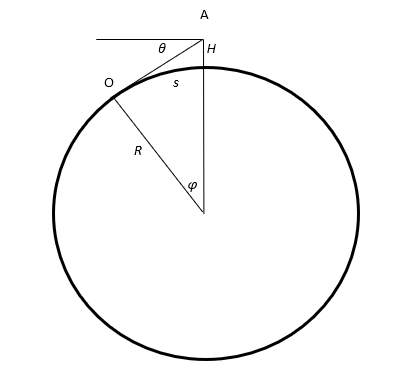
Tarkastellaan majakan korkeuden $H$ osuutta yhtälössä (1). Kuvassa 1. veneen asema on pisteessä O, majakan huippu pisteessä A. $R$ on maan säde. Etäisyys veneestä majakan juurelle isoympyrää pitkin on kaaren pituus $s$

$s\ =R\varphi=\ R\cos^{-1}\frac{R}{R+H}$

(2)

Olkoon

$y\ =\ \cos\varphi\ =\ \sqrt{1-\sin^2\varphi}$

(3)

eli

$\sin\varphi=\ \sqrt{1-y^2}$

(4)

Yhtälöissä (3) ja (4) on neliöjuuressa vain + merkki, koska kulma $\varphi$ on terävä. Nyt siis pätee

$\varphi=\ \cos^{-1}y=\ \sin^{-1}\sqrt{1-y^2}$

(5)

Yhtälö (2) voidaan siten kirjoittaa

$s\ =R\ \sin^{-1}\sqrt{1-\left(\frac{R}{R+H}\right)^2}=R\ \sin^{-1}\frac{\sqrt{2RH+H^2}}{R+H}$

(6)

Jatkuvasti derivoituva funktio $f(x)$ voidaan lausua (sarjan suppenemisalueella) origon ympäristössä MacLaurinin sarjana (erikoistapaus yleisemmästä Taylorin sarjasta).

$f(x)=\ f(0)+f'(0)x+\ \frac{1}{2!}\ f”(0)x^2+\ \cdots$

(7)

Lausutaan yhtälössä (6) arcsin-funktio tämän mukaisesti MacLaurinin sarjana ja otetaan siitä kaksi ensimmäistä termiä. (Huomaa, että koska arcsin-funktio on pariton funktio, niin vain parittomien potenssien termit ovat nollasta poikkeavia funktion MacLaurinin sarjassa.)

$s\ \cong R\left(\frac{\sqrt{2RH+H^2}}{R+H}\ +\ \frac{1}{6}\ \left(\frac{\sqrt{2RH+H^2}}{R+H}\right)^3+\ldots\right)$

(8)

Kehitetään tämä edelleen potenssisarjaksi korkeuden $H$ mukaan:

$s=\ \sqrt{2RH}\ \cdot\ \left(1-\ \frac{5}{12}\cdot\frac{H}{R}+\ldots\right)$

(9)

Ensimmäinen korjaustermi on enimmilläänkin vain joitakin sadastuhannesosia ja voidaan siten unohtaa. Siten saadaan

$s=\ \sqrt{2RH}$

(10)

Samaan tulokseen päätyy myös laskemalla suoraa näköetäisyyttä majakan huippuun Pythagoraan lauseesta.

$s=\ \sqrt{\left(R+H\right)^2-\ R^2}=\ \sqrt{2RH}\ \cdot\ \sqrt{1+\ \frac{H}{2R}}$

(11)

Kehitetään neliöjuurilauseke yhtälössä (11) taas MacLaurinin sarjaksi, jolloin saadaan

$s=\sqrt{2RH}\ \cdot\ \left(1+\ \frac{1}{4}\cdot\frac{H}{R}+\ldots\right)\ \cong\ \sqrt{2RH}$

(12)

Ensimmäisen korjaustermin kertoimen erilaisuus yhtälöissä (9) ja (12) kuvaa eroa etäisyyksissä mitattuna toisaalta isoympyrää pitkin majakan juurelle ja toisaalta viivasuoraan majakan huippuun.

Nyt meripeninkulman (alkuperäisen) määritelmän perusteella

$R=\frac{360\cdot60\ \mathrm{M}}{2\pi}$

(13)

jolloin etäisyydeksi saadaan (majakan osuus)

$s=\ \sqrt{\frac{2\cdot360\cdot60\ \mathrm{M}}{2\pi}\ \cdot\frac{H}{1852\ \mathrm{m}}\ \mathrm{M}}=\ \sqrt{\frac{360\cdot60}{1852\ \pi}\ }\cdot\ \sqrt{\frac{H}{\mathrm{m}}}\ \mathrm{M}=1{,}927\ \mathrm{M}\sqrt{\frac{H}{\mathrm{m}}}$

(14)

Tämä geometrinen tulos poikkeaa yhtälöstä (1) noin 8

Lähdeviitteet

[1] Suomen Navigaatioliitto: Veneilijän merenkulkuoppi II, Rannikko-navigointi, Unigrafia Oy, Helsinki, 2013

Aloituskuva Phot Daniel Kuruvilla on Unsplash