Rengasta täplä
Koulussa käytetään tavallisimmin kymmenjärjestelmää lukujen merkitsemiseen. Joskus saattaa vilahtaa esiin myös kaksijärjestelmä, varsinkin tietokoneista puhuttaessa. Mutta oletkos kuullut täpläjärjestelmästä?
Täpläjärjestelmässä [1] ei käytetä numeroita, vaan vain täpliä (pisteitä) ja renkaita (ympyröitä). Periaate on seuraava:
(1) yksittäinen täplä edustaa lukua 1
(2) rengastettu täplä edustaa lukua 2
(3) kahden renkaan sisällä oleva kaksinkertaistetaan kahteen kertaan ja niin edelleen jokaiselle renkaalle
(4) kussakin renkaassa saa olla enintään yksi täplä.
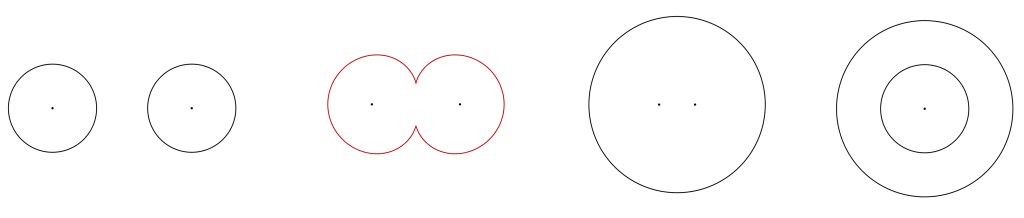
Lukujen merkitsemisessä ei siis käytetä numeroita, vaan vain pisteitä ja ympyröitä (kuva 1).

Miten merkitset luvun 8 täpläjärjestelmässä? Entä luvun 27? Entä luvun 0?
Yhteenlasku on täpläjärjestelmässä dynaaminen prosessi. Kaksi ykköstä lasketaan yhteen niin, että pisteet siirretään päällekkäin ja piirretään ympyrä sen ympärille merkiksi siitä, että niitä on kaksi. Kaksi kakkosta lasketaan yhteen siirtämällä renkaat lähemmäksi toisiaan niin, että kehät yhtyvät (kuva 2), sisällä olevat pisteet siirretään päällekkäin ja tämän merkiksi piirretään toinen, sisempi ympyrä. Sanoin selitettynä menettely (yhteenlaskualgoritmi!) kuulostaa ehkä monimutkaiselta, mutta dynaaminen matletti [2] selventää asiaa ja osoittaa, että menettely toimii suuremmillakin luvuilla.
Täpläjärjestelmän kertolasku taas puolestaan kuulostaa sanoin selitettynä paljon yksinkertaisemmalta kuin sen suoritus piirrettynä onkaan. Kerrottavan jokainen täplä korvataan kertojan kopiolla ja sitten yhdistetään renkaat niin, että lukumerkintä on sääntöjen (1)–(4) mukainen (kuva 3). Suorituksen voit nähdä matletista [3]. Tämä vastaa numeroin merkittyjen lukujen kertolaskualgoritmia, jossa kerrottavan kutakin lukuyksikköä osoittava luku kerrotaan vuorollaan kertojan kutakin lukuyksikköä osoittavalla luvulla.
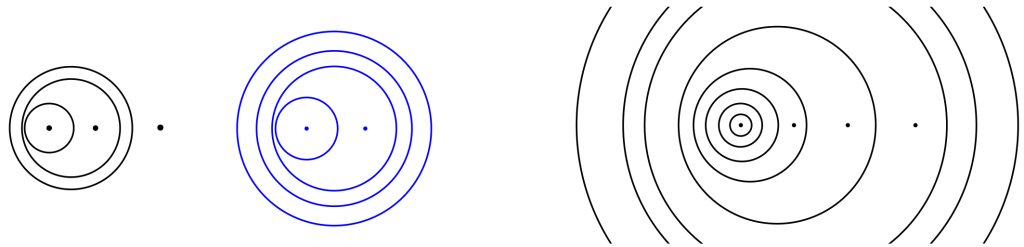
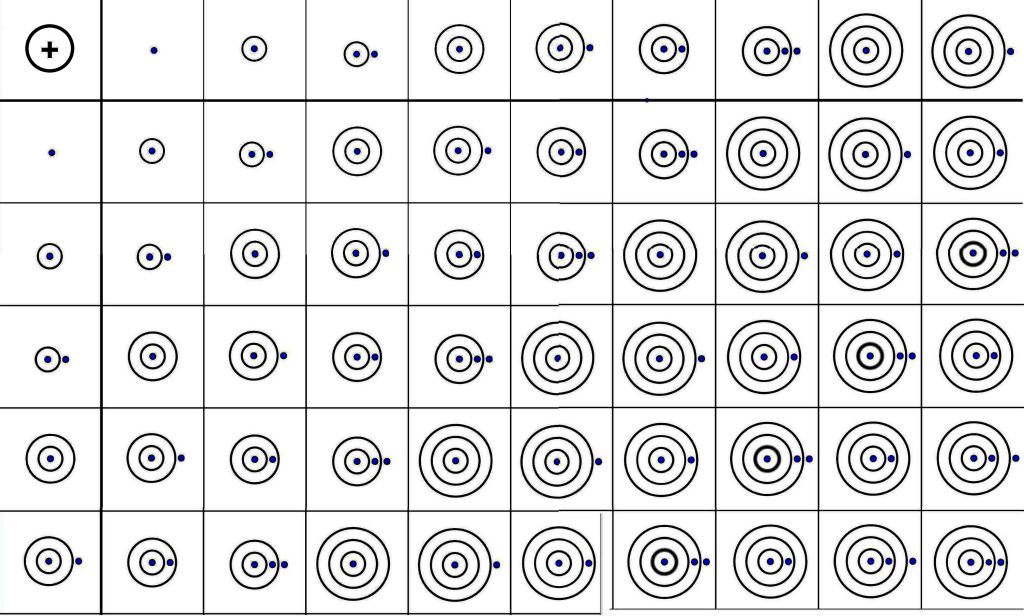
Täpläjärjestelmässä on vain yksi numero: täplä. Sen arvo riippuu siitä, kuinka monen ympyrän sisällä se on. Kaikkien ympyröiden ulkopuolella olevan täplän arvo on 1. Jokainen ympyrä kaksinkertaistaa sen arvon. Kyse on siis tavallaan graafisesta paikkajärjestelmästä. Yhteenlaskutaulu(ko)n (kuva 4) otsikkorivin oikeanpuolimmainen luku voitaisiin siis esittää muodoissa ●○○●, jos sovitaan, että oikeanpuolimmaisen täplän arvo on yksi ja siitä vasemmalle täplän arvo aina kaksinkertaistuu paikka paikalta. Tyhjä täplä ”○” merkitsee ympyrärengasta, jossa ei ole pistettä lainkaan. Tämähän on sama periaate, jota käytetään kaksijärjestelmässä:
10012 = 1 · 2³ + 0 · 2² + 0 · 2¹ + 1 · 2ᴼ.
Mielekkäästi voitaisiin keskustella siitä, mikä näistä kolmesta merkintätavasta – edellä oleva neljän täplän rivi, kaksijärjestelmän lukumerkintä vai täpläjärjestelmän kuva – esittää tarkoituksensa kaikkein tiiveimmin tai havainnollisimmin. Eri asia on sitten tietysti se, mikä niistä on kätevin laskemisen tai lukusanojen muodostamisen kannalta. Olisivatko lukusanat edes tarpeellisia, jos visuaalisesti kommunikoivien matemaatikoiden ajattelu perustuisi vain kuviin eikä sanoihin?
Täpläjärjestelmän yhteenlaskualgoritmi on nimittäin täysin graafinen, niin kuin edellä esitettiin, sitä vastoin, että numeeristen lukujärjestelmien algoritmit perustuvat symbolein (numeroin) merkittyjen lukujen manipulointiin. Ajattelutavan omaleimaisuutta ilmentää sekin, että toiminnot (operaatiot) voitaisiin nähdä analogisina yhteensulauttamisina ja moninkertaistamisina, ellei matematiikkamme (aritmetiikkamme) olisi totuttanut meitä ajattelemaan lukumäärinä miellettäviä kohteita koskevia operaatioita laskutoimituksina ja käyttämään niistä laskemiseen liittyviä mielleyhtymiä ja sanastoa.
Säännönmukaisuuksia
Täpläjärjestelmän lukuhamoista erottuvat helposti parilliset ja parittomat luvut. Jälkimmäisissä on kaikkien ympyröiden ulkopuolella täplä, parillisissa ei. Vastaavasti on helppo löytää ne luvut, joita me kutsumme kakkosen potensseiksi. Niissä on vain yksi täplä keskellä. Samoin näitä yhtä pienemmät luvut, ne joiden joukosta löytyvät Mersennen alkuluvut. Niissä on täplä jokaisessa renkaassa ja vielä renkaiden ulkopuolellakin.
Alkulukuja on yhtä vaikea etsiä täpläjärjestelmässä kuin kaksi- tai kymmenjärjestelmässä. Eratostheneen seula toimii sielläkin (kuva 5). Miltä kuulostaisivat täpläjärjestelmän jaollisuussäännöt esimerkiksi kolmella tai viidellä jaollisille luvuille?

Lähteitä ja lisää luettavaa
[1] Henle, Jim: Ring-a-Ding Numeration System osoitteessa https://www.science.smith.edu/~jhenle/Ringading/
[2] Ring-a-Ding Addition osoitteessa http://www.science.smith.edu/~jhenle/Ringading/addition.html
[3] Ring-a-Ding Multiplication osoitteessa http://www.science.smith.edu/~jhenle/Ringading/multiplication







