Alkuluvuista ja jaollisuudesta

Alkuluvut ovat lukuteorian ydintä, siis kovaa ja teoreettista matematiikkaa. Niillä on kuitenkin käyttöä niinkin kaukana koulumatematiikasta olevalla sovellusalueella kuin salakirjoituksissa. Kouluopetuksessa alkulukuja voitaisiin käsitellä paljon nykyistä enemmän, sillä niihin liittyy monenlaista lukukäsitteen rakentamiseen tähtäävää oppimista ja edelleen avoimia ongelmia. Perusasiat ovat tuttuja jokaiselle opettajalle. Tässä niitä on koottu kokonaisuudeksi, josta voit toivottavasti poimia yksittäisiä ajatuksia luokkaan vietäväksi, opetitpa sitten matematiikkaa alkuopetuksessa tai lukion pitkän matematiikan kursseilla.

Määritelmän mukaan alkuluku (engl. prime number, ransk. nombre premier) on luonnollinen luku, jota ei voida jakaa tasan millään muulla luonnollisella luvulla kuin ykkösellä ja itsellään, esimerkiksi 5, 11 ja 347. Siksi sanotaan, että alkuluvut ovat jaottomia. Luku 1 ei ole alkuluku, mutta luku 2 on.

Muut luonnolliset luvut kuin alkuluvut ja 1 voidaan jakaa tasan jollain muulla luonnollisella luvulla, esimerkiksi 12 : 2 = 6 ja 817 : 43 = 19. Niitä sanotaan jaollisiksi tai yhdistetyiksi. Ne voidaan esittää tulon muodossa, esimerkiksi 12 = 2 · 2 · 3 ja 817 = 19 · 43.

Hajotelmia ja tulomuotoja

Tarkastelemme ensin alkuluvun jakamista osiin. Mitä, eikö se olekaan yksi, yhtenäinen jakamaton kokonaisuus? On kyllä, kun puhutaan kertolaskusta, mutta yhteenlasku puree siihenkin. Pudotapa 11 hernettä hajotuskoneeseen [1] (kuva 1). Saat esimerkiksi summat

         4 + 7 tai 5 + 6 tai 8 + 3,  

tai

         2 + 4 + 5 tai 3 + 4 + 4

tai jopa

         1 + 3 + 3 + 4,

jos koneen syöttösuppilon alapäässä on monimutkaisempi seinämä, joka jakaa sen alan useampaan osaan. Jos sinulla ei hajotuskonetta ole, niin äkkiäkös sellaisen rakennat.

Kokeile muilla luvuilla. Millaiset lukumäärät herneitä hajotuskoneeseen pudotettuna voisivat antaa hajotelmia, joissa kaikki yhteenlaskettavat ovat yhtä suuria, esimerkiksi

         2 + 2 + 2 tai 5 + 5 + 5 + 5?

Tällaiset hajotelmat voidaan kirjoittaa lyhyemmin:

         3 · 2 tai 4 · 5.

Keksi lisää lukuja, jotka voidaan hajottaa yhtä suuriksi yhteenlaskettaviksi. Kirjoita ne sekä summina että tuloina.

Miten merkitset tulona lukua, jolla on hajotelma

         17 + 17 + … + 17 + 17

missä pisteiden paikalla on 33 lukua 17? Voidaan merkitä siis

         17 + 17 + … + 17 + 17 = 37 · 17 = 629.

Luku 629 ei ole alkuluku, vaan jaollinen luvuilla 17 ja 37. Juuri tämä jaollisuus erottaa alkuluvut muista luonnollisista luvuista.

Luonnollisia lukuja on äärettömän monta. Havaitset sen esimerkiksi siitä, että otatpa miten suuren luvun hyvänsä, niin aina voit tehdä suuremman lisäämällä lukuusi ykkösen. Suurten, monella tavalla jaollisten lukujen tekemiseen on erityinen keino: kertoma. Se tarkoittaa peräkkäisten luonnollisten lukujen tuloa ykkösestä alkaen. Sitä merkitään huutomerkillä, esimerkiksi 6! = 1 · 2 · 3 · 4 · 5 · 6 = 720. Kertomaa seuraavaa lukua, esimerkiksi 6! + 1 = 721, ei voida jakaa tasan millään luvuista 1, 2, 3, …, 6, sillä aina jää jakojäännökseksi 1. Se voi tietysti olla jaollinen jollakin suuremmalla luvulla, esimerkiksi 721 on jaollinen luvuilla 7 ja 103, siis 721 = 7 · 103.

Myös alkulukuja on äärettömän monta. Jos nimittäin olisi olemassa suurin alkuluku s, niin voidaan muodostaa luku, joka on yhtä suurempi kuin s:n ja sitä pienempien alkulukujen tulo. Merkitään sitä S:llä:

         S = 1 + 2 · 3 · 5 ·7 ·11 · … · s.                         

Se on luonnollisesti (paljon) suurempi kuin s. Jos S olisi alkuluku, niin s ei olisi ollutkaan suurin alkuluku, koska siis aina voitaisiin tehdä suurempi alkuluku kuin s. Jos taas S ei ole alkuluku, vaan jaollinen, niin pitää olla olemassa jokin s:ää suurempi alkuluku, sillä S ei ole jaollinen s:llä tai millään sitä pienemmällä alkuluvulla, koska niillä jaettaessa jää aina jakojäännökseksi 1. Ei siis voi olla olemassa suurinta alkulukua.

Alkuluvuista voidaan tehdä yhä suurempia alkulukuja. Esimerkiksi jotkut luvuista 2ⁿ – 1, missä n on alkuluku ja jotka saadaan siis vähentämällä ykkönen kakkosen potenssista, esimerkiksi

         2² – 1 = 3, 2³ – 1 = 7, 2⁵ – 1 = 31 ja 2⁷ – 1 = 127,

ovat alkulukuja (Mersennen alkuluku). Tätä muotoa on myös suurin toistaiseksi tunnettu alkuluku

         2^{82 589 933} – 1.

Siinä on lähes 25 miljoonaa numeroa [2].

Mielenkiintoinen on myös sellainen luonnollinen luku, joka voidaan esittää hajotelmana, jossa yhteenlaskettavina ovat vain lukua itseään pienemmät tekijät, esimerkiksi

         6 = 1 + 2 + 3 ja 28 = 1 + 2 + 4 + 7 + 14.

Tällaisesta luvusta käytetään nimitystä täydellinen luku (engl. perfect number). Niitä ovat esimerkiksi

         6, 28, 496, 8 128 ja 33 550 336.

Osaatko esittää viimeksi mainitun tulona ainakin muutamalla tavalla? Entä tekijöidensä summana edellä mainittuun tapaan (25 yhteenlaskettavaa!)? Ei tiedetä, onko parittomia täydellisiä lukuja olemassa. Ei myöskään sitä, onko täydellisiä lukuja ääretön määrä [3].

Jaollisuutta voidaan havainnollistaa suorakulmioluvuilla. Huomaa, että käytän terminologiaa, jonka mukaan Eulerin suorakulmioluvut (engl. pronic numbers), joiden sivut ovat peräkkäisiä kokonaislukuja, ovat vain suorakulmiolukujen erikoistapaus. Jaolliset luvut voidaan esittää suorakulmioina, joiden sivut ovat luvun tekijöitä. Yhdellä luvulla on sitä useampia suorakulmioesityksiä, mitä enemmän sillä on tekijöitä. Alkuluvuista ei voi tehdä suorakulmioita, vaan ne muodostavat vain yhden rivin (kuva 2).

Jaollisuus koulussa

Vanhastaan jaollisuutta on opetettu jaollisuussääntöjen avulla. Tavallisimmat niistä [4] ovat luvuille 2–5 ja 9, mutta niitä on kehitetty [5] ainakin luvuilla 2–30, esimerkiksi:

• ”Luku on kahdella jaollinen, jos sen viimeinen numero on 2, 4, 6, 8 tai 0.”
• ”Luku on kolmella jaollinen, jos sen numeroiden summa on kolmella jaollinen.”
• ”Luku on neljällä jaollinen, jos sen kahden viimeisen numeron muodostama luku on neljällä jaollinen.”
• ” Luku on yhdellätoista jaollinen, jos sen numeroista vuorotellen yhteen- ja vähennyslaskuilla saatu luku on yhdellätoista jaollinen.”

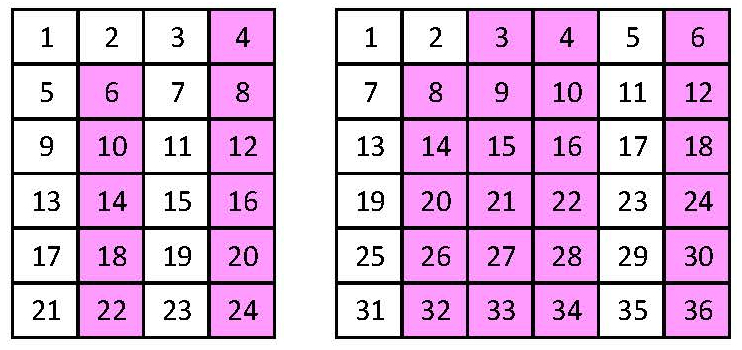
Varga–Neményi-menetelmän mukaisessa opetuksessa jaollisuuteen johdattelu alkaa jo alkuopetuksessa konkreettisesta ositusjaosta ja monikerroista [6]. Jaetaan 10 omenaa kolmelle lapselle. Ei mene tasan, vaan jää yksi yli. Mitkä olisivat sellaisia määriä, että jako menisi tasan? No, kolmen kerrannaiset – monikerrat – tietysti. Sitten pohditaan tilannetta muille lapsi- ja omenamäärille. Monikertoja opetellaan sujuvaksi taidoksi asti lukualueella 0–100 luettelemalla tasavälein rakentuvia (aritmeettisia) lukujonoja sekä kasvavaan että vähenevään suuntaan. Tuloksia kootaan monikertataulukoiksi niin, että ykkösnumero on sama kussakin sarakkeessa (kuva 3). Kolmosen monikertataulu poikkeaa muista, koska siinä esiintyvät kaikki numerot ykkösnumeroina.

Taulukoita tutkitaan monella tavalla ja etsitään kaikki säännönmukaisuudet. Samalla opetellaan niiden avulla päättelemään mistä tahansa lukualueen luvusta, onko se tietyn luvun monikerta eli jaollinen sillä. Haetaan helppoja ankkureita, esimerkiksi tasakymmeniä, ja muita monikertoja. Kolmosen monikertataulusta saadaan kuutosen monikerrat ottamalla joka toinen, yhdeksäisen monikerrat ottamalla joka kolmas jne. Jatketaan myös sarakkeisiin muodostuvia monikertajonoja, joissa vaihtuvatkin kymmennumerot. Monikertojen avulla opitaan tunnistamaan jaolliset luvut ilman, että jaollisuutta tarvitsee opettaa erillisenä asiana. Luvut tulevat tutuiksi, mikä myös vahvistaa lukukäsitettä.

Neljännellä luokalla voidaan etsiä monikertoja eli siis jaollisia lukuja satataulusta (-ruudukosta). Kun merkitään satatauluun 2:lla jaolliset luvut (joka toinen), 3:lla jaolliset (joka kolmas) jne., niin joihinkin ruutuihin kasautuu paljon merkintöjä. On siis toinen toistaan jaollisempia lukuja. Missä ruuduissa on eniten merkintöjä? Mikä on siis sataruudukon superjaollisin luku? Toisaalta on joitakin ruutuja, joihin ei tule mitään merkintöjä. Niissä majailevat alkuluvut. Ne voidaan siis löytää tarvitsematta laskea ensimmäistäkään jakolaskua. Luvut tulevat tutuiksi, mikä helpottaa sekä kerto- että jakolaskun oppimista myös niillä oppilailla, joille laskutoimitusalgoritmien muodollinen käsittely sääntöjen mukaan on työlästä.

Yläkoulussa jaollisuustietoja ja -taitoja tarvitaan erityisesti murtolukujen ja -lausekkeiden laskutoimitusten yhteydessä, muun muassa suurinta yhteistä tekijää ja pienintä yhteistä jaettavaa määritettäessä. Muuten alkulukujen opettaminen on opettajakohtaista yläkoulussa [7]. Lukiossa jaollisuus ja alkuluvut sisältyvät omana opetussuunnitelman perusteiden mukaisena jaksonaan lukion pitkän matematiikan kurssiin 11 [8], noin kolmannes kurssin tuntimäärästä. Koulukursseihin eivät sen sijaan kuulu esimerkiksi Wilsonin ja Leibnizin lauseet; edellinen mukaan positiivinen kokonaisluku n ≥ 2 on alkuluku, jos ja vain jos (n − 1)! antaa jakojäännökseksi luvun n −1 jaettaessa n:llä, sekä jälkimmäisen mukaan positiivinen kokonaisluku n ≥ 2 on alkuluku, jos ja vain jos (n − 2)! antaa jakojäännökseksi luvun 1 jaettaessa n:llä [9].

Alkulukujen etsiminen

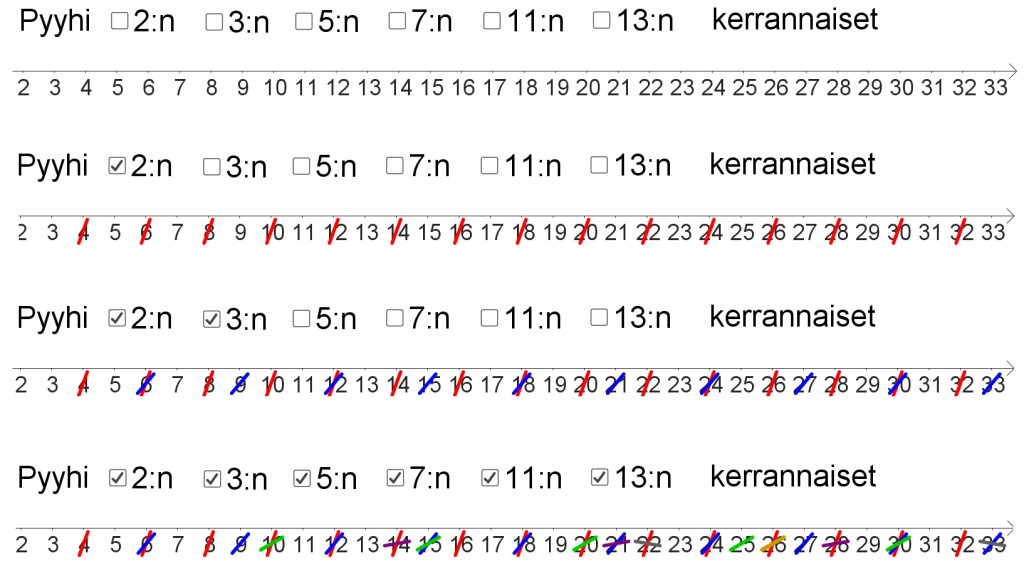
Mitään tapaa konstruoida alkulukuja tunnetuista alkuluvuista ei tunneta; siksi niitä on vain etsittävä positiivisten kokonaislukujen joukosta tai sen osajoukoista [10]. Vanhastaan tunnettu menetelmä on Eratostheneen seula [11]. Luonnollisten lukujen jonosta pyyhitään pois kakkosen kerrannaiset, sitten kolmosen kerrannaiset, viitosen kerrannaiset jne. Lopulta jäävät jäljelle jaottomat alkuluvut (kuva 4, alarivi). Tämä ideahan mainittiin jo edellä sataruudukon yhteydessä. Sitä voitaisiin käyttää alkuluvun operationaalisena määritelmänä:

alkuluvut ovat kokonaislukuja n, joilla ei ole muita, lukua $\sqrt{n}$ pienempiä tai sen kanssa yhtä suuria jakajia kuin 1.

Erityisen hyödyllisiä ovat jakojäännöksen näyttävät hajotelmat 4n + r ja 6n+r, missä n = 0, 1, 2, …. ja r = 0, 1, … , n–1. Kaikki parittomat alkuluvut ovat muotoa 4n + 1 tai 4n + 3, sillä muotoa 4n ja 4n + 2 ovat jaollisia kahdella (kuva 5, vasen). Parittomat alkuluvut ovat myös muotoa 6n+1 tai 6n+5, sillä muotoa 6n, 6n + 2 ja 6n + 4 ovat jaollisia kahdella ja muotoa 6n + 3 jaollisia kolmella (kuva 5, oikea). Usein merkitään myös muotoa 4n + 3 olevia lukuja lausekkeella 4n – 1 ja 6n + 5 olevia lukuja lausekkeella 6n – 1, mistä jakojäännös ei kuitenkaan näy samalla tavalla suoraan.

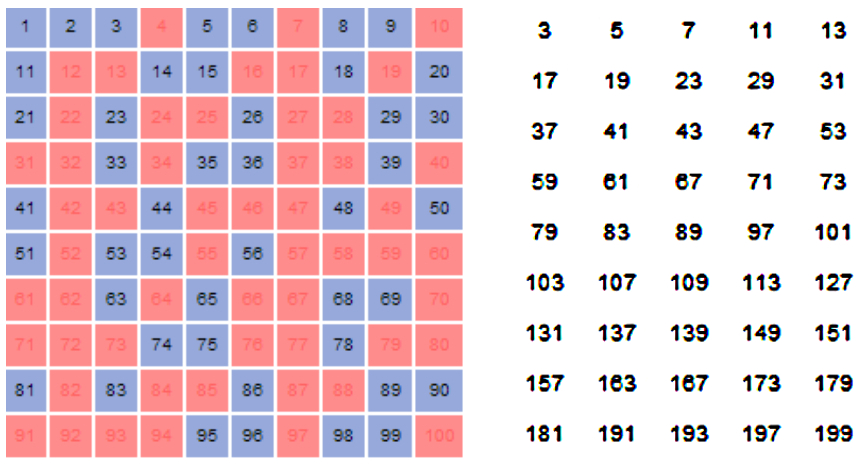
Sundaramin seula on algoritmina nopeampi kuin Eratostheneen seula, mutta laskujen laskeminen käsityönä on paljon työläämpää. Vaiheet ovat seuraavat:

1. kirjoita luonnolliset luvut 1 … n² neliönmuotoiseen taulukkoon
2. poista taulukosta muota i + j + 2ij olevat luvut, missä i ja j ovat ruutujen sarake- ja rivi-indeksit,

i ja j ovat luonnollisia lukuja, 1 ≤ i ≤ j, i + j + 2ij ≤ n (kuva 6, vasen)

• kerro kukin jäljellä oleva luku kahdella ja lisää 1

Satataulusta saadaan tällä tavalla lukua 200 pienemmät parittomat alkuluvut (kuva 6, oikea), vastaavasti n²-taulusta lukua 2n + 2 pienemmät. [12]

Muitakin alkulukuja tuottavia algoritmeja on olemassa: [13], [14], [15]. On myös polynomeja, joiden useat arvot ovat alkulukuja [16], esimerkiksi:

         n² – n + 41, kun 0 ≤ n ≤ 39.

Alkulukujen ominaisuuksia

Lukuteorian kannalta alkulukujen tärkein ominaisuus on se, että jokainen jaollinen luonnollinen luku voidaan esittää alkulukujen tulona järjestystä vaille yksikäsitteisesti, esimerkiksi

         6 = 2 · 3, 60 = 2 · 2 · 3 · 5 ja 54 321 = 3 · 19 · 953.

 Tulos on niin merkittävä, että sitä sanotaan aritmetiikan peruslauseeksi.

Alkuluvut esiintyvät myös Goldbachin otaksumassa, jonka mukaan jokainen kolmea suurempi parillinen luku on kahden alkuluvun summa [17], esimerkiksi

         12 = 5 + 7 tai 12 345 678 = 31 + 12 345 647.

 Tämä on Eulerin esittämä muoto otaksumasta. Sitä ei ole todistettu. Alun perin Goldbach muotoili otaksuman niin, että jokainen kahta suurempi kokonaisluku on kolmen alkuluvun summa; silloin myös lukua 1 pidettiin alkulukuna [18]. Viittä suuremmat parittomat luvut voidaan esittää vastaavasti kolmen alkuluvun hajotelmina:

         13 = 3 + 5 + 5 tai 11 111 = 41 · 271 = 5 + 19 + 11 087.

Tämä on todistettu [19], [20].

Vierekkäisiä alkulukuja on vain yksi pari: 2 ja 3. Tämä on ilmeistä, sillä kaikki muut alkuluvut ovat parittomia, joten muiden peräkkäisten alkulukujen välissä on aina vähintään yksi jaollinen luku. Jos näitä on vain yksi, sanotaan, että alkuluvut ovat alkulukukaksosia. Alussa alkulukukaksosia usein:

         3 ja 5, 5 ja 7, 11 ja 13 sekä 17 ja 19.

Myöhemmin ne käyvät yhä harvinaisemmiksi. Ei tiedetä, onko alkulukukaksosia äärettömän monta paria. Nykyään suurin tunnettu alkulukukaksospari [21] on

         2996863034895 × 2^1290000 ± 1.

Sen kymmenjärjestelmäesityksessä on yli 380 000 numeroa.

Muitakin alkulukupareja on nimetty: serkkualkulukujen erotus on 4; ”sexy primes” ei viittaa seksiin, vaan siihen, että niiden erotus on kuusi, esimerkiksi 29 ja 23; ehdoton alkuluku (engl. absolute) on alkuluku, kirjoitettiinpa sen numerot missä järjestyksessä tahansa, esimerkiksi 199, 919, 991. Enemmän hupipuolelle kuin matematiikkaan kuuluvat sellaiset nimitykset kuin pedon alkuluku, (engl. beastly prime) esimerkiksi 700666007; syklinen alkuluku (engl. circular prime), esimerkiksi 1193, 1931, 9311, 3119; kaarevanumeroinen alkuluku (engl. curved-digit prime), joka muodostuu numeroista 0, 6, 8 ja 9; pyyhittävä alkuluku (engl. deletable prime), josta voidaan poistaa mikä tahansa numero niin, että tulos on edelleen alkuluku, esimerkiksi 1987; reikäinen alkuluku (engl. holey prime), joka koostuu ”reiällisistä” numeroista 0, 4, 6, 8 ja 9; nollallinen alkuluku (engl. naughty prime), joissa on enemmän nollia kuin muita numeroita, esimerkiksi 1 000 303 (huomaa sanaleikki ”naught” = nolla, ei mitään, vaikka sanalla ”naughty” on tavanomaisesti muu merkitys) sekä tasannealkuluku (engl. plateau prime), jonka keskimmäiset numerot ovat samoja ja reunimmaiset taas keskenään samoja, mutta lukuina pienempiä kuin keskimmäiset, esimerkiksi 1777771. Vaikka näistä monet viittaavat vain luvun numeroesityksen ulkoiseen muotoon eivätkä siten ehkä sinänsä edistä lukuteorian tai muunkaan matematiikan oppimista, niin niillä ja vastaavilla ideoilla saattaa olla pedagogista merkitystä opetuksen lomaan sijoitettuina kevennyksinä tai luovuuden harjoittelussa. [22]  

Peräkkäisten alkulukujen väli kasvaa keskimäärin lukujen kasvaessa. Alkulukuja on siis yhä harvemmassa. Satunnaisesti valittu positiivinen kokonaisluku n on alkuluku todennäköisyydellä 1 / ln(n). Esimerkiksi kun n on noin 10 000, keskimäärin joka yhdeksäs (≈ 1 / 9,21 ≈ 0,109) luku on alkuluku, kun taas arvolla n ≈ 1 000 000 000 noin joka kahdeskymmenes (≈ 1 / 20,72 ≈ 0,048). Peräkkäisistä jaollisista luvuista muodostuvat välit voivat olla rajattoman pituisia, sillä esimerkiksi n – 1 lukua n! + 2, n! + 3, n! + 4, … , n! + n ovat kaikki jaollisia.

Vähänkin suuremmilla n:n arvoilla nämä välit ovat kaukana luonnollisten lukujen jonossa, sillä esimerkiksi kun n = 10, niin n! on miljoonia, ja kun n = 20, niin n! on triljoonia (10¹⁸). Edellä olevan lausekkeen takaaman, jaollisista luvuista muodostuvan välin pituus ei ole kuin 9 edellisessä tapauksessa ja 19 jälkimmäisessä. Joka tapauksessa tällaisen välin pituus kasvaa rajatta n:n mukana. Luonnollisten lukujen joukossa on esimerkiksi vähintään miljoona peräkkäistä jaollista lukua, kun n = 1 000 001. Tällaiset luvut ovat kovin suuria, mutta nykylukion arkipäivää. Esiintyihän välin ensimmäinen luku ylioppilaskirjoitusten matematiikan kokeen tehtävässäkin syksyllä 2020 [23].

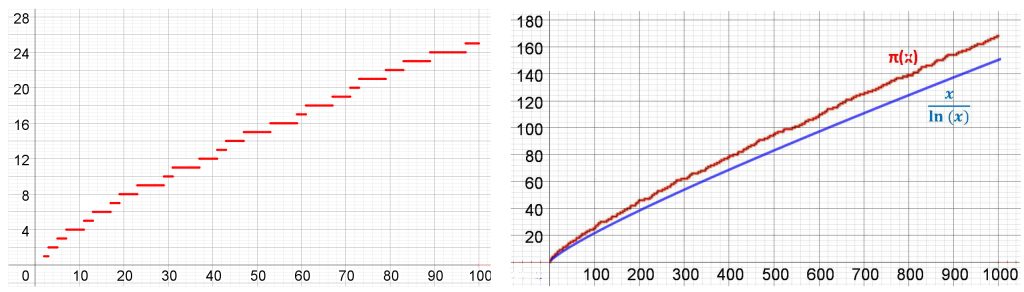
Lukua n pienempien alkulukujen määrä π(n) kasvaa suhteellisen säännöllisesti likimäärin verrannollisena luvun n ja sen luonnollisen logaritmin osamäärään [24] (kuva 7). Säännöllisyyttä näkyy myös siinä, että jotkut alkuluvut asettuvat jonoiksi, kun alkuluvut sijoitetaan koordinaatistoon spiraaliksi, esimerkiksi Ulamin spiraali (kuva 8). Muita vastaavia kuvallisia esityksiä ovat Sacksin [25], [26] ja fyllotaksinen [27] spiraali.

Viestin salaaminen

Suuria alkulukuja käytetään sähköisten viestien salaamiseen ja sähköisten allekirjoitusten aitouden varmistamiseen. Esimerkiksi RSA-salakirjoituksen perusidea on kahden hyvin suuren, yli satanumeroisen alkuluvun tulo. Tähän perustuva avain voidaan julkaista, koska tekijöihin jakaminen vie vuosikymmeniä supertietokoneiltakin, jos tekijät on hyvin valittu. Jaollisuustietoon perustuvat salaus- ja purkuavaimet pidetään vain viestin lähettäjän ja vastaanottajan tiedossa. [28]

Idean ymmärtämistä voi ehkä auttaa luku 50! + 1. Jaoin sen ensin pienillä (!) alkulukutekijöillään

         149, 3 989 ja 74 195 127 103.

Sittenkin osamäärä

         689 682 465 466 631 337 960 345 542 732 568 061 755 962 721 847

on liian suuri taskulaskimille, Geogebralle ja useimmille verkossa oleville tekijöihinjakolaskimillekin. Kuitenkin esimerkiksi Prime Factors Calculator for Very Big Numbers [29] pystyi yrittämään sen tekijöihinjakamista. Se pääsi testaamisessa lähes 160 miljardiin yhden tunnin aikana (kuva 9), kun tarve olisi ollut lähes 7 biljoonaa eli yli nelikymmenkertainen, sillä pienempikin tekijöistä on kolmetoistanumeroinen

         6  854  870  037  011

Huonossa tapauksessa, jossa tekijät olisivat olleet luvun neliöjuuren eli kvadriljoonan kertaluokkaa, aikatarve olisi ollut biljoonakertainen. Kotitietokoneeni olisi siis tarvinnut laskemiseen tällä ohjelmalla vähintään vuorokausia, huonossa tapauksessa miljoonia vuosia. Oikeiden matematiikkatyövälineiden laskentanopeus on kuitenkin omaa luokkaansa, sillä esimerkiksi Mathematica jakaa luvun tekijöihin käytännöllisesti katsoen viipeettä [30].

Tosisuurten, monisatanumeroisten salakirjoitusavainten selvittäminen on kuitenkin aikaavievää puuhaa supertietokoneillekin. Se vie vuosia. Koodin murtaminen ei kannata, sillä viestin sisältämä tieto on silloin jo vanhentunut. Eikä kyse ole aina vain muutamista vuosista. Supertietokoneeltakin voisi viedä miljardeja vuosia vain 256-bittisiin eli 78-numeroisiin lukuihin perustuvan koodin avaamiseen. Salausavaimet voivat olla käytännössä vielä paljon pitempiä. Näin salattuja viestejä käytät todennäköisesti päivittäin, kun käytät luottokorttia tai verkkopankkia. [31]

Lähteitä ja lisää lukemista

[1] Kouvolan kaupungin Liikkuva koulu -hankkeen Pedanet-materiaali: Lukujen hajottaminen osoitteessa [2] Wikipedia-artikkeli Greatest known prime osoitteessa https://en.wikipedia.org/wiki/Largest_known_prime_number

[3] Wikipedia-artikkeli Perfect number osoitteessa https://en.wikipedia.org/wiki/Perfect_number

[4] Kivelä, Simo: M niinkuin matematiikka osoitteessa http://matta.hut.fi/matta/isom/isom.pdf#page.26

[5] Wikipedia-artikkeli Divisibility rule osoitteessa https://en.wikipedia.org/wiki/Divisibility_rule

[6] Anni Lampisen sähköpostiviesti 29.1.2023

[7] Rita Järvisen sähköpostiviesti 7.2.2023

[8] Erkki Luoma-ahon sähköpostiviesti 7.2.2023

[9] Korkeamäki, Kalle (2019): Alkulukukaksosten karakterisoinnista, s. 7. Pro gradu -tutkielma, Tampereen yliopisto, Informaatioteknologian ja viestinnän tiedekunta. Saatavissa osoitteesta https://trepo.tuni.fi/bitstream/handle/10024/115639/KorkeamakiKalle.pdf?sequence=2

[10] Maynard, James (2022): Counting primes, s. 2. Esitelmä kansainvälisessä matemaatikkojen verkkokonferenssissa 2022. Preliminary version, to appear in Proc. Int. Cong. Math. 2022, Vol. 1. Saatavissa osoitteesta https://www.mathunion.org/fileadmin/IMU/Prizes/Fields/2022/jm.pdf

[11] Geogebra-materiaali Eratostheneen seula osoitteessa https://www.geogebra.org/m/sazjyjpb

[12] Wikipedia-artikkeli Sieve of Sundaram osoitteessa https://en.wikipedia.org/wiki/Sieve_of_Sundaram

[13] Wikipedia-artikkeli Generation of primes https://en.wikipedia.org/wiki/Generation_of_primes

[14] Wikipedia-artikkeli Sieve of Atkin osoitteessa https://en.wikipedia.org/wiki/Sieve_of_Atkin

[15] Wikipedia-artikkeli Wheel factorization osoitteessa https://en.wikipedia.org/wiki/Wheel_factorization

[16] Prime-Generating Polynomial osoitteessa https://mathworld.wolfram.com/Prime-GeneratingPolynomial.html

[17] Lehtonen, Teemu (2004): Alkulukujen teoriaa ja Goldbachin otaksuma, s. 36–42. Pro gradu -tutkielma, Matematiikan, tilastotieteen ja filosofian laitos, Tampereen yliopisto. Saatavissa osoitteesta https://trepo.tuni.fi/bitstream/handle/10024/91709/gradu00319.pdf?sequence=1&isAllowed=y

[18] Wikipedia-artikkeli Goldbach’s conjecture osoitteessa [19] Wikipedia-artikkeli Goldbach’s weak conjecture osoitteessa [20] Ernvall-Hytönen, Anne-Maria: Suuria ja vielä suurempia lukuja. Solmu-lehti 2/2022 s. 1, osoitteessa https://matematiikkalehtisolmu.fi/2022/2/paak_2_22.pdf

[21] Largest known twin primes osoitteessa https://googology.fandom.com/wiki/Largest_known_twin_primes

[22] Alec Wilkinson, Alec (2015): The Pursuit of Beauty. The New Yorker 2.2.2015. Saatavissa osoitteesta https://www.newyorker.com/magazine/2015/02/02/pursuit-beauty

[23] Ernvall-Hytönen, Anne-Maria: Alkulukuja ja yhdistettyjä lukuja – ylioppilastehtävä yleistyksineen. Matematiikkalehti Solmu 3/2022, s. 16–17, osoitteessa https://matematiikkalehtisolmu.fi/2020/3/alkulukuja_ja_yhdistettyja.pdf

[24] Shalit, Ehud de (2018): Prime Numbers – Why are They So Exciting? osoitteessa https://kids.frontiersin.org/articles/10.3389/frym.2018.00040

[25] Ross, Michael M.: The Sacks Number Spiral osoitteessa http://www.naturalnumbers.org/sparticle.html

[26] Barron, Lola (2021): Prime Numbers – What We Know. Saatavissa osoitteesta https://tomrocksmaths.com/2021/07/07/prime-numbers-what-we-know-1/

[27] Prime phyllotaxis sprirals osoitteessa https://maxwelldemon.com/2012/03/18/prime-phyllotaxis-spirals/

[28] Sipola, Tapani (2017): RSA-salausmenetelmä. LuK-tutkielma, Matemaattisten tieteiden laitos, Oulun yliopisto, osoitteessa http://jultika.oulu.fi/files/nbnfioulu-201710193003.pdf

[29] Prime Factors Calculator for Very Big Numbers osoitteessa https://www.random-science-tools.com/maths/prime-factors.htm

[30] Simo Kivelän sähköpostiviesti 9.2.2023

[31] Tomlinson, Zachery (2018): The Incredible Importance of Prime Numbers in Daily Life osoitteessa https://interestingengineering.com/science/the-incredible-importance-of-prime-numbers-in-daily-life