Lukusuoramallin ja pinta-alamallin yhtäaikainen hyödyntäminen murtolukujen yhteydessä
Alakoulun matematiikan oppikirjojen kuvallinen tuki murtolukujen opetuksessa vaihtelee suuresti eri luokka-asteilla. Mitä vanhempia oppilaat ovat, sitä vähemmän näkyy kuvallisia representaatioita. Myös lukusuoramallin hyödyntäminen tuntuu vähenevän sitä mukaa mitä vanhemmista oppilaista on kyse. Tutkimuksessa keskitytään erityisesti lukusuoramallinnuksen hyödyntämiseen muiden representaatioiden kuten symbolimuotoisen murtoluvun tai pinta-alamallin kanssa. Tutkimuksessa esitellään muokattu lukusuoramalli, joka on kehitetty tukemaan murtolukujen suuruuden hahmottamista hyödyntäen oppilaille tuttuja representaatioita.
Murtoluvuilla ($n/m, m ≠ 0$ ja $m, n$ $ \in $ Z) on useita eri representaatioita. Murtoluvuille käytetään usein symbolimuotoista esitystä mutta oppikirjoissa näkee myös pinta-ala- ja janamallin ja lukusuoran hyödyntämistä. Vaikka kullakin esitysmuodolla on omat hyvät ja huonot puolensa, käyttämällä useita eri representaatioita luodaan oppilaille vankka pohja ymmärtää murtolukukäsite laajasti. Esimerkiksi konkreettisilla murtokakkupaloilla voidaan hyvin havainnollistaa murtolukujen välistä yhteen- ja vähennyslaskua, jolloin oppilaille syntyy tarve yhteisen nimittäjän löytämiseksi, mitä taas symbolimuodossa esitetyt murtolukulaskut eivät tee (Cramer & Wyberg 2009). Havainnollistamisvälinettä tai representaatiota valittaessa täytyy kuitenkin huomioida oppilaiden tietotaso; se, mikä näyttäytyy opettajalle hyödyllisenä representaationa, ei ole välttämättä oppilaille hyödyllinen vaan voi jopa mahdollistaa virhekäsitysten muodostumisen. Myös opettajilla saattaa olla rajoittunut käsitys siitä, minkälainen representaatio toimii milloinkin parhaiten tai he saattavat jopa suosia vain yhtä tyyliä.
Kuvallinen esitysmuoto voidaan luokitella sen mukaan, miten se toimii tehtävän tukena: kuva voi olla koristekuva, esittävä kuva, järjestelmäkuva tai informatiivinen kuva (Carney & Levin 2002). Esittävä kuva saattaa kuvata koko ongelman tai vain osan siitä, järjestelmäkuva tarjoaa apua ratkaisuproseduuriin ja informatiivinen kuva tarjoaa ratkaisun kannalta oleellista lisäinformaatiota eli ongelma perustuu kuvaan. Kuvan aktiivinen hyödyntäminen voi johtaa sisäiseen ristiriitaan, mikä kuitenkin on merkityksellinen ja hyödyllinen vieden ratkaisua eteenpäin. (Elia & Philippou 2004.) Tällainen sisäinen ristiriitatilanne on esimerkiksi sellainen, missä laskemalla saatu vastaus ja piirroksella tuotettu vastaus poikkeavat toisistaan. Kuvan hyödyntäminen saattaa olla keskeinen osan ongelmanratkaisuprosessia. Boonen, Schoonenboomen ja Jollesin (2016) tutkimuksessa kuvat luokiteltiin kahteen ryhmään: kuvalliseen esitykseen ja aritmeettiseen esitykseen. Kuvallinen esitys saattoi kuvata tehtävässä annetun henkilön tai asian kuitenkaan ilmaisematta asioiden välisiä suhteita. Aritmeettinen kuva taas tukee laskun suorittamista, esimerkiksi kuvaa mehutiivisteen ja veden määrän välistä suhdetta. Jos ratkaisija hyödynsi vain aritmeettista esitystä ennen kuin oli ymmärtänyt tehtävän, johti tämä usein virheelliseen ratkaisuun. Kuvallista esitystä tulisikin käyttää ensin ongelman ymmärtämiseen ja vasta sen jälkeen tulisi hyödyntää aritmeettista esitystä varsinaisen laskemisen tukena. Esimerkiksi luokanopettajaopintojen valintakokeen matemaattis-luonnontieteellisen ajattelun testissä, MALU-testissä, olleessa tehtävässä kuvan piirtäminen auttoi oleellisesti ratkaisemaan tehtävän oikein. Moni laskija sortui poimimaan luvut tehtävänannosta ja kertomaan ne keskenään saadakseen mokkapalojen lukumäärän. Kyseisellä tehtävällä saatiin seulottua ne hakijat, jotka tukeutuvat piirtämiseen ratkaisukeinona.
Juha-eno leipoo pellillisen herkullisia mokkapaloja jalkapalloturnauksen myyjäisiin. Hän leikkaa valmiiseen pellilliseen pitkittäin kolme viiltoa ja poikittain neljä viiltoa. Jos yksi pala maksaa 1,50 €, niin kuinka paljon kassaan kilahtaa rahaa koko mokkapalapellillisen myynnistä? (MALU-2018, osa II)
Dreherin ja Kuntzen (2014) tutkimuksessa tutkittiin sitä, miten saksalaiset opettajat ja opettajaksi opiskelevat hyödyntävät erilaisia representaatioita murtolukujen yhteydessä. Tutkijat totesivat, että sekä opettajien että opetusharjoittelijoiden opetuksessa niin sanottu palkkimalli oli yliedustettuna, vaikka esimerkiksi pitsamallin tai lukusuoran hyödyntäminen olisi toiminut kyseisen tehtävän kohdalla paremmin. Tutkijat toteavatkin, että opettajat tarvitsevat lisää ymmärrystä erilaisten representaatioiden hyödyntämisessä ja kunkin mallin tuomista hyödyistä oppimisen kannalta. Tähän tulisikin kiinnittää huomiota jo opettajankoulutuksessa, jotta opettajilla olisi mahdollisimman laaja repertuaari käytettävinään, ja he pystyisivät tilanteen mukaan siirtymään joustavasti representaatiosta toiseen (Boonen, Reed, Schoonenboom & Jolles 2016).
Silfverberg ja Tuominen (2016) tutkivat sitä, miten sujuvaa murtolukujen eri representaatioiden käyttö ja representaatiosta toiseen siirtyminen on luokanopettajaopiskelijoilla. Tutkimuksen yhtenä tehtävänä oli symbolimuodossa esitettyjen murtolukujen ($\frac{2}{3}$, $\frac{4}{3}$, $\frac{5}{6}$ ja $1\frac{2}{3}$) sijoittaminen lukusuoralle, johon oli valmiiksi annettu lukujen 0 ja 1 paikat. Toisena tehtävänä oli kuvallisessa muodossa annettujen murtolukujen sijoittaminen vastaavalle lukusuoralle (Kuva 1).
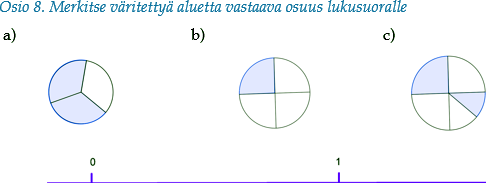
Opiskelijoiden ratkaisuissa ilmeni ongelmia lukujen algebrallisten suhteiden siirtymisessä lukusuoralle, geometrisen mallin pisteiden väliseksi etäisyyksien suhteeksi. Esimerkiksi luku $\frac{1}{4}$ tulkittiin oikein pienemmäksi kuin luku $\frac{3}{8}$ , jonka paikka lukusuoralla vastasi kuitenkin tulkintaa $2\cdot\frac{1}{4}$. (Silfverberg & Tuominen 2016.) Tehtävien joukosta puuttui kuitenkin kokonaan tehtävä, jossa myös lukusuoran kokonaiset olisi ilmaistu numerosymbolin sijaan kuvallisella mallilla.
Oppikirjoissa lukusuora esitetään yleensä annettuna lukuvälinä 0–1 tai 0–x, kuitenkin niin, että kokonaiset kuvataan lukuna, ei pinta-alapiirroksena. Saattaa jopa olla niin, että kullekin nimittäjälle on esitetty oma lukusuoransa (Kuva 2). Tämä altistaa virhekäsitykselle, että esimerkiksi viidesosat olisivat omalla lukusuorallaan ja kahdeksasosat omallaan. Tämä luo pirstaleista kuvaa luvuista: Luonnollisten lukujen lukusuora ei linkity murtolukujen yhteydessä esitettyyn lukusuoraan.
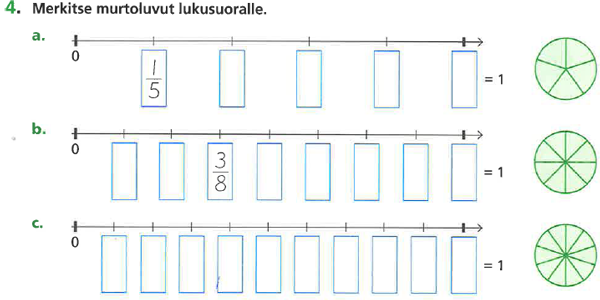
Yllä olevan kuvan (Kuva 2) kaltaiset tehtävät saattavat tukea virhekäsitystä, että seuraava murtoluku saadaan selville luettelemalla. Kuvan 2 vahvuudeksi tulkitsen kuitenkin sen, että yksi kokonainen esitetään myös pinta-alamallina. Jos kohdat a) ja c) olisivat peräkkäin, oppilas saattaisi helpommin huomata, että 1/5 = 2/10. Alla olevan kuvan (Kuva 3) vahvuutena on pinta-alamallien hyödyntäminen murtolukujen suuruusvertailussa ja se, että annettu lukuväli on jotain muuta kuin väli 0–1. Linkitys lukusuoralle olisi vahvempi, jos myös lukusuoralle merkityt luvut olisivat pinta-alamallein kuvatut.
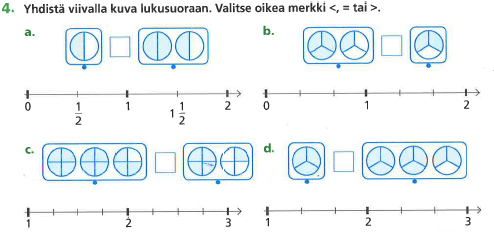
Lukusuora & pinta-ala -representaatio
Miten eri representaatioita kannattaisi käyttää? Minulla oli tilaisuus keskustella kreikkalaisen matematiikan oppimisen tutkijan Xenia Vamvakoussin kanssa lyhyt tuokio väitöskirjatyöhöni liittyen ja hän ehdotti minulle, että hyödyntäisin lukusuoramallia ja kuvallista mallia yhtä aikaa. Tästä innostuneena olen kehitellyt murtolukujen havainnollistusta eteenpäin. Pinta-alamallin käyttäminen mahdollistaa pinta-alojen fyysisen koon vertailun. Piaget (1966) kuvaa lapsen lukukäsityksessä vaihetta, jossa kahteen jonoon asetellaan yhtä monta marmorikuulaa. Kun toinen jono levitetään laajemmalla alueelle, on lapsen mielestä jonossa enemmän kuulia kuin tiiviimmin astellussa jonossa. Vaikka jonojen kappalemäärät laskettiin ennen uudelleen asettelua ja lapsi tiesi, että kummassakin oli sama määrä kuulia, niin silti jonon fyysinen koko ajoi lukumäärän ohi. Sama havainto tehtiin tilavuuden yhteydessä. Saman vesimäärän kaataminen erimuotoisiin astioihin saa lapsen luulemaan, että vesimäärä muuttuu. Lapset kiinnittävät huomiota vesipatsaan korkeuteen enemmän kuin astian pohjan kokoon luullen, että korkeammassa astiassa on enemmän vettä. Lapsilla on siis taipumusta vertailla asioiden fyysisistä kokoa keskenään. Kuvaamalla murtoluku myös pinta-alamallilla, voidaan hyödyntää oppilaan taipumusta tukeutua luvun fyysiseen kokoon. Pinta-alamallina kuvattu luku on helpompi asettaa lukusuoralle kuin symbolimuodossa esitetty murtoluku.
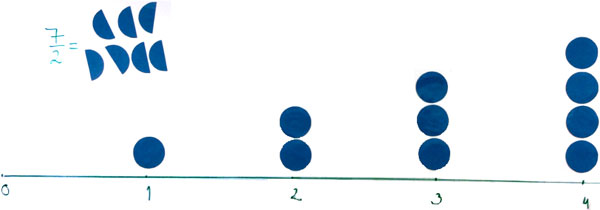
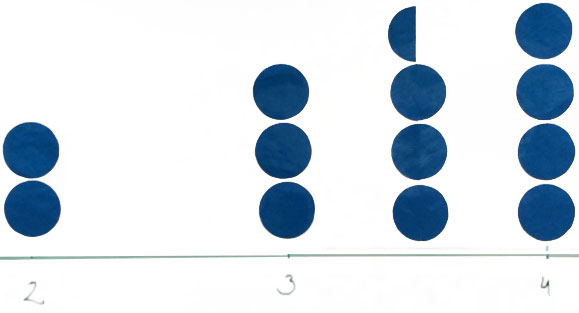
Lähtökohtana on linkittää oppilaille luonnollisten lukujen kautta tuttu lukusuoramalli murtolukumalliin, joka nojaa osa kokonaisesta -ajatteluun. Esimerkkiin on tietoisesti otettu mukaan sekalukuja. Lukusuoralle on merkitty luvut 0–4 sekä symbolimuodossa että kokonaisina ympyröinä: luvun 1 kohdalla niitä on yksi kappale, luvun 2 kohdalla kaksi kappaletta ja lopulta luvun neljä kohdalla neljä kappaletta. Mielestäni tämä on se kohta, mikä oppilailta puuttuu: oppilaat eivät ymmärrä, että lukusuoran luku 1 tarkoittaa yhtä kokonaista ja vastaavasti luku 2 tarkoittaa kahta kokonaista, ellei opettaja sitä korosta opetuksessaan.
Symbolimuodossa ilmaistu murtoluku 7/2 kuvataan ensin pinta-alamallina; seitsemän kappaletta puolikkaita, joista saadaan kolme kokonaista ja puolikas. Nyt on helppo pinta-aloja vertaamalla löytää oikea kohta lukusuoralta vastaamaan murtolukua 7/2 (Kuva 4 ja Kuva 5).
Kansainvälisissä tutkimuksissa nousee esille käsite equal fractions, jota suomalaisissa oppikirjoissa ei juurikaan oteta esille. Vastaavasti taas suomalaisissa oppikirjoissa keskitytään mekaaniseen laventamiseen ja supistamiseen, joista kummallekaan en ole löytänyt omaa käsitettä kansainvälisiin tutkimuksiin tutustuessani. Oleellisin piirre se, että murtoluvun suuruus ei muutu, tuntuu hautautuvan mekaaniseen suorittamiseen. Esimerkiksi luku puoli voidaan esittää murtolukumuodossa, vaikka kuinka monella eri tavalla mutta ne kaikki osoittavat kuitenkin lukusuoralla samaan kohtaan, mikä voidaan havaita esimerkiksi Lukusuora & pinta-alamallin avulla.
Edellä esitettyä Lukusuora & pinta-ala –representaatiota on hyödynnetty väitöskirjaan tähtäävässä interventiotutkimuksessa, luokanopettajaopiskelijoiden matematiikan kurssilla ja Joustava matematiikka -verkkokurssin esimerkkivideoilla.
Perusopetuksen opetussuunnitelman perusteissa sanotaan, että oppilaille tarjotaan välineitä oppimisen tueksi ja luodaan mahdollisuuksia oivaltaa ja ymmärtää itse. Matematiikkaa opiskellaan oppimisympäristössä, jossa konkretisointi ja välineet ovat keskeisessä asemassa. Välineet tulee olla helposti saatavilla (Opetushallitus 2014). Oppilaalla tulisikin olla mahdollisuus hyödyntää sitä välinettä tai representaatiota mikä kulloinkin tuntuu hänelle sopivimmalta. Symbolimuodossa annettu tehtävä tulisi siksi saada ratkaista esimerkiksi välinein tai kuvituksen avulla.
Lähteet
Boonen, A., Reed, H., Schoonenboom, J. & Jolles, J. 2016. It´s not a math lesson–we´re learning to draw! Teachers´ use of visual representations in instructing word problem solving in sixth grade of elementary school. Frontline Learning Research, 4(5), 55–82.
Cramer, K. & Wyberg, T. 2009. Efficacy of Different Concrete Models for Teaching the Part-Whole Construct for Fractions. Mathematical Thinking and Learning, 11, 226–257.
Dreher, A. & Kuntze S. 2014. Teachers´ professional knowledge and noticing: The case of multiple representations in the mathematics classroom. Educational Studies in Mathematics, 88, 89–114.
Elia, I. & Philippou, G. 2004. The functions of pictures in problem solving. Proceedings of the 28th Conference of the International Group for the Psychology of Mathematics, 2, pp 327–334.
Opetushallitus. 2014. Perusopetuksen opetussuunnitelman perusteet 2014. ss. 130, 236.
Piaget J. 1966. La Psychologie de l´Enfant. Käännetty teos (1977) Lapsen psykologia. Helsinki: Gummerus. 95-96.
Silfverberg, H. & Tuominen, A. 2016. Murtoluvun ja lukusuoran pisteen välinen vastaavuus – tyypillisimpiä virheitä luokanopettajaopiskelijoiden suorituksissa. Teoksessa H. Silfverberg & P. Hästö (Eds.), Matematiikan ja luonnontieteiden opetuksen tutkimusseuran tutkimuspäivät 2015 Annual symposium of the finnish mathematics and science education research association 2015 (ss. 133–142). Retrieved from http://www.protsv.fi/mlseura/julkaisut/MALU2015_Final.pdf ISBN 978-952-93-8233-0.
Kiviluoma, P., Nyrhinen, K., Perälä, P., Rokka, P., Salminen, M. & Tapiainen, T. 2016. Tuhattaituri 4b. Helsinki: Otava.
Aloituskuva: Michael Glass / Unsplash







